7. Гидравлический расчет отрытых каналов при равномерном движении жидкости

Открытыми каналами называют безнапорные водотоки. В отличие от рассмотренных выше случаев напорного движения жидкости, при котором живое сечение потока совпадало с поперечным сечением канала (трубопровода), в случае безнапорного движения лишь часть периметра потока ограничена твердой поверхностью и всегда имеется свободная поверхность - граница между газом и жидкостью. Отсюда вытекает важное, следствие - давление на свободной поверхности жидкости в открытом канале можно принять постоянным вдоль потока.

В этом случае движение жидкости происходит только за счет силы

тяжести и требует наличия геодезического уклона местности либо разности уровней

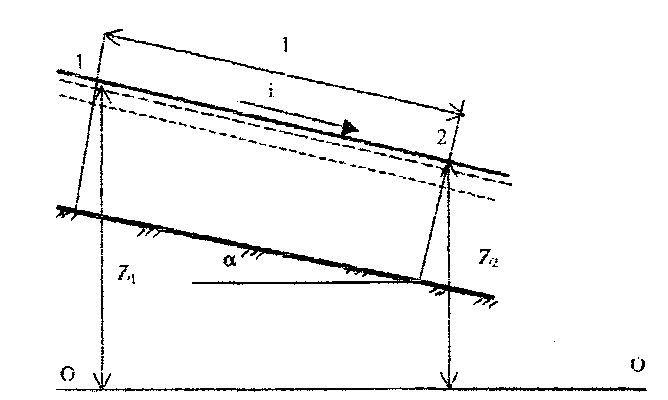
жидкости в начальном и конечном сечениях сечениях

канала (рис.7.1). При этом, если размеры и форма живого сечения потока, шероховатость стенок канала, канала,

Рис.7.1. Продольное сечение

безнапорного потока

гидравлический уклон и средняя скорость

движения жидкости по длине канала остаются неизменными, то такое

движение называют равномерным движением жидкости.

При равномерном движении глубина потока, h остается постоянной по всей длине какала.

Очевидно, что вся энергия, которую получает поток за счет работы

силы тяжести, расходуется на преодоление сил трения, создающих

сопротивление движению, а кинетическая энергия потока не изменяется

вдоль течения. Глубина, при которой в призматическом канале имеет место равномерное движение, называется нормальной и обозначается через h₀.

7.1. Основные расчетные зависимости и типы задач

Из уравнения Д. Бернулли, записанного для двух живых сечений

потока относительно плоскости сравнения О-О, следует, что

(7.1)

откуда (7.2)

При равномерном движении жидкости в канале гидравлический уклон равен уклону дна канала.

Основной расчетной зависимостью для каналов является формула Шсзи для определения средней скорости течения:

(7.3)

где V- средняя скорость движения жидкости, м/с;

С- коэффициент Шези, м^0,5/с;

R - гидравлический радиус, вычисляемый по формуле (4.10), м

 - площадь живого сечения потока, м²;

- смоченный периметр, м;

i - гидравлический уклон.

Большинство формул для определения коэффициента Шези С представляют собой эмпирические зависимости, действительные лишь для определенных значений скоростей и гидравлических радиусов.

Наиболее удобной и часто применяемой является формула Маннинга:

(7.4)

где n- коэффициент шероховатости, зависящий от материала стенок канала и качества поверхности. Значения коэффициентов шероховатости для ряда характерных поверхностей приведены в приложении 11 пособия.

Расход воды определяется по формуле:

(7.5)

где - расходная, характеристика (модуль расхода).

В свою очередь величина

(7.6)

называется скоростной характеристикой или модулем скорости.

Модуль расхода (расход при уклоне, равном единице) и модуль скорости ( скорость при уклоне, равном единице) вводятся для упрощения гидравлического расчета каналов и могут быть вычислены предварительно по известным размерам и форме сечения канала или взяты из справочной литературы.

Большое значение имеет правильный выбор скорости движения воды в канапе. Слишком малые скорости требуют большого сечения канала и способствуют его заилению, Чрезмерно большие скорости могут вызвать размыв и разрушение стенок. Предельная минимальная назначаемая скорость движения воды в канале называется незаиляющей скоростью (V_незаил). а предельная максимальная скорость - неразмывающей скоростью (V_неразм).Необходимо, чтобы скорость воды в канале V была

Необходимо, чтобы скорость воды в канале V была

V_незаил < V < V_неразм (7.7)

Допускаемая неразмывающая скорость зависит от рода грунта, типа облицовки канала и глубины воды в нем и может быть определена, например, по формуле И.И.Леви,

, (7.8)

где d - средний диаметр частиц, слагающих русло.

Допускаемая незаиляющия скорость воды в канале зависит, главным образом, от характера взвешенных в воде наносов и определяется, например, по формуле Е.А. Замарина;

(7.9)

где  - мутность потока, кг/м³;

W- средневзвешенная гидравлическая крупность наносов, м/с;

М - коэффициент, принимаемый равным W при W>0,002 м/с и равным 0,002 при W<0,002 м/с.

Форма поперечного сечения канала выбирается в зависимости от его размеров, характера грунта, облицовки, назначения и т.д. Наиболее часто используются каналы трапецеидального сечения, для которых

, (7.10)

, (7.11)

Рис.7.2. Канал трапецеидального сечения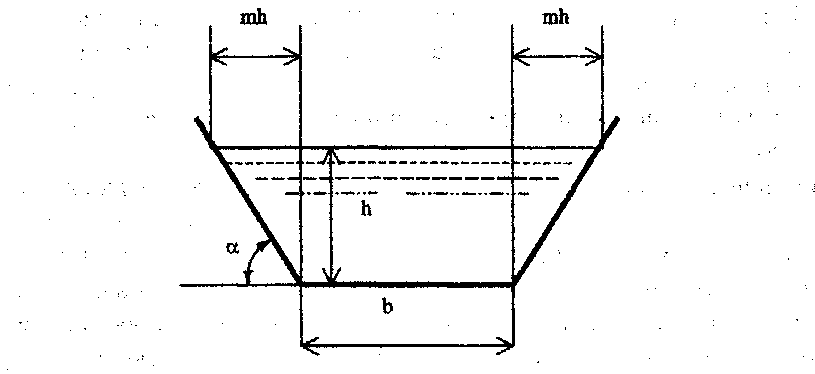

г де b - ширина канала по дну, м; h -глубина наполнения канала, м; т =ctg  -коэффициент откоса канала (рис.7.2).

- 175 -

Коэффициент откоса выбирается из условий устойчивости в зависимости от качества грунта и способа крепления откоса.

Сечение канала, у которого при заданной площади живого сечения потока , уклоне i и заданной шероховатости стенок расход оказывается наибольшим, называется гидравлически наивыгоднейшим сечением.

При проектирований трапецеидальных каналов отношение ширины

канала по дну к глубине в некоторых случаях может быть принято гидравлически наивыгоднейшим, определяемым по формуле

(7.12)

Однако такое сечение не всегда оказывается экономически и технологически наивыгоднейшим, поэтому на практике в основу выбора значения , если нет других ограничивающих условий, должна быть положена экономичность поперечного профиля с точки зрения объема и способа выполнения работ,

Представленные выше зависимости могут быть использованы при расчете движения воды и других жидкостей.

Этим же зависимостям подчиняется и движение жидкости в канализационных, дренажных и водосточных трубах при неполном заполнении поперечного сечения. Для облегчения их расчетов широко применяются графики средней скорости и расхода в зависимости от степени заполнения поперечного сечения трубы.

Основные типы задач гидравлического расчета трапецеидальных каналов при равномерном движении воды сводятся к следующим.

Задача типа 1. Определить гидравлический уклон i, если заданы величины расхода Q, нормальной глубины h, ширины канала по дну b, коэффициента шероховатости п и заложения откоса m?,

Задача решается прямой подстановкой в формулу Шези, записываемую в виде -

, (7.13)

где  - площадь живого сечения вычисляется но формуле (7.10), м²;

- смоченный периметр вычисляется по формуле (7.11), м;

R - гидравлический радиус, м;

С- коэффициент Шези_у м^0,5 /с.

Задача типа 2. Определить расход воды в канале Q, если заданы величины гидравлического уклона i, нормальной глубины h_ь ширины канала по дну b, коэффициента шероховатоcnи п и заложения откоса т.

Задача решается аналогично предыдущей е помощью формулы Шези, записанной в виде

, (7.14)

Задача типа 3. Определить ширину канала по дну b, если заданы величины гидравлического уклона i, расхода воды в канале Q, нормальной глубины h, коэффициента шероховатости п и коэффициента откоса т. Задача решается методом подбора - графически или аналитически с помощью ПЭВМ. Задавая ряд значений b, определяют, как и в задаче 2, расход для каждого задаваемого b и строят график зависимости Q=Q(b), a затем по заданному значению Q_зад определяют искомую ширину канала b_иск (рис7.3,а).

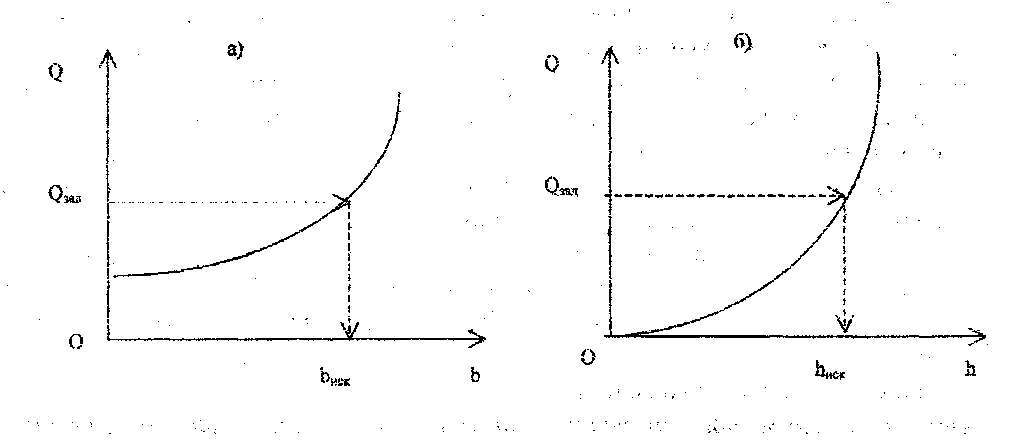
Рис. 7.3. Графическое решение задач 3 и 4 типов

Задача типа 4. Определить нормальную глубину h, если заданы величины

гидравлического уклона i, расхода воды в канале Q, ширины канала но дну b,

коэффициента шероховатости п и коэффициента откоса т.

Задача решается аналогично предыдущей, т.е. задавая ряд значений h,

определяют расход для каждой задаваемой глубины и строят график

зависимости Q=Q(h), а затем по заданному значению Q_зад определяют

искомую глубину h_иск (рис.7.3,б).

Задача типа 5. Определить нормальную глубину h и ширину канала по дну

b, если заданы величины гидравлического уклона i, расхода воды в канале Q,

гидравлически наивыгоднейшей относительной ширины канала по дну

, коэффициента шероховатости п и коэффициента откоса т.

Задача решается в такой последовательности.

Задавая ряд значений h_, находят соответствующие b=_гнh, а затем строят график зависимости Q=Q(h) и по заданному расходу Q_зад определяют искомые h и b.