88.Метод главных компонент.
Позволяет решать несколько задач:
1)Снижение размерности пространства признаков, омывающих объект.
2)Т.к. главные компоненты не коррелированны, то решается ещё задача: построение уравнения регрессии на некоррелированных гл. компонентах.
3)Классиф-я объектов пров-ся:
а)Ранжирование по 1-й из гл. компонент
б)Класс-я в геометрическом пространстве (2-х мерном) в пространстве 2-х гл. компонент.
в) Класс-я в 3-х мерном простр-ве
Осн. алгоритм компонентного анализа.
1)Матрица исх-х данных (n-k)Х
2)Нормирование матрицы Х (для избежания размерных измерений) получаем матрицу Z.
3)Выч-м матрицу парных коэф-в корреляции.R
4) Представление матрицы R в матрицу собственных значений λ на основании решения хар-го уравнения:/R-∆E/=0
5)отыскание для каждого собственного λ не нормированного собственного вектора как решения след-го уравнения(R- λνE)*Vν = 0.
6)Нормировка ненормированных собств.векторов нах-ся след-м образом: Vν = Vν/ (Vνт* Vν)0,5
7)Составление матрицы нормированных собст-х векторов.
8)Вычис-ние матрицы весовых нагрузок гл.компонент: A = V* λ0.5
Вычисление матрицы значений гл. компонент F: F = Z(AT)-1
89.Корреляционный анализ
Иссл-я природу общества, эк-ку необх-мо сч-ся со вз-зью набл-х процессов и явлений. Оценка наиболее существ-ных из них а также воздействие одних фак-ров на др-е явл-ся одной из осн-х задач стат-ки.
Формы проявления вз-зей: 1)Функциональная - величине факторного признака соотв-т одно или неск-ко значений функции; 2)Корреляционная связь – проявляется в среднем для массовых наблюдений, когда заданным значениям зависимой переменной сосотв-т нек-й ряд вероятностных значений независимой переменой.
а)По направ-ям связи м.б . прямым и обратным(“+” или “-”); б)Отн-но ан-з.формы: лин-ным и нел-м; в)Взаимодействующие факторы: связь 2-х приз-ков – парная, более – множ-венная; г)Слабые и сильные связи.
В стат-ке различают след. виды корреляций: 1)Парная корреляция – связь м/у 2-мя признаками; 2)Частная корреляция – зависимость м/у результативном и 1 факторным признаком, при фиксированном значении всех остальных признаков; 3)Множ-ная кор-ция – зав-ть рез-го приз-ка и 2-х или более факторных.
Кор-й анализ имеет своей задачей колич. оценки тесноты связи м/у 2-мя признаками при парной связи и множеством факторных признаков при многофакторной. Теснота связи выр-ся коэф-ом. Основной предпосылкой прим-я кор-го анализа явл-ся необходимость подчинения сов-ти всех факт. и результ. признака k- мерному закону распределения или по крайней мере близость к нему. Если объём иссл-й сов-ти дост. большой то нормальность распределения м.б. подтверждена на осн. расчета и анализа критериев согласия Пирсона.
Парный коэф-т корреляции: ryxi = σyxi/σyσij = (xyср-xсрyср)/Sxj*Sy; где
Sxj = (1/nΣ(xij-xср)2)0.5; Sy = (1/nΣ(yj-yср)2)0.5; tH =( |ρ|/(1- ρ2)0.5)(n-2)0.5
Если расчётное значение больше табличного то связь есть.
МКК.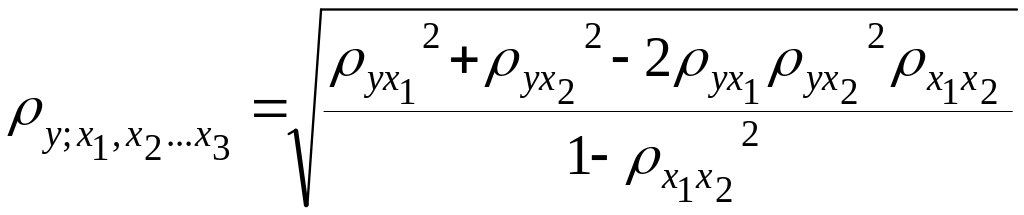
Проверка основывается на F – критерии Фишера.
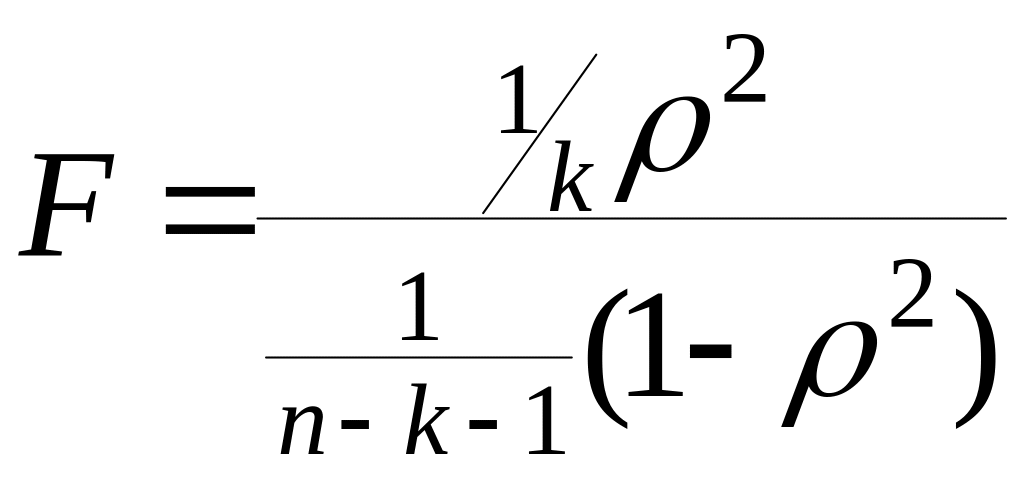
если рассчитанное значение больше табличного то связь есть.
ЧЧК.
Проверяется с помощью t – критерия Стьюдента:
tH =( |ρ|/(1- ρ2)0.5)(n-L-2)0.5, где L – порядок ЧКК.
Если расчетное значение больше табличного то связь есть.