87. Корреляция временных рядов.

При рассмотрении неск-х динамических рядов можно встретить ряды у кот-х колебание уровней взаимообусловлены т.е. возникает необ­ход-ь измерить зависимость м/у рядами динамики или опред-ть на­сколько колебания уровней одного ряда зависит от колебания уровней др. рядов. При корреляции временных рядов нужно учитывать следующие особенности: 1) Во временных может иметь место автокорреляция, корреляц-ый анализ временных рядов прим-ся тогда когда в рядах отсутствует автокорреляция. Вр. ряды не должны сод-ть тенденций, т.е. отдельные уровни должны быть независимыми и нормально распределены. В случаи наличия автокорр-ции м/у уровн-ми вр.ряда она должна быть устранена. Существуют 3 метода исключения: 1) метод авторегрес-х преобраз-й – опред-т тесноту связи м/у отклонениями от тенденций двух врем-х рядов: 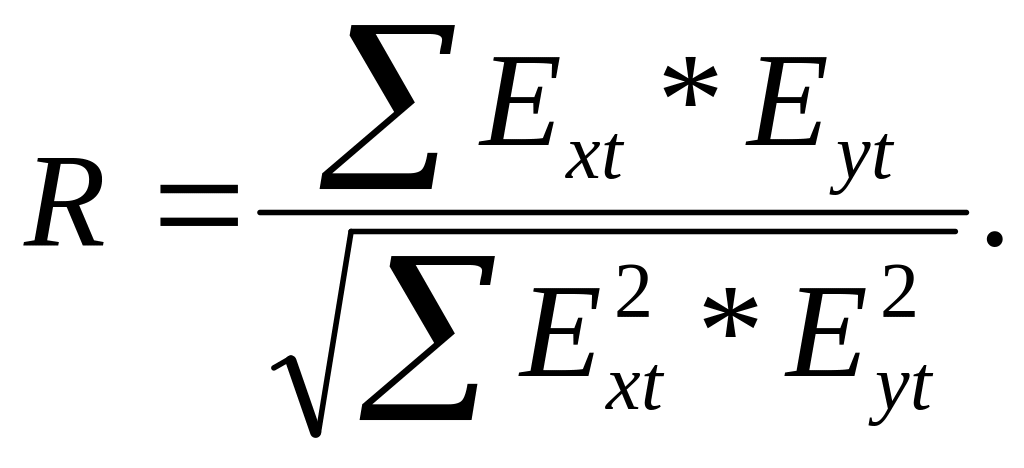2)метод последоват-х разностей – опре-т тесноту связи по первым разностям: 3)ме-д Фишера-Боу – в уравнении регрессии линейно вк-ся фактор времени:Y_t = a₁ +bx_t +c_t . 2) Возможное наличие временного лага т.е. изме-е уровня одногоряда вызывает (измен-е уров-й др.ряда через опред-й иетервал) период в кот-м набл-ся автокорр-я м/у уровнями одного и того же периода, или период отставанияв разв-тии двух взаимосвязанных рядов. Корр-я в двух связ-х рядах динамики возникает если сдвинуть один ряд по отнше-ю другому на период врем-го лага. Для прав-й оцеки тесноты связи вычесляют к-т коррел-ии м/у рядами с различ-й величин-й лага м/у ними: R = 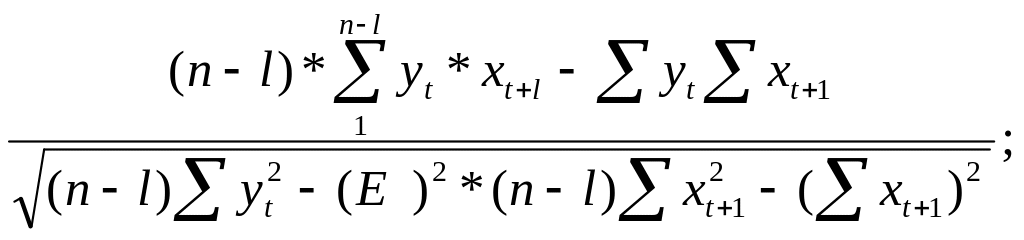Колич-во этих коэ-в не превышает 10. Если в ряду коэ-в есть пик, то значит имется врем-ой лаг.3) Возмож-ь наличия переменной коррел-ии, т.е. показатели связи с течением времени изменяются. Простая корре-я это связь м/у двумя переменными. 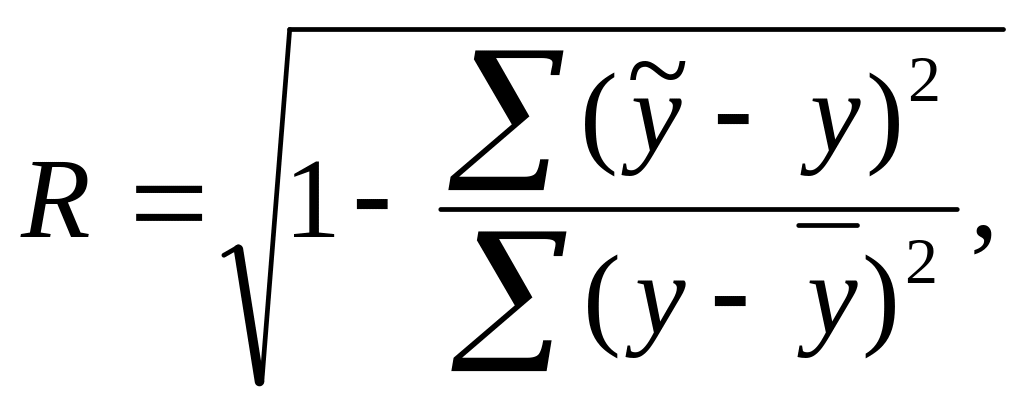Обобщающей оценкой тесноты связи яв-ся индекс корре-и: (0<R<1) пригоден для любой оценки формы связи. Если связь линейная то испо-т линейный к-т корре-ции:

86.Использование адаптивных методов в прогноз-нии.

Метод экспоненциального сглаживания: Его сущ-ть состоит в том что вр. ряд сглаж-ся с помощью временной СС в кот-й веса подчиняются экспоненц-му закону и которая хар-т значение процесса на конце интервала сглаж-ния являясь ср. хар-й послед. уровней ряда.

В процессе выравнивания каждого набл-я исп-ся только значения предыд-х значений уровней ряда динамики взятых с опр-ми весами. Вес каждого набл-я уменьш-ся по мере его удаления от момента для которого опр-ся сглаж. значение: S_t⁽¹⁾ = αy_t+(1- α)S₀^[1], где α - вес или параметр сглаживания(0< α<1); S_t⁽²⁾ = αS_t⁽¹⁾+(1- α)S₀⁽²⁾; S_t⁽³⁾ = αS_t⁽²⁾+(1- α)S₀⁽³⁾. Чем > α тем < сказ-ся влияние предшествующих уравнений и учит-ся влияние лишь послед.наблюдений. Если начальные условия достоверны то необх-мо выбирать небольшое значение α, если нет то большую величину. В прогно-нии, чем длиннее период упреждения тем меньше значение α нужно выбирать. Если есть данные о развитии явления в прошлом то в качестве y₀ можно исп-ть: y₀ = S₀⁽¹⁾ = Σy_t/n.

Если таких данных нет то в качестве y₀ исп-т первое значение ряда динамики y₁. В случке предварительных соображений о выборе нач. условий исп-т:

а)для лин-й модели: y_t = a₀+a₁t. S₀^[1] = a₀ - ((1 - α) /α)a₁;

S₀^[2] = a₀ – (2(1-α)/ α)a₁.

б)Для квадратичной модели: y_t = a₀+a₁t+a₂t²

S₀^[1] = a₀ - ((1 - α) /α)a₁+(((1- α)(2- α))2α²)a₂;

S₀^[2] = a₀ - (2(1 - α) /α)a₁+(((1- α)(3- 2α))α²)a₂;

S₀^[3] = a₀ - (3(1 - α) /α)a₁+((3(1- α)(4- 3α))2α²)a₂;

Оценка коэф-в a^₀, a^₁ a^₂ при построении прогноза

а.) a^₀ = 2S_t^[1] – S_t^[2]; a^₁ = (α/(1- α))( S_t^[1] – S_t^[2]).

Прогноз: y_t+L^* = a^₀+a^₁L.

Ошибка прогноза

где ;

б.) для квадратич. Модели: y_t = a₀+a₁t+0.5a₂t²+Et

a^₀ = 3(S_t^[1] – S_t^[2]+S_t^[3]); a^₁ = α/2(1- α)²[(6-5α)S_t^[1]-2(5-4α)S_t^[2]+(4-3α)S_t^[3]];

a^2 = α²/(1- α)²[S_t^[1] – 2S_t^[2]+S_t^[3]]. Прогноз: y_t+1^* = a^₀+a^₁L+0.5a^2L².

Ошибка прогноза: σ_y+L^* = σ_Et(2α +3α²+3α³L²)^0.5 .

Метод экспон-го сглаж-ния разраб-ный для анализа рядов с большим числом наблюд-й при изуч. экон. рядов (25-30) наблюдений нередко не срабатывает. Проблема выбора начальных условий сводится к оценке погрешности метода. Отсутствует точная методика выбора α.

В настоящее время одним из наиболее перспективных направлений иссл-я вр. рядов явл-ся адаптивные методы кот-е позволяют учесть разл. информ. ценность уровня временного ряда и степени устаревания данных. Оценивание параметров адапт-х моделей осущ-ся на основе рекуррентного метода т.е. эти модели требуют повторения объёма вычислений при появлении новых данных. Достоинством адапт. методов явл-ся построение моделей которые способна учитывать рез-т прогноза, сделанного на предыдущем шаге. Быстроту реакции модели на изменение в динамике процесса хар-т параметр адаптации или параметр сглаживания(дисконтирования).

Адаптивные модели сезонных колебаний.

Если вр. ряды сод-т периодич. сез. колебания то их описывают с помощью след. моделей: 1)y_t = a_1,t*f_t+E_t – модель с мультипликат. коэф. сез-ти; 2)Yt = a_t,1+g_t+E_t – аддитивные коэф-ты сезонности, где a_1,t – хар-ка тенденции развития; f_t – мультипликативные коэф-ты сез-сти; g_t – аддитивные коэф-ты сез-сти.