75.Теория малой выборки
Выборки менее 30 ед-ц наблюдения получили название малых выборок. Рассчёт хар-к ген. сов-ти в данном случае произв-ся на основе среднекв-го отклонения МВ, дисперсии, а так же закона распределения Стьюдента сформулированного последним в 1908 г.
Средне квадр. Откл-я МВ:σмв = σn(n/n-1)0.5;
Процесс вычисления ср.кв. откл-я МВ и ср. ошибки МВ сводится к исправлению, т.е. домножению на поправочные коэфф-ты соотв-х величин, вычисленных по обычным правилам.
Ср. ошибка МВ выч-ся путём испр-я соотв. величины:
Ммв = σn/(n - 1)0.5 ; Предельная ошибка МВ: Δмв = t*Mмв
Распр-е Стьюдента:p(t) = C(1 + (t2/n - 1))-n2/2
Где p(t) – вер-ть события, состоящего в том, что разность м/у выборкой и ген. средней равна – t, С – коэф-т распр-я Стьюдента.
Кривая распр-я Ст-та отл-ся от кривой норм-го распр-я, хотя и при n → ∞ соотв-тей.
76.Типическая выборка
Даёт более точные рез-ты, чем остальные. Разбивается на группы, причём возможны 2 основных способа формирования типичной выборки: а.) отбор, непропорциональный объёму типич. групп;
Здесь для типич. n группы отбираются по одинаковому кол-ву:
ni = n/k; где ni – кол-во отбираемых из i – й типичной группы элементов., k – кол-во типичных групп.
б.) отбор, пропорц-й объёму типич. групп, при кот-м из каждой тип. группы отбир-ся число элементов, пропорц-е её объёму:
ni = n*(N/Ni) , где n – общий объём выборки; N – общий объём ген. сов-ти; Ni – объём типичной группы;
Также различают повторный и безповторный
типич. отборы.
Повторный отбор непропорциональный
для средней
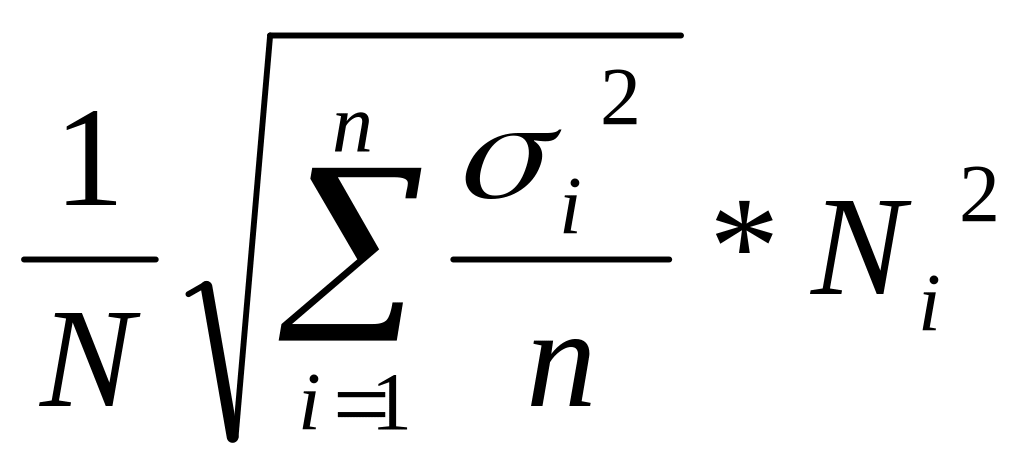
для доли
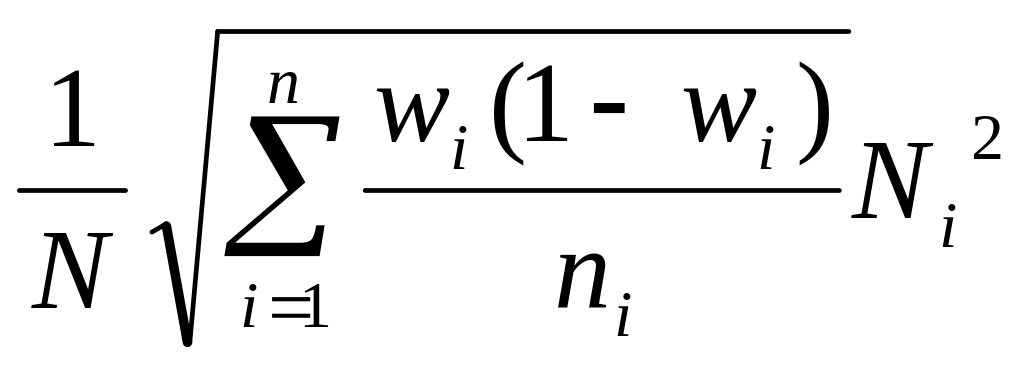
Пропорциональный для средней (σiср2/n)0.5 , для доли ((w(1-w))/n)0.5
((w(1-w)) –
ср. арифм. величина из дисперсий
альтернативного признака выборок из
i – х типич. групп, σiср2
– ср. арифм. из дисперсий, σi2
– дисперсия выборки из i
– й типич. группы. Бесповторный отбор
непропорциональный для средней
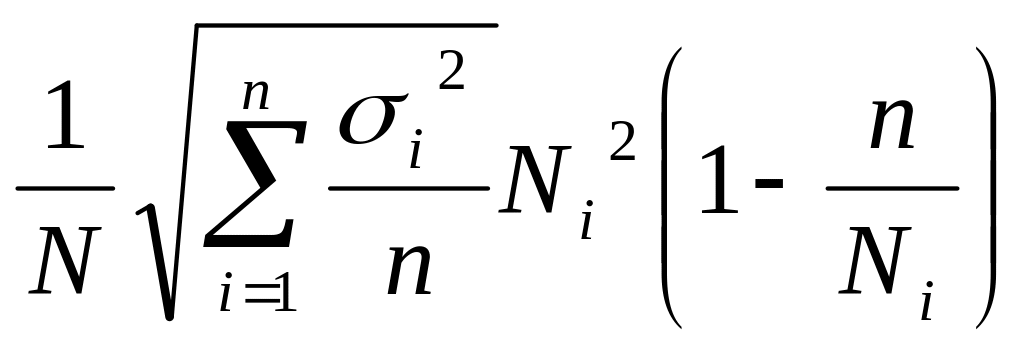
для доли
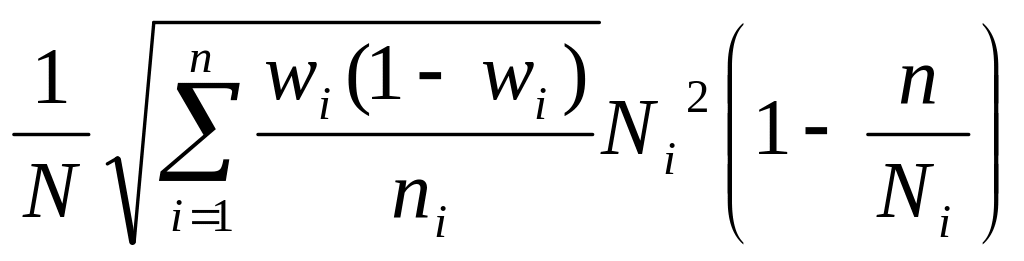
Пропорциональный для средней ((σiср2/n)(1-n/ni))0.5
для доли (((w(1-w))/n)(1-n/Ni))0.5
77.Серийная выборка
Применяется тогда, когда собственно случ. отбор, механич. отбор, типич. отбор либо невозможны, либо нецелесообразны. В качестве иссл-го признака при серийной выборке будет выступать либо ср. вел-на иссл-го признака, либо доля единиц, обладающих альтерн-м признаком отобранной серии, а в качестве ед-ц набл-я отобранные серии. В связи с этим ф-лы ср. ошибки и численности выборки в принципе идентичны соотв-м выражениям при собственно случ. отборе.
Повт. отбор (δсрx2/ν)0,5 (δсрp2/ν)0,5
Бесповт. отбор ((δсрx2/ν)(1-r/R))0,5 ((δсрp2/ν)(1-r/R))0,5
Где R – число серий в ген. сов-ти (N), ν – число отобранных серий (r), δсрx2 – межсерийная дисперсия средних величин, δсрp2 – межсерийная дисперсия доли единиц, обладающих ислл-м признаком(альт-м)
78.Комб-ная выборка. Расчет ср-й ошибки комб-ной выб-ки.
В тех случаях когда ген. сов-ть дост-но велика и изначально разбита на равновеликие и многочисленные серии целесообразно применять комбинированный отбор. Он предполагает случ. отбор серий, из кот-х потом также на основе жеребьёвки произ-ся отбор отд-х ед-ц наблюдения. Данный вид отбора сочетает в себе серийный отбор с собственно-случайным. В связи с этим формулы ср.ошибки комбинированной выборки вкл-т в себя слагаемые напоминающие соответствующие элементы формул ср. ошибки собственно-случайной и серийной выборок.
Особенности комбинированной выборки закл-ся в том, что после отбора на основе обсл-я входящих в их состав единиц наблюдения опр-ся дисперсии изуч-го признака внутри отобранных серий – серийные дисперсии. Затем для ряда серийных дисперсий выч-ся ср. дисперсия, а на основе этих результатов расч-ся межсерийная дисперсия (дисперсия серийных дисперсий).
Повторный отбор Бесповторный отбор
Для ср-ей (σiср2/n+ σx2/r)0.5 ((σi2/n)*(1-n/nr) + (σx2/r)*(1-r/R))0.5
Для доли (w(1-w)ср/n+σp2/r)0.5 ((w(1-w)ср/n)*(1-n/nr)+(σp2/r)*(1-r/R))0.5
Где σiср2 - средняя дисперсия из серийных дисперсий количественного признака, σx2 - межсерийная дисперсия колич-го признака, w(1-w)ср средняя дисперсия из серийных дисперсий альтернативного признака w(1-w)ср = (Σ( wi(1-wi)*ni))/n, σp2 – межсерийная дисперсия альтернативного признака, nr – число ед-ц наблюдения отобранных из генеральной сов-ти в составе серий, n – число единиц наблюдения составивших выборку, r – число отобранных серий, R – число серий в генер-й сов-ти.