2.5. Контрольные вопросы

1. Перечислить основные разновидности трений в природе.

2. Пояснить закономерности, возникающие при движении тела в жидкости или газе.

3. Какова физическая сущность трения?

4. Какая сила должна быть приложена к телу, расположенному на горизонтальной плоскости, чтобы сдвинуть его на этой плоскости?

5. К стальному ящику массой 500 кг, стоящему на бетонном полу, приложена в горизонтальном направлении постоянная сила, равная 1600 Н. Будет ли под действием такой силы ящик двигаться? Если да, то как он будет двигаться: равномерно или ускорено.

Лабораторная работа №3

Определение логарифмического декремента затухания, коэффициента затухания и коэффициента сопротивления

Цель работы – экспериментально определить логарифмический декремент затухания, коэффициент затухания и коэффициент сопротивления.

Оборудование – система обработки данных 3B NETlog^TM, датчик ускорения (+5g), колебательная система, соединительный кабель с 8-контактными разъемами типа miniDIN, компьютер.

3.1. Теоретическое обоснование работы

Колебательным движением называется такое движение, при котором тело, выйдя из некоторого начального положения, многократно возвращается к нему.

Всегда, когда выводят тело из положения устойчивого равновесия, возникает сила, стремящаяся возвратить тело в положение равновесия. Но наличие только такой возвращающей силы недостаточно для возникновения колебательного движения. Должна существовать другая сила, которая непозволила бы телу остановиться в положении равновесия. Этой силой в большинстве технически важных случаях является инерция колеблющегося тела.

Среди разнообразных колебаний, встречающихся в природе и технике, особую роль играют гармонические колебания. Гармоническим колебательным движением называется такое колебательное движение, при котором ускорение а прямо пропорционально смещению S от положения равновесия и направлено к положению равновесия, т.е.:

_{. (3.1)}

_{Возвращающая сила при этом также пропорциональна смещению колеблющегося тела и направлена к положению равновесия:}

_(3.2)

_{Математически гармоническое колебательное движение описывается уравнением:}

где S – отклонение колеблющейся величины от положения равновесия;

А – амплитуда колебания, т.е. максимальное отклонение колеблющейся величины от положения равновесия;

ω – циклическая частота;

t – время от начала отсчета колебания;

φ – начальная фаза колебания, характеризует положение колеблющейся величины в начальный момент времени t=0.

Скорость колеблющейся величины находится как первая производная от отклонения по времени:

_(3.3)

Ускорение колеблющейся величины находится как первая производная скорости по времени или вторая производная от отклонения по времени, т.е.:

_(3.4)

По второму закону Ньютона произведение массы тела на ускорение равняется действующей силе F=ma. При гармоническом колебательном движении возвращающая сила пропорциональна смещению (формула (3.2)). Здесь коэффициент k называют коэффициентом упругости. Подставляя в формулу второго закона Ньютона вместо F и a их значения, определяемые формулой (3.1) и (3.2), получим:

ma=-mω²S=-kS, (3.5)

откуда

k=mω². (3.6)

Во всех реальных колебательных системах процесс колебания связан с преодолением различных препятствий. Независимо от их природы будем называть эти силы сопротивления силами трения. Наибольшее значение в технике имеют такие силы трения, которые пропорциональны скорости движения

(3.7)

где r – коэффициент пропорциональности, называемый коэффициентом сопротивления. Знак минус указывает на то, что сила препятствует движению. При отсутствии сил трения энергия колеблющейся системы сохраняется. Такие системы называют консервативными. При наличии сил трения энергия будет уменьшаться со временем, рассеиваться в окружающей среде. Такие системы называют диссипативными. Так как энергия пропорциональна квадрату амплитуды, то уменьшение энергии ведет к уменьшению амплитуды. Колебания будут затухающими. На рис. 3.1 показан график затухающего колебания.

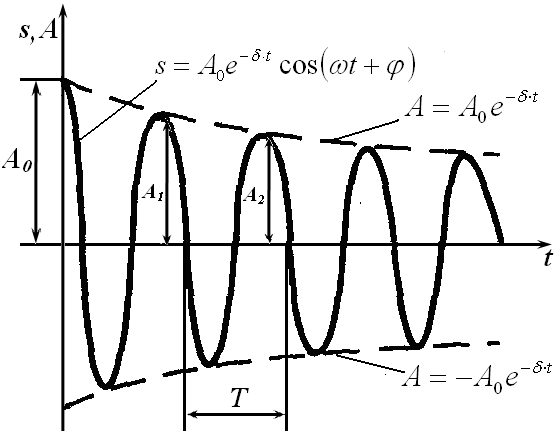
Рисунок 3.1 – График затухающего колебания

При наличии сил трения в формулу (3.5) войдет дополнительный член, определяемый формулой (3.7) и уравнение примет вид:

_.

Или

. (3.8)

Заменим а и υ по формулам (3.4) и (3.3) и уравнение (3.8) примет вид:

. (3.9)

В последнем уравнении заменим k по формуле (3.6), тогда

, (3.10)

. (3.11)

Положим, что

. (3.12)

Величину β называют коэффициентом затухания. В этих обозначениях:

.

Решение этого дифференцированного уравнения примет вид:

, (3.13)

где ω – циклическая частота, ;

А₀ - амплитуда при t = 0;

– амплитуда в момент времени t;

ω₀ – циклическая частота колеблющейся системы при отсутствии сил трения, т.е. при β = 0.

Из равенства (3.13) следует, что колебание будет синусоидальным, но амплитуда будет уменьшаться со временем по экспоненте.

Колебательное движение будет возможно при условии ω₀ > β. При , тело, отклоненное от положения равновесия, возвращается к нему без колебаний.

Определим отношение амплитуд А₁ и А₂ затухающих колебаний в моменты времени, отличающиеся на один период, т.е. при t и t+T:

. (3.14)

Возьмем натуральный логарифм от обоих частей равенства (3.14):

Тогда

. (3.15)

Логарифм отношения двух соседних амплитуд затухающего колебания называется логарифмическим декрементом затухания:

(3.16)