Лекция 15

Краткое содержание: Дифференциальные уравнения движения механической системы Теорема об изменении количества движения механической системы в дифференциальной и конечной формах. Теорема о движении центра масс механической системы. Теорема об изменении об кинетического момента механической системы. Теорема об изменении кинетической энергии механической системы . Работа системы сил. Сумма работ внутренних сил в твердом теле. Закон сохранения механической энергии. Теорема Кёнига. Кинетическая энергия абсолютно твердого тела в частных случаях движения

Дифференциальные уравнения движения СМТ

На основании второго (основного) закона динамики в форме для каждой МТ можно записать:

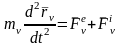(=1, 2, ..., n). (1)

Система (1) является системой n дифференциальных уравнений движения СМТ в векторной форме.

Если спроектировать соотношения (1) на оси декартовой системы координат, то получим систему 3n дифференциальных уравнений движения СМТ в координатной форме:

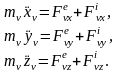=1, 2, ..., n (2)

Теорема об изменении количества движения СМТ

Второй основной закон динамики для -й МТ, входящей в СМТ, с учетом классификации сил, действующих на нее, можно записать в форме:

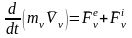(=1, 2, ..., n). (1)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

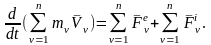(2)

Используем формулу для главного вектора сил и учтем свойство внутренних сил:

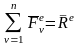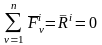, , (3)

где 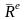– главный вектор всех внешних сил, – главный вектор всех внутренних сил.

Количеством движения СМТ называется геометрическая сумма количеств движений МТ, входящих в СМТ:

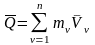. (4)

Подставляя выражение (3) и (4) в соотношение (2), получим теорему об изменении количества движения СМТ в дифференциальной форме:

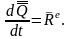(5)

Теорема: Производная по времени от количества движения СМТ равна главному вектору внешних сил, действующих на СМТ.

Проектируя соотношение (5) на оси декартовой системы координат, получим:

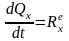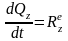, , . (6)

Из формулы (6) следует, что производная по времени от проекции количества движения СМТ на какую-либо ось декартовой системы координат равна сумме проекций на эту же ось приложенных к СМТ внешних сил.

Умножим обе части соотношения (5) на dt:

.

Проинтегрировав это выражение, считая, что в начальный момент времени количество движения СМТ было равно 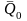, получим теорему об изменении количества движения СМТ в конечной форме:

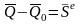. (7)

Здесь 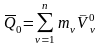, 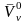– скорость движения -й МТ в начальный момент времени, а 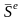– импульс главного вектора внешних сил или сумма импульсов внешних сил, действующих на СМТ за промежуток времени t:

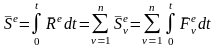. (8)

Теорема: Изменение количества движения СМТ за конечный промежуток времени равно сумме импульсов всех внешних сил, действующих на СМТ, за тот же промежуток времени.

В проекциях на оси декартовой системы координат эта теорема в конечной форме имеет вид:

,

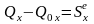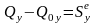, (9)

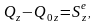
т.е изменение проекции количества движения СМТ за конечный промежуток времени равно сумме проекций импульсов всех внешних сил, действующих на СМТ, за тот же промежуток времени.

Следствия:

• Если 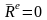, то из соотношения (5) следует, что .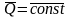

Если главный вектор внешних сил, действующих на СМТ, равен нулю, то количество движения СМТ постоянно по величине и направлению и равняется количеству движения СМТ в начальный момент времени: 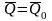. (10)

Если 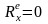, то из первого соотношения (6) следует, что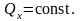

Соотношение (10) представляет собой закон сохранения количества движения СМТ.

Теорема о движении центра масс СМТ

Считая, что массы МТ постоянны, преобразуем формулу, определяющую количество движения СМТ, следующим образом:

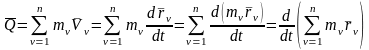. (1)

На основании определения центра масс 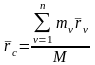, поэтому:

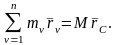(2)

Подставляя соотношение (2) в (1), получим: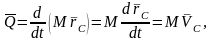

Таким образом, количество движения СМТ равно количеству движения, которое имел бы центр масс СМТ, если бы в нем была сосредоточена вся масса СМТ

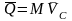. (3)

Подставляя (3) в теорему об изменении количества движения СМТ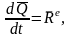

получим теорему о движении центра масс СМТ в векторной форме:

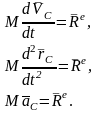(4)

Теорема: Центр масс СМТ движется как МТ, в которой сосредоточена вся масса СМТ и к которой приложены все внешние силы, действующие на СМТ.

Проектируя второе соотношение формул (4) на оси декартовой системы координат, получим дифференциальные уравнения движения центра масс СМТ в проекциях на оси декартовой системы координат:

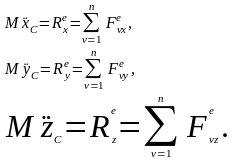(5)

Из теоремы о движении центра масс СМТ можно получить два следствия, аналогичные закону сохранения количества движения СМТ.

Следствия:

• Если , то из первого соотношения формул (4) следует .

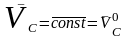Если главный вектор внешних сил, действующих на СМТ, равен нулю, то СМТ движется так, что скорость центра масс СМТ постоянна по величине и направлению и равна скорости центра масс в начальный момент времени.

Если , то из первого соотношения уравнений (5) следует, что .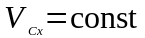

Если проекция главного вектора внешних сил СМТ на какую-либо ось равна нулю, то СМТ движется так, что проекция скорости центра масс СМТ на эту ось является постоянной величиной и равна проекции скорости центра масс на эту ось в начальный момент времени.

Теорема об изменении кинетического момента смт

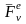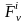Запишем теорему об изменении момента количества движения МТ для -й точки СМТ, учтя, что на нее действуют – равнодействующая всех внешних сил и – равнодействующая всех внутренних сил:

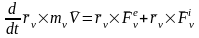. (=1,2,...,n)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

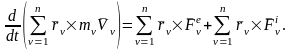(1)

Используя формулу для главного момента системы сил и учтя свойство внутренних сил, имеем:

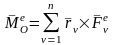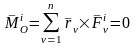, , (2)

где 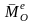- главный момент всех внешних сил, а 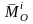- главный момент всех внутренних сил относительно какого-либо центра.

Введем понятие кинетического момента СМТ относительно какого-либо центра О.

Определение: Кинетическим моментом или моментом количества движения СМТ называется геометрическая сумма моментов количества движения МТ, входящих в СМТ, относительно того же центра:

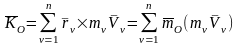. (3)

Подставив (2) и (3) в (1), получим теорему об изменении кинетического момента СМТ в следующем виде:

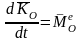. (4)

Теорема: Производная по времени от кинетического момента СМТ относительно какого-либо центра равна главному моменту всех внешних сил, действующих на СМТ, относительно того же центра.

Спроектировав соотношения (4) на оси декартовой системы координат с началом в центре О и учтя связь между моментами силы относительно точки и оси, получим:

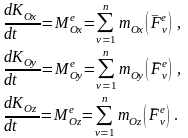(5)

Отсюда следует, что производная по времени от проекции кинетического момента СМТ на какую-либо ось равна проекции главного момента всех внешних сил, действующих на СМТ, на эту ось или сумме моментов всех внешних сил, действующих на СМТ, относительно этой оси.

Следствия:

• Если 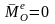, то из соотношения (4) следует, что .

• Если главный момент внешних сил, действующих на СМТ, относительно какого-либо центра равен нулю, то кинетический момент СМТ относительно того же центра постоянен по величине и направлению и равен кинетическому моменту СМТ относительно того же центра в начальный момент времени:

Если 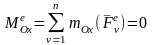, то из первого соотношения (4.25) следует .

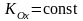Если проекция главного момента всех внешних сил, действующих на СМТ, на какую-либо ось (сумма моментов всех внешних сил относительно какой-либо оси) равна нулю, то проекция кинетического момента на эту ось является постоянной величиной и равняется проекции кинетического момента на эту ось в начальный момент времени

Теорема об изменении кинетической энергии смт

Используя теорему об изменении кинетической энергии МТ для -й точки СМТ запишем:

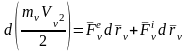(=1,…,n),

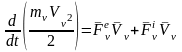(=1,…,n),

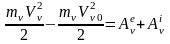(=1,…,n).

Просуммировав эти соотношения и учитывая, что производная от суммы равна сумме производных, получим:

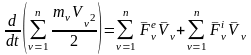, (1)

.

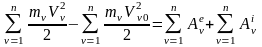Введем понятие кинетической энергии СМТ.

Определение: Кинетической энергией СМТ называется величина, равная сумме кинетических энергий входящих в нее МТ:

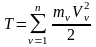, (2)

аналогично 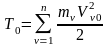. (3)

Здесь Т и Т₀ – соответственно значения кинетической энергии СМТ в текущий и начальный моменты времени.

По определению в соотношениях (1):

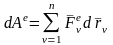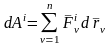, –суммы элементарных работ всех внешних и внутренних сил, действующих на СМТ;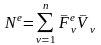 , 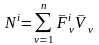–соответственно суммы их мощностей;

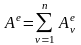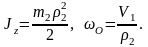, –соответственно суммы работ всех внешних и внутренних сил, действующих на СМТ.

С учетом принятых обозначений, из соотношений (1) получим три формы (две дифференциальных и одну конечную) теоремы об изменении кинетической энергии СМТ.

Теорема: Дифференциал кинетической энергии СМТ равен сумме элементарных работ всех внешних и внутренних сил, действующих на СМТ.

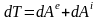. (4)

Теорема: Производная от кинетической энергии СМТ равна сумме мощностей всех внешних и внутренних сил, действующих на СМТ.

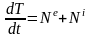. (5)

Теорема: Изменение кинетической энергии СМТ на ее конечном перемещении из одного положения в другое равно сумме работ приложенных внешних и внутренних сил, на том же перемещении.

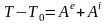. (6)

Рассмотрим сумму элементарных работ всех внутренних сил, действующих на СМТ.

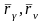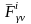Выделим из СМТ две произвольные МТ В_ и B_, положение которых относительно неподвижного центра О определяется радиус-векторами . Обозначим через и 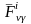( 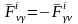) силы взаимодействия между этими МТ и определим сумму элементарных работ этих сил (рис):

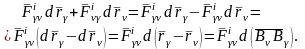
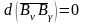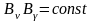Из полученного соотношения следует, что элементарная работа внутренних сил, с которыми две точки СМТ действуют друг на друга, будет равна нулю только в случае , т. е. когда , что имеет место в случае НМС.

Таким образом, сумма элементарных работ всех внутренних сил НМС всегда равна нулю. Аналогичным образом можно доказать, что суммы мощностей всех внутренних сил НМС и их работ будут равны нулю. Учитывая это, на основании соотношений (4) – (6) для НМС можно записать: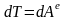 , , .
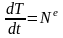
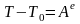