2) Метод группировки данных

Группировка – это разделение совокупности данных на группы с целью изучения ее структуры или взаимосвязей между компонентами. В процессе группировки единицы совокупности распределяются по группам в соответствии со следующим принципом: различие между единицами, отнесенными к одной группе, должно быть меньше, чем различие между единицами, отнесенными к разным группам.

Важный вопрос при проведении анализа с помощью метода группировки – выбор интервала группировки. Существуют два основных подхода к его решению:

- первый подход (чаще используемый) предполагает деление совокупности данных на группы с равными интервалами значений. Формула Стерджесcа:

x_max, x_min – максимальное и минимальное значение признака в изучаемой совокупности соответственно;

k – число групп;

N – число наблюдений.

Очевидно, что знаменатель дроби = количеству групп или интервалов, на которое разбивается исходная совокупность. Таким образом, оптимальное количество групп, соответствующее некоторому числу наблюдений, согласно формуле Стерджесcа:

Число наблюдений (N)	15-24	25-44	45-89
Число групп (k)	5	6	7

- второй подход – интервалы группировки можно выбрать неравными (возрастающими или убывающими). Этот подход обычно применяется при большой вариации и неравномерности распределения признака по всему интервалу его изменения. При выборе размера интервала руководствуются здравым смыслом и логикой. При использовании этого подхода интервалы часто выбирают таким образом, чтобы группы были равнозаполненными.

Существенную помощь в анализе групп совокупности оказывает графическое изображение.

Группы рабочих по производительности, шт/смену xj	Количество рабочих fj	Накопленная частота fj'	Середина интервала, шт/чел xj'
10-15 15-20 20-25 25-30 30-35 35-40 40-45 45-50 50-55	6 9 20 41 26 21 14 5 1	6 15 35 76 102 123 137 142 143	12,5 17,5 22,5 27,5 32,5 37,5 42,5 75,2 52,5
Итого	143

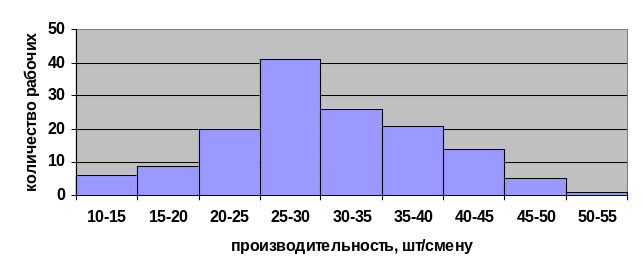
Рис. Графическое изображение групп

3) Элементарные методы обработки расчетных данных

При изучении совокупности значений изучаемых величин, помимо средних, используют и другие характеристики. При анализе больших массивов данных обычно интересуются двумя аспектами:

1. величинами, которые характеризуют ряд значений как целого (средние величины, середина интервала, мода и медиана);

2. величинами, которые описывают различия между членами совокупности, т.е. характеристиками разброса (вариации) значений.

Середина интервала:

Мода – такое значение изучаемого признака, которое среди всех его значений встречается наиболее часто. Если все значения встречаются по одному разу или равное количество раз, такая совокупность является безмодальной.

x₀ – нижняя граница модального интервала;

f_Mo – частота в модальном интервале;

f_Mo-1 – частота в предыдущем интервале;

f_Mo+1 – частота в следующем интервале за модальным;

i – величина интервала.

∆ расчета медианы по таблице

Медиана – такое значение изучаемой величины, которое делит изучаемую совокупность на две равные части, в которых количество членов со значениями меньше медианы равно количеству членов, которые больше медианы. Медиану можно найти только в совокупностях данных, содержащих нечетное количество значений.

В отличие от средней, медиана не зависит от крайних значений показателей. Например, если максимальное значение изучаемого показателя увеличится, то все средние возрастут вместе с ним. Медиана останется неизменной.

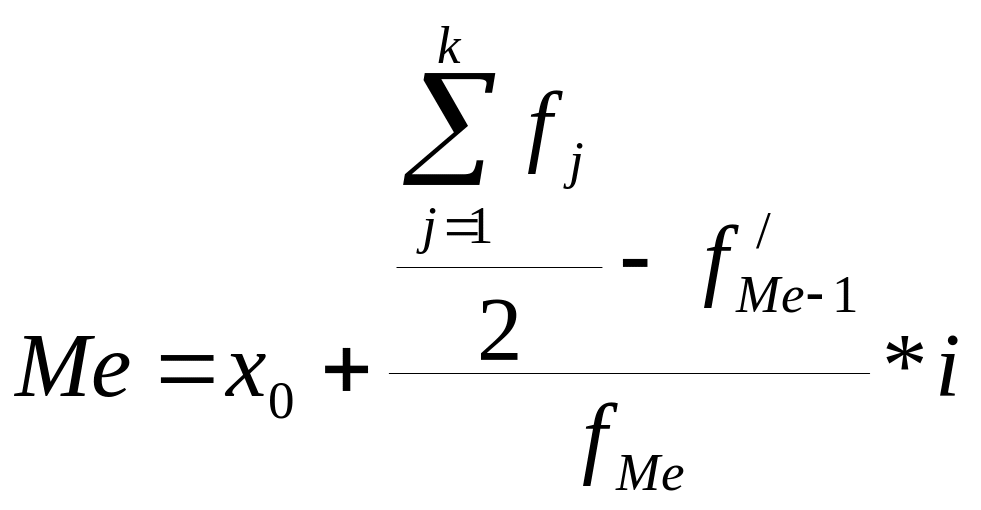
х₀ – нижняя граница интервала, в котором находится медиана;

f^`′_Me-1 – накопленная частота в интервале, предшествующем медианному;

f_Me – частота в медианном интервале.

Размах вариации:

R=Xmax-Xmin - характеризует разброс величины.

Var коэффициент вариации

Критическое значение 33%. Если Var >33%, то совокупность нельзя назвать однородной.

Коэффициент асимметрии → 0 , значит распределение величин симметрично:

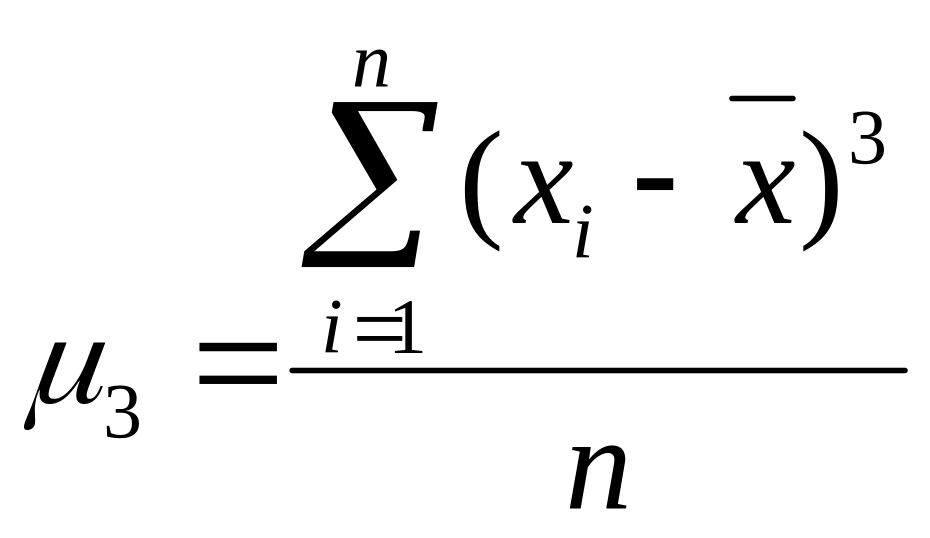
Эксцесс:

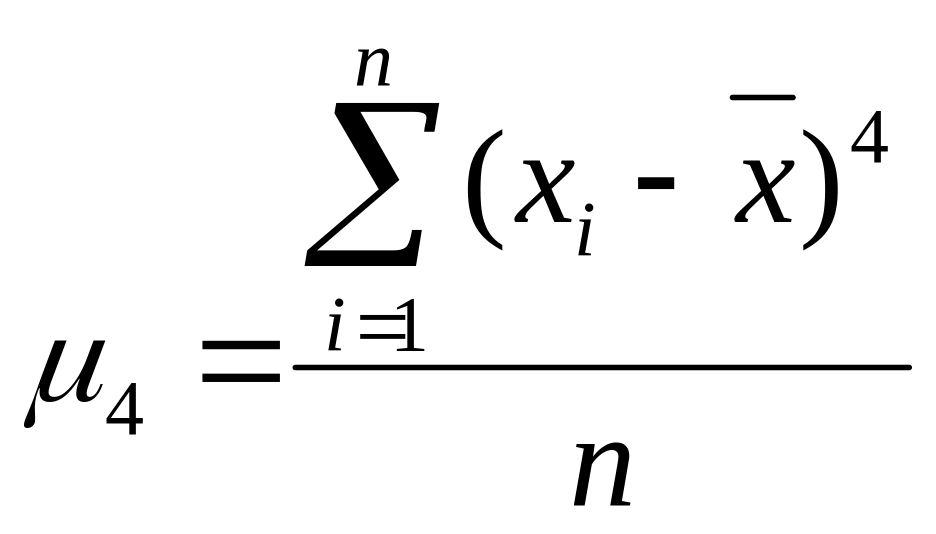
Ex→0 означает нормальное распределение.

Большой положительный эксцесс означает, что в совокупности данных есть слабо варьирующее по данному признаку «ядро», окруженное редкими, сильно отстоящими от него значениями. Большое отрицательное значение показателя эксцесса говорит об отсутствии такого «ядра».