Министерство образования Российской Федерации

Новосибирский государственный техниЧеский университет

ПРАКТИЧЕСКИЙ КУРС

ТЕОРЕТИЧЕСКИХ

ОСНОВ

ЭЛЕКТРОТЕХНИКИ

Сборник задач для студентов очной

и дистанционной форм обучения

Часть II

Новосибирск

2003

Коллектив авторов:

Б.В. Литвинов, В.Т. Мандрусова, Ю.В. Петренко, Н.А. Юрьева

Рецензент

канд. техн. наук, зав. кафедрой «Общая электротехника»,

доц. В.В. Богданов

Работа выполнена на кафедре

«Теоретические основы электротехники»

© Новосибирский государственный

технический университет, 2003

I . Классический метод расчета переходных процессов в линейных электрических цепях с сосредоточенными параметрами Основные вопросы

1. Законы коммутации.

2. Представление переходной величины в виде суммы принужденной и свободной составляющих.

3. Определение принужденной составляющей.

4. Определение свободной составляющей.

5. Способы составления характеристического уравнения:

а) по дифференциальному уравнению определяемой величины;

б) с помощью алгебраизации системы интегрально-диффе­ренциальных уравнений;

в) с помощью выражения входного сопротивления Z(p).

6. Виды корней и их связь с характером переходного процесса.

7. Определение независимых и зависимых начальных условий.

ЛИТЕРАТУРА

1. Зевеке Г.В., Ионкин П.А., Нетушил Л.В., Страхов С.В. Основы теории цепей. – М.: Энергия, 1975.

2. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. – М.: Энергия, 1966. – Т. 2. – Гл. 10.

3. Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1978. – § 283–310.

ПРИМЕРЫ

Задача 1

В схеме (рис. а) R₁ = R₂ = 10 Ом; L = 0,2 Гн; Е = 80 В. Ключ К₂ замыкается через 12 мс после замыкания ключа К₁ .

Определить переходный ток i(t).

Р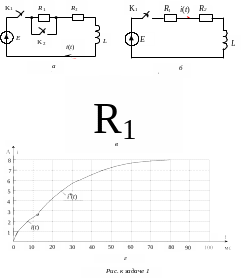 ешение

Так как в цепи поочередно замыкаются два ключа, возникает два переходных процесса, следующих один за другим. Поэтому задача имеет два самостоятельных решения (для временных интервалов 0  t  12 мс и 12 мс  t  ). Расчет переходного процесса основан на решении дифференциального уравнения, описывающего режим цепи после коммутации.

Переходный процесс после замыкания ключа К₁ (рис. б) (0  t  12 мс))

• Д ифференциальное уравнение, характеризующее режим в цепи после коммутации (на основании второго закона Кирхгофа):

(1)

. (1)

• Общее решение уравнения (1):

. (2)

• Принужденная составляющая тока:

. (3)

• Характеристическое уравнение дифференциального уравнения (1):

, (4)

откуда с^–1,

тогда свободная составляющая искомого тока

i_св(t) = Ae^–100t . (5)

• С учетом (2) переходный ток в рассматриваемом временном диапазоне определится соотношением:

i(t) = 4 + Ae^–100t. (6)

• Расчет постоянной интегрирования А. В начальный момент переходного режима (t = 0) выражение (6) принимает вид

. (7)

По первому закону коммутации (ток в индуктивности ни при каких условиях не изменяется скачком)

i_L(0₊) = i_L(0_). (8)

До коммутации i_L(0_) = i(0_) = 0, следовательно, i(0₊) = 0. Тогда соотношение (7) примет вид 0 = 4 + A, откуда А =  4 .

• Окончательно, для интервала 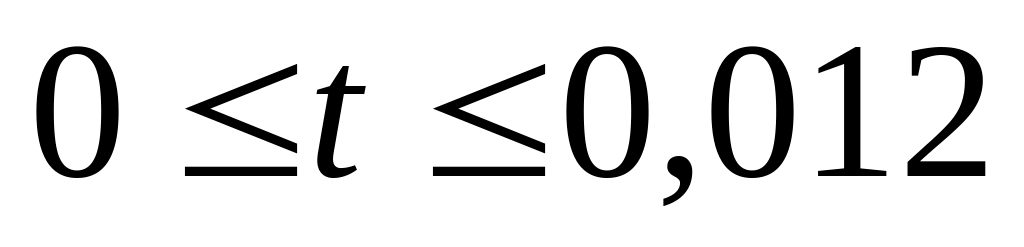с

А. (9)

2. Переходный процесс после замыкания ключа К₂ (рис. в) (0,012 с  t  ).