
- •!!!!!!!!Etapy podejmowania decyzji!!!!!!!!!
- •Zasada niedostatecznej racji.
- •Ilość stanów świata (jeżeli są 3 to 3)
- •Problem (loteria)
- •Model williamsona użyteczności menedżerskiej
- •Im większe są składniki s, m, d, tym większe jest zadowolenie menedżera.
- •Model marrisa wzrostu firmy menedżerskiej
- •Wykres – funkcja zysku I próg rentowności
- •Duopol: zyski firm I optymalna reakcja
Wykres – funkcja zysku I próg rentowności
Dla q >0,
![]()
![]() ,
gdy
,
gdy
![]() -
strata
-
strata
![]() ,
gdy
,
gdy
![]() -
zysk
-
zysk
![]() ,
gdy
,
gdy
![]() -
próg rentowności
-
próg rentowności
NEOKLASYCZNA TEORIA FIRMY
Cel: Produkcja na poziomie
![]() ,
dla którego zysk
,
dla którego zysk
![]() jest najwyższy (maksimum zysku).
jest najwyższy (maksimum zysku).
![]() -
optymalny poziom produkcji
-
optymalny poziom produkcji
Firma produkując q jednostek jest w stanie równowagi.
Kiedy funkcja ma maksimum?
Warunek konieczny I rzędu:
![]() ,
czyli
,
czyli
![]()
tzn. ![]()
in. przychód krańcowy = koszt krańcowy
Słowami:
Jeśli jest maksymalizującym zysk poziomem produkcji, to przychód uzyskany ze sprzedaży dodatkowej jednostki jest równy kosztowi jej wytworzenia.
![]() ,
a więc
,
a więc
![]() .
.
Warunek
maksymalizacji zysku
![]() zachodzi
zachodzi
![]()
![]() .
.
Niech p będzie ceną towaru (wartość jednostki towaru.
![]() ←
wskaźnik Lernera [Abba Lerner, 1934]
←
wskaźnik Lernera [Abba Lerner, 1934]
L – procentowy narzut na koszt krańcowy, margines zysku (ang. markup, profit margin),
marża (fr. marge)
Maksymalizacja zysku: uzupełnienie
Maksymalizacja zysku jest szukaniem wartości największej zysku, a więc maksimum globalnego funkcji zysku dla
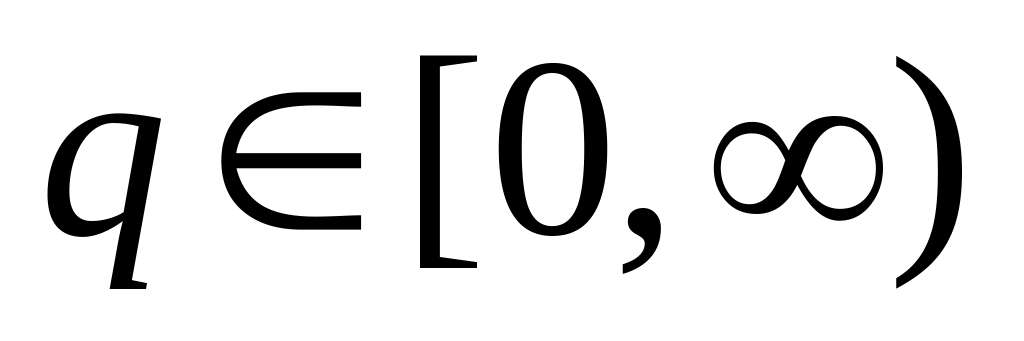 .
.Warunek konieczny określa tylko te
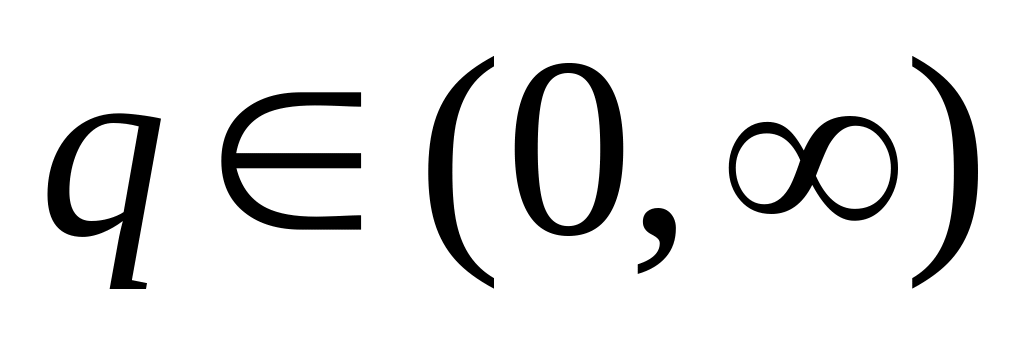 ,
które mogą być maksimum lokalnym funkcji zysku. Może się
okazać, że funkcja zysku ma maksimum globalne dla q = 0
(nieopłacalna produkcja).
,
które mogą być maksimum lokalnym funkcji zysku. Może się
okazać, że funkcja zysku ma maksimum globalne dla q = 0
(nieopłacalna produkcja).Bardziej realistyczny wariant zadania maksymalizacji zysku zawęża rozpatrywane poziomy produkcji do
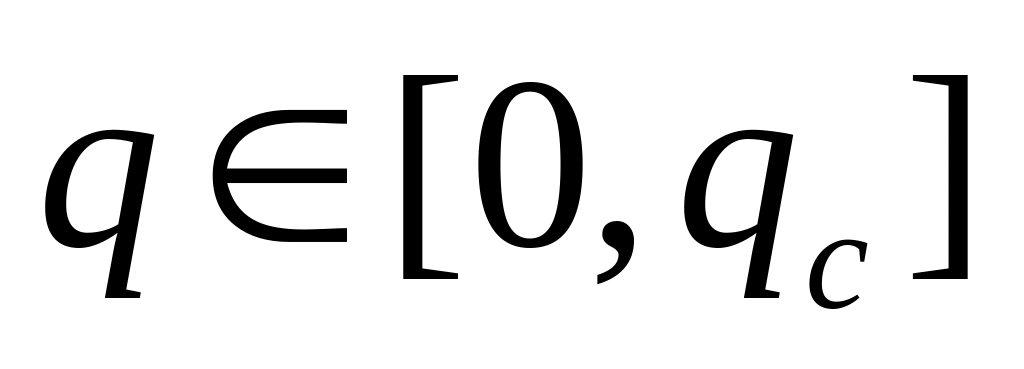 ,
gdzie (skończone) qc określone jest przez dostępne
moce wytwórcze.
,
gdzie (skończone) qc określone jest przez dostępne
moce wytwórcze.Spełnienie dla jakiegoś warunku koniecznego nie gwarantuje, że takie q określa maksimum lokalne funkcji zysku . Jednak, jeśli stopa zmian przychodu krańcowego MR jest niższa od stopy zmian kosztu krańcowego MC, to dla takiego poziomu produkcji q funkcja zysku ma maksimum lokalne.
Koszt przeciętny AC(q), a koszt krańcowy MC(q)
; .
Krańcowy
koszt przeciętny:
![]() !
!
![]()
Koszt przeciętny AC rośnie, gdy MC > AC;
koszt przeciętny maleje, gdy MC = AC.
!!! Stąd wynika:
Koszt przeciętny jest najmniejszy, gdy MC = AC.
Dla innych wielkości, np. przychodu R, analogicznie.
Funkcja kosztu
Koszt krańcowy MC(q) = C`(q). Na początku, gdy produkcja rośnie, koszt krańcowy maleje, potem rośnie. Koszt przeciętny pokrywa się z kosztem krańcowym – mierzony styczną do wykresu funkcji kosztu ma takie samo odchylenie jak sieczna do tej funkcji.
Funkcja kosztu:
ma wartości dodatnie,
im więcej produkujemy, tym większy koszt.
Krzywa kosztu przeciętnego jest U-kształtna.
MES (minimal efficient scale – minimalna skala efektywna) – punkt, w którym koszt przeciętny jest najmniejszy – czyli koszt wyprodukowania jednostki jest najmniejszy(?).
Koszt przeciętny AC w zależności od przemysłu
Istnieje duży zakres produkcji, w którym nieznacznie zmienia się koszt wyprodukowania jednostki towaru.
MES – ten poziom produkcji, który określa taką cenę równą AC, aby firma produkowała bez
strat!
Przykładowa funkcja kosztu C(q) firmy
Por. [A.C. Chiang, 1994, str. 255-257)]
Wymagania: ![]() oraz
oraz
![]() zawsze;
zawsze;
dla
![]() ,
,
![]() maleje;
maleje;
dla
![]() - rośnie.
- rośnie.
Stąd:
dla
![]() koszt krańcowy MC jest minimalny.
koszt krańcowy MC jest minimalny.
Najprostszą
funkcją spełniającą wymagania jest wielomian trzeciego stopnia
![]() ,
gdy
,
gdy
![]() oraz
oraz
![]() .
.
Koszt
krańcowy jest najmniejszy, gdy
![]() .
.
POPYT RYNKOWY
Funkcja popytu „rynkowego” to przyporządkowanie D: „cena p” „całkowita ilość Q rozpatrywanego towaru, którą konsumenci przy cenie p zakupią”.
Prawo popytu: wzrost ceny zmniejsza sprzedaż.
Funkcja popytu
F. popytu (prawo popytu) ma zastosowanie przede wszystkim do towarów o charakterze masowym (powinna być odniesiona do rynku masowego).
Funkcja popytu:
jest ściśle malejąca,
ma pochodną,
jej pochodna jest ujemna D`(p) < 0.
Zakładamy
zwykle więcej:
![]() .
Oczywiście:
.
Oczywiście:
![]() takie, że
takie, że
![]() ;
piszemy
;
piszemy
![]() .
.
- dla każdego
- istnieje dokładnie
jedno
![]()
Istnieje więc funkcja odwrotna D-1 do funkcji popytu D, zwana odwrotną funkcją popytu rynkowego.
D-1: „ilość Q” „cena p płacona przez konsumentów, gdy na rynku dostępnych jest Q jednostek towaru”.
p – cena rynkowa
Elastyczność cenowa popytu przy cenie p:
![]() ; Oznaczana
też przez (epsilon); zawsze
< 0.
; Oznaczana
też przez (epsilon); zawsze
< 0.
Zmiana popytu przy zmianie ceny:
![]()
zmiana popytu wywołana „małą” zmianą ceny o p.
![]() ,
,
czyli
to samo, co
![]() .
.
Popyt jest:
elastyczny, gdy
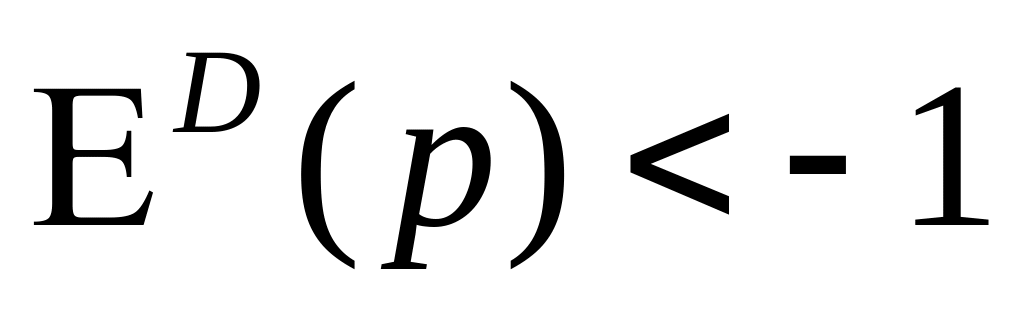
nieelastyczny, gdy
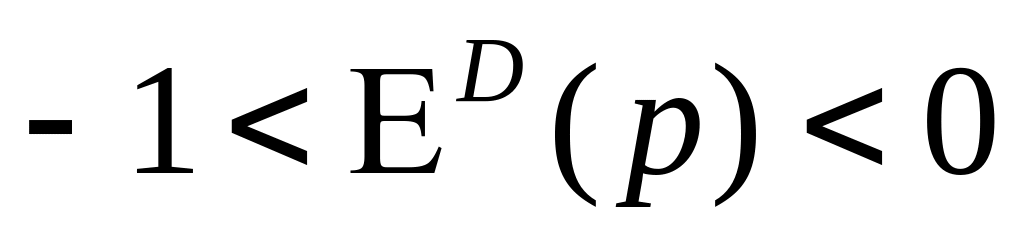
jednostkowo elastyczny, gdy
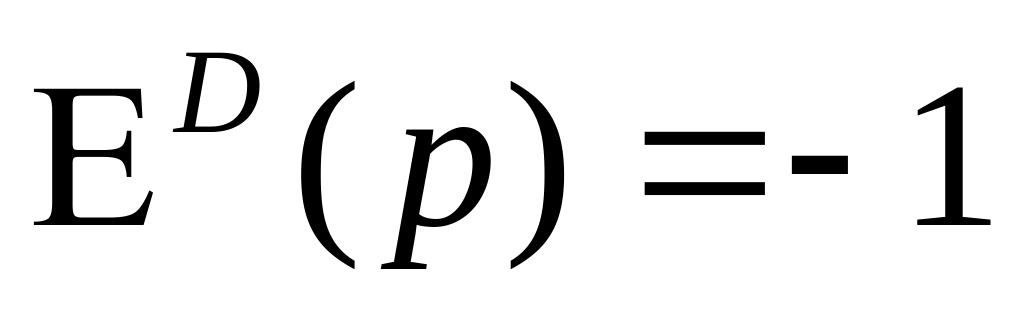 -
procentowe zmiany ceny i popytu są identyczne
-
procentowe zmiany ceny i popytu są identyczne
Determinanty elastyczności cenowej [wg SM]:
niezbędność towaru
dostępność substytutów
udział wydatków na towar w ogólnych wydatkach konsumentów
czas dostosowań
Elastyczność odwrotnej funkcji popytu D-1:
![]()
Ponieważ Q = D(p) oraz Q + Q = D(p + p), dla stosowanego p i („małego”) p, to
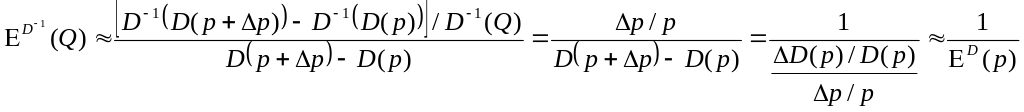 .
.
Czyli
![]() ,
gdzie
.
,
gdzie
.
Aby określić elastyczność odwrotną f. popytu, wystarczy określić odwrotność elastyczności cenowej popytu (która jest jej odwrotnością).
Zależność przychodu od elastyczności ceny zbytu
![]() ,
czyli:
,
czyli: ![]()
Jest to elastyczność ceny zbytu P względem ilości q.
![]() (bo
cena P jest nierosnącą funkcją q)
(bo
cena P jest nierosnącą funkcją q)
Przychód krańcowy:
![]()
Gdy wyrażenie w nawiasie […]:
> 0 – przychód R rośnie
< 0 – maleje
gdy R maksymalne – przychód R jest zerowy (= 0 – p. k. zerowy – maksimum funkcji – przychód maksymalny)
Wniosek: Firma maksymalizująca przychód R wybiera poziom produkcji qrev tak, aby:
![]()
qrev – poziom produkcji maksymalizujący przychód
Uwagi:
Ww. warunek oznacza, że małe procentowo zwiększenie (zmniejszenie) ilości towaru prowadzi do (prawie) identycznego procentowego obniżenia (odpowiednio podwyższenia) ceny.
Zwiększając (zmniejszając) poziom produkcji ponad qrev zmniejszamy (odp. zwiększamy) zysk. [Uzasadnienie:
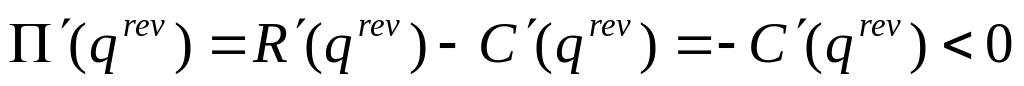 ,
a więc dla
,
a więc dla
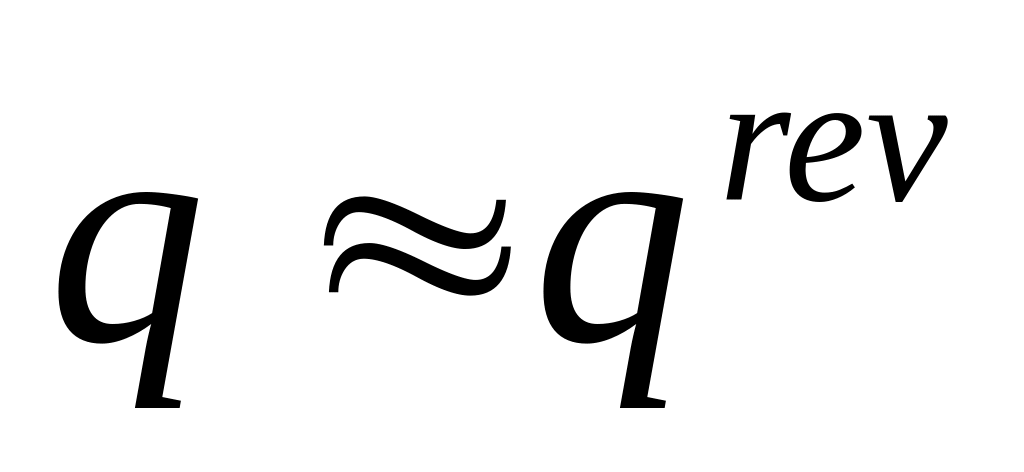 zysk
zysk
 jest malejącą (ściśle) funkcją ilości
jest malejącą (ściśle) funkcją ilości
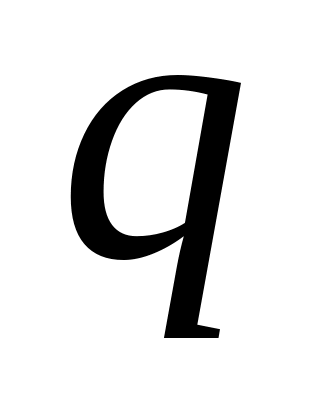 .]
.]Niech
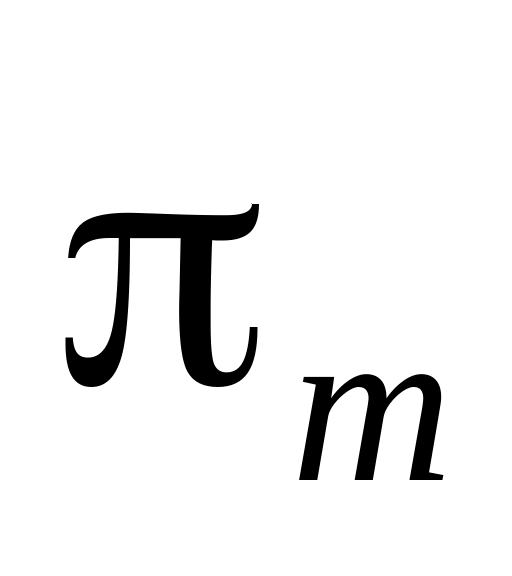 będzie zyskiem wymaganym w modelu maksymalizacji przychodów ze
sprzedaży W. J. Baumola.
Jeśli
będzie zyskiem wymaganym w modelu maksymalizacji przychodów ze
sprzedaży W. J. Baumola.
Jeśli
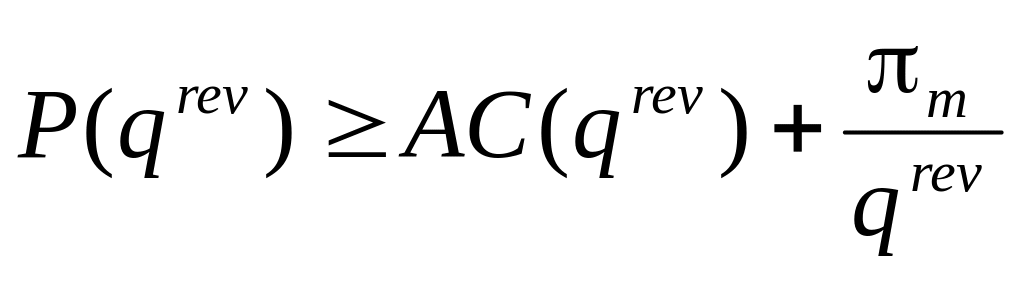 ,
to
,
to
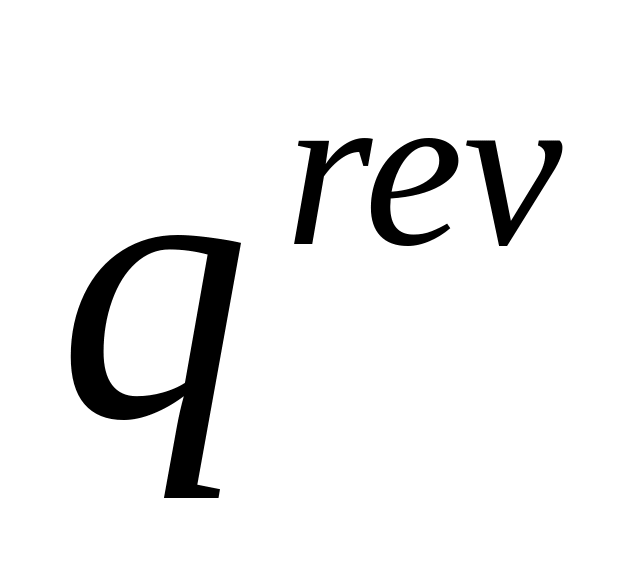 jest optymalnym poziomem produkcji dla ww. modelu firmy.
jest optymalnym poziomem produkcji dla ww. modelu firmy.
![]() - warunek, aby zysk był
0 (aby nie było strat)
- warunek, aby zysk był
0 (aby nie było strat)
![]() - warunek, aby maksymalizować przychód (?)
- warunek, aby maksymalizować przychód (?)
Maksymalizacja zysku
- poziom produkcji maksymalizujący zysk firmy
![]()
Warunek
konieczny maksymalizacji zysku
![]() zachodzi
zachodzi
![]() .
.
Oczywiście wyrażenie w nawiasie […] musi być > 0. Stąd
Wniosek:
Jeśli firma maksymalizuje zysk
,
to jej poziom produkcji
musi spełniać warunek
![]() .
.
Uwagi:
To nie jest równoważne warunkowi koniecznemu, tylko z niego wynika!
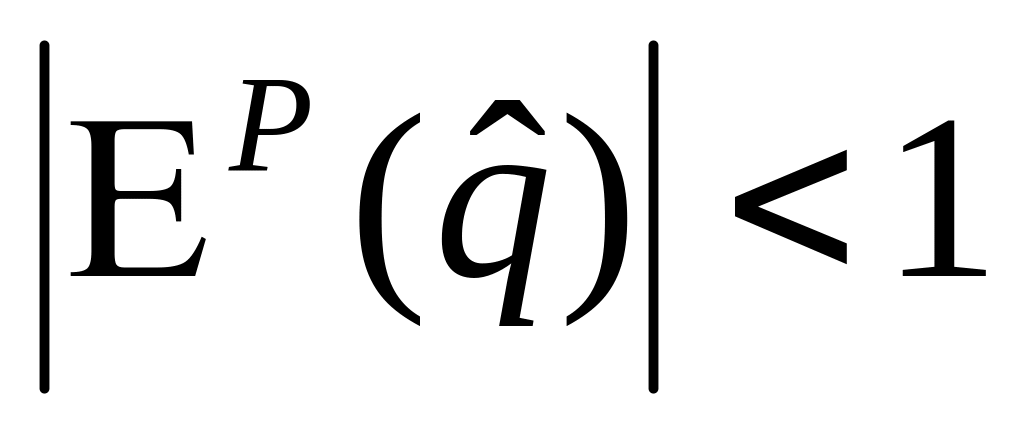 .
Czyli dla poziomów produkcji
.
Czyli dla poziomów produkcji
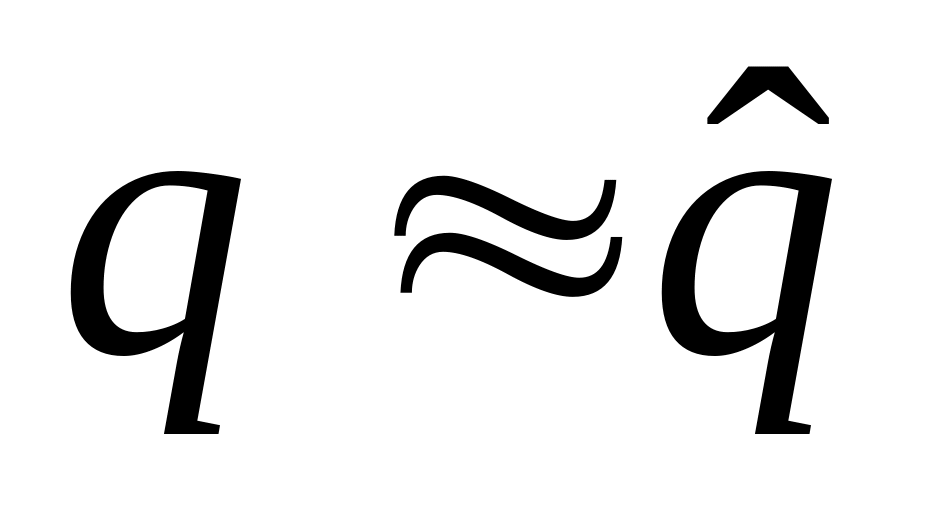 ,
,
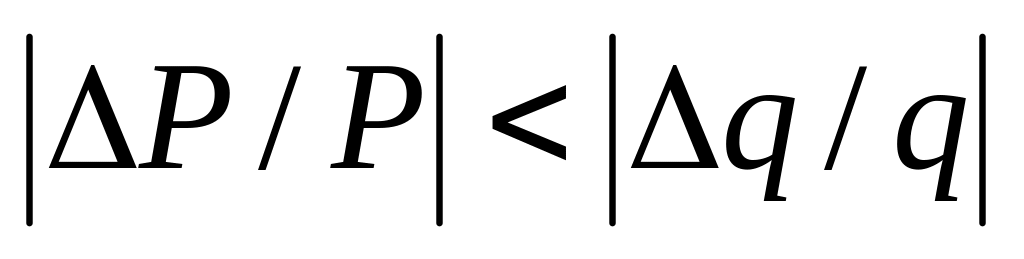 .
.
Inna forma warunku koniecznego:
![]() .
.
Dla firmy maksymalizującej zysk indeks Lernera L jest równy wartości bezwzględnej elastyczności ceny zbytu P względem ilości q.
W
szczególności:
![]() oraz
oraz
![]() .
.
[Zawsze, jeśli firma maksymalizuje zysk, cena, którą uzyskuje za jednostkę towaru równa się co najmniej kosztowi krańcowemu.]
MONOPOL ZWYKŁY MAKSYMALIZUJĄCY ZYSK
„Jeden sprzedawca” (firma) na rynku rozpatrywanego towaru;
istotne bariery wejścia na rynek (a także mobilności i wyjścia);
brak bliskich substytutów towaru (w tym efekt „sieci” i „zamknięcia pod kluczem”).
Rynek właściwy (levar market) – pojęcie odwołujące się do tego, co jest faktyczne.
Monopol – trwała sytuacja rynkowa, tylko jeden dostarczyciel danego dobra lub usług. Firma może być monopolistą na jednym rynku, a na drugim już nie.
Zwykle zakładamy, że jest wielu nabywców towaru. Cena jest jednakowa dla wszystkich.
Bariery wejścia – korzyści skali (ogromna przewaga monopolisty, który dużo produkuje), bariera kapitałowa, przewaga kosztowa lub jakościowa monopolisty, dostęp do nakładów, bariery prawne, reakcja monopolisty (predatory pricing np).
Bariery wyjścia i mobilności – w innych „przemysłach” redukują potencjalną konkurencję. Bariery te wynikają z istnienia bezpowrotnie utraconych nakładów.
Zwykły (in. czysty) monopol – brak potencjalnej konkurencji. Brak potencjalnej konkurencji umożliwia jednocześnie istnienie „przemysłów” o różnej rentowności.
(brak firm chętnych do wejścia na rynek)
Teoria rynków spornych – contestable markets:
monopolista zachowujący się, jak firma w warunkach konkurencji doskonałej ze względu na istnienie potencjalnej konkurencji.
Efekt sieci – kupują produkt, bo „wszyscy” go mają (np. system operacyjny Microsoft)
Lock-in – konsola A, gdy firmy A.
Przypomnienie:
Maksymalizujący
zysk poziom produkcji
dowolnej firmy opisanej funkcją kosztu C i ceną zbytu P wyznaczamy
z warunku:
![]() .
.
Cena „monopolowa”
Monopol: ilość q produkowana przez monopolistę = całkowitej ilości towaru dostępnej na rynku!
Czyli Q
= q, a
.
Stąd dla monopolisty cena
![]() .
.
Cena zbytu monopolisty określona jest jednoznacznie przez funkcję popytu rynkowego.
Monopolista jest cenotwórcą („price maker”).
Monopolista ma pełną kontrole nad ceną. Cena wynika z krzywej popytu.
Przypomnienie – relacja między ceną zbytu a elastycznością funkcji popytu:
, gdzie .
Cena
![]() na rynku monopolistycznym spełnia
na rynku monopolistycznym spełnia
![]() .
cena
dla
.
cena
dla
maksymalizacji zysku
Wnioski dotyczące monopolisty maksymalizującego zysk:

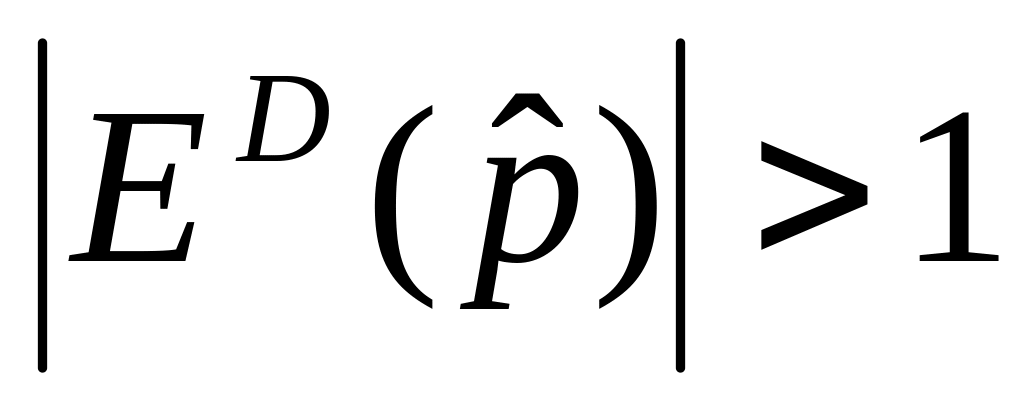 - monopolista „pracuje” na elastycznej części krzywej popytu;
- monopolista „pracuje” na elastycznej części krzywej popytu;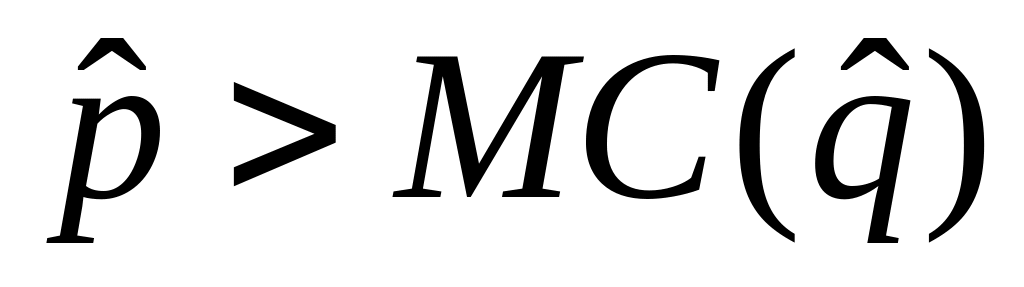 - cena „monopolowa” jest wyższa od kosztu krańcowego, bo
- cena „monopolowa” jest wyższa od kosztu krańcowego, bo
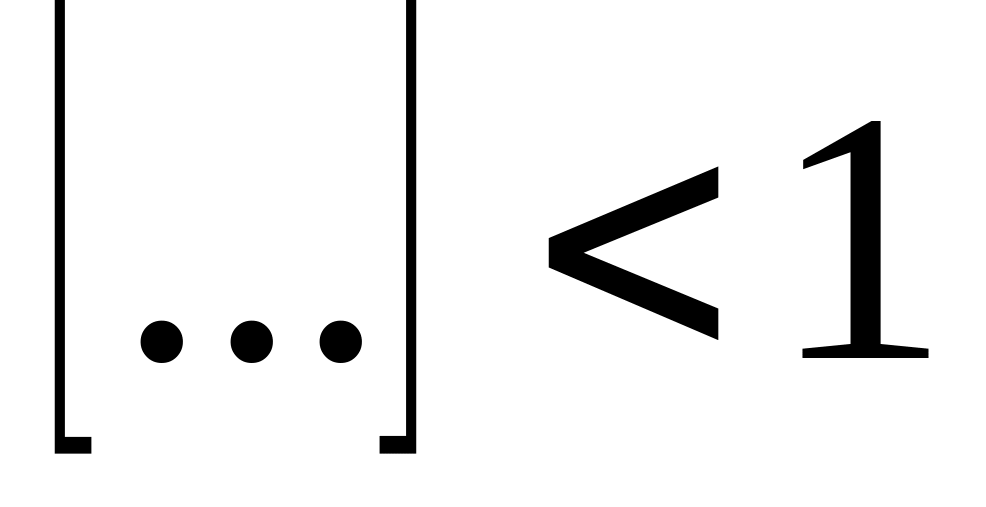 ;
;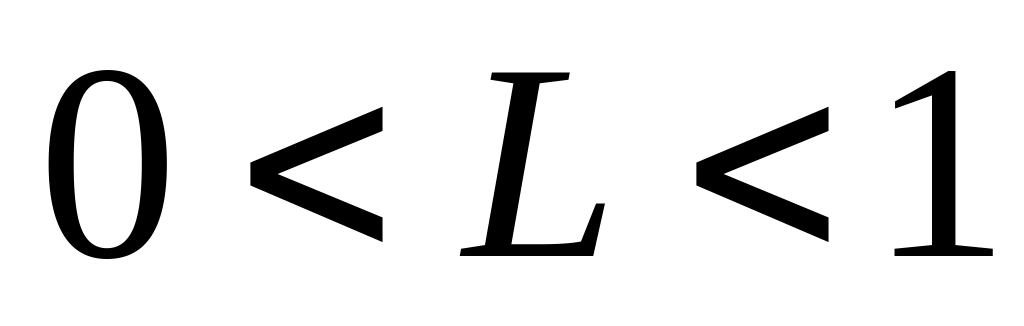 ,
gdzie L oznacza indeks Lernera (L > 0 bo cena wyższa od kosztu
krańcowego);
,
gdzie L oznacza indeks Lernera (L > 0 bo cena wyższa od kosztu
krańcowego);Zysk maksymalny
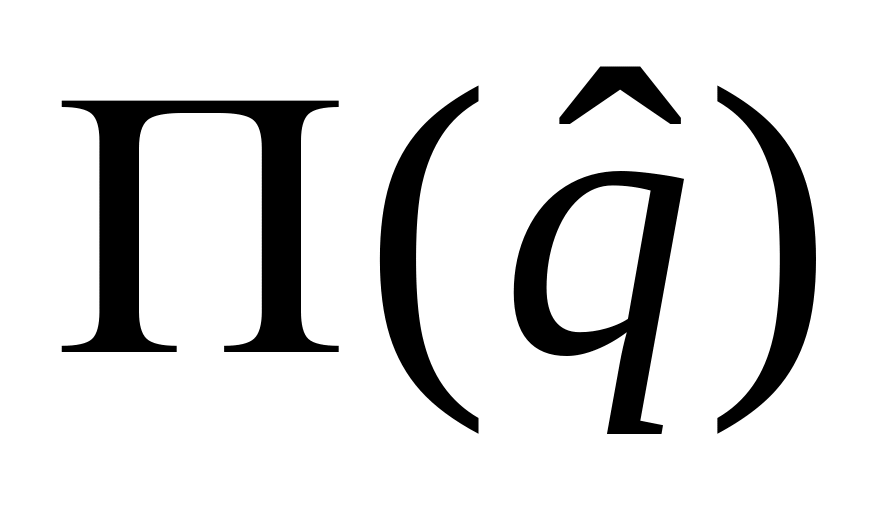 jest dodatni
jest dodatni
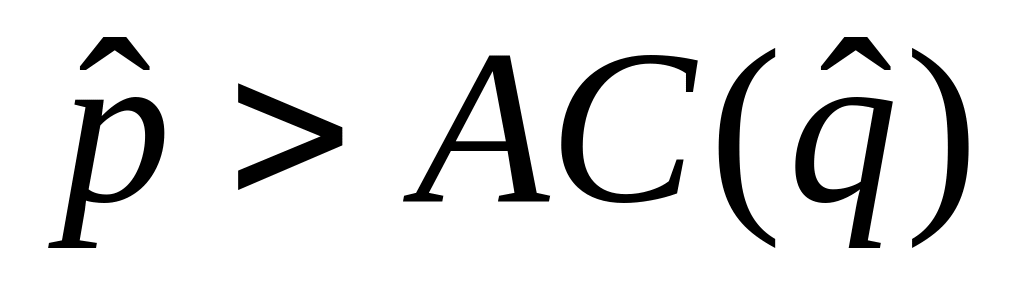 ;
;Zmniejszając wówczas trochę cenę (i zwiększając produkcję), monopolista też miałby ciągle zysk dodatni.
Najważniejsze punkty 1-3.
OLIGOPOL
Założenia ogólne:
Rozpatrujemy m firm wytwarzających identyczny produkt.
Poniżej: m = 2 – duopol, dla uproszczenia.
Decyzja każdej firmy ma na cenę wpływ bezpośredni oraz pośredni związany z reakcjami konkurentów.
Cel (neoklasyczny) każdej firmy – maksymalizacja swojego zysku.
Formy oligopolu:
oligopol Cournot
oligopol Bertranda
przywództwo cenowe
przywództwo jakościowe (Stackelber)
kartel (zmowa)
i inne.
Funkcja popytu rynkowego
- dla każdego
- istnieje
- istnieje dokładnie
jedno
R++
- zbiór liczb dodatnich (>0)
D: R++ R++ funkcja popytu („rynkowego”)
„cena p” „ilość q, którą konsumenci po cenie p kupią”
Zakładamy p. popytu w wersji różniczkowej (f.
odwrotna):
![]() .
.
Stąd
![]() ,
takie że
,
takie że
![]() ,
a więc istnieje funkcja odwrotna do f. popytu
,
a więc istnieje funkcja odwrotna do f. popytu
![]() ;
;
f. D-1 ma pochodną i
![]() .
.
Oznaczenie:
![]() odwrotna funkcja popytu
odwrotna funkcja popytu
![]() ,
którą konsumenci płacą, gdy na rynku jest q jednostek towaru.
,
którą konsumenci płacą, gdy na rynku jest q jednostek towaru.
Zakładamy:
koszty krańcowe firm są dodatnie, tzn.
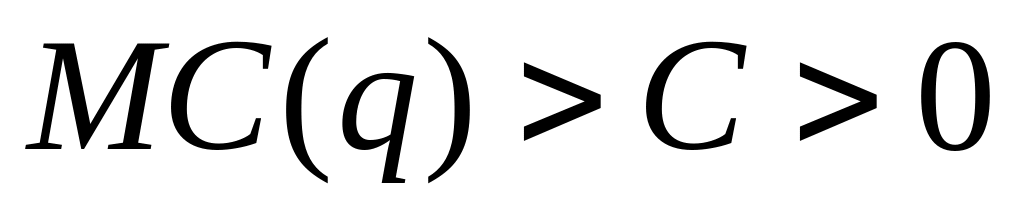 ,
,przychód dąży do zera, gdy
 lub
lub
 ,
tzn.
,
tzn.
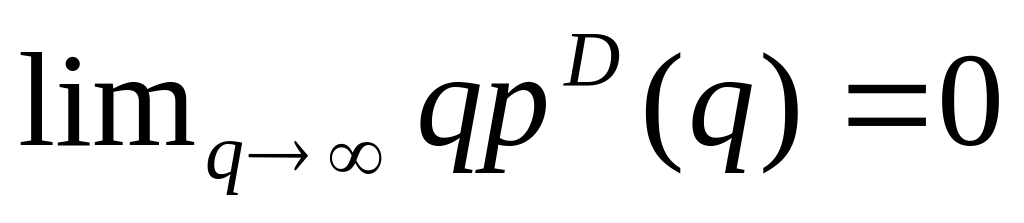 oraz
oraz
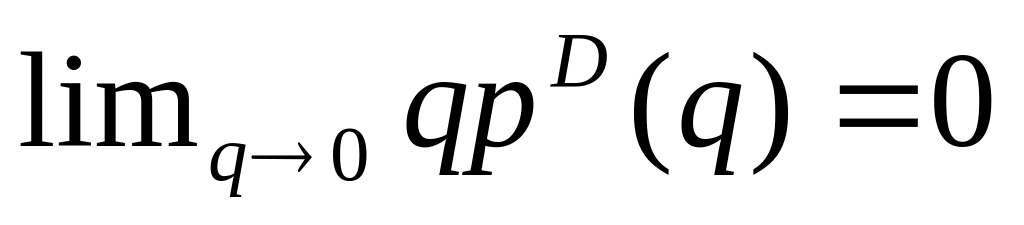 .
.
