Распределение случайной величины по закону Вейбулла
Распределение Вейбулла представляет собой двухпараметрическое распределение. Закон Вейбулла удовлетворительно описывает распределение наработки до отказа подшипников, элементов радиоэлектронной аппаратуры, его используют для оценки надежности деталей и узлов машин, в частности автомобилей, а также для оценки надежности машин в процессе их приработки.
Широкое применение закона Вейбулла объясняется тем, что этот закон является универсальным, т.к. он может описывать процессы с распределениями: нормальным, логарифмически нормальным, экспоненциальным и др.
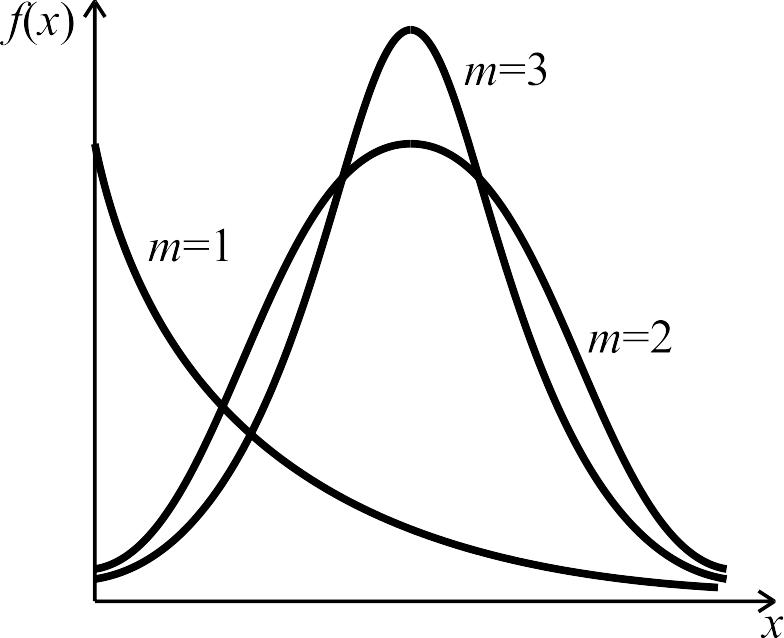
Плотность распределения выражается зависимостью вида:
где m – параметр формы кривой распределения; t0 – параметр масштаба.
Функция распределения (вероятность отказа) описывается соотношением:
Вероятность безотказной работы:
Подбирая значения параметров m и t0 , можно получить лучшее соответствие расчетных значений опытным данным по сравнению с нормальным и экспоненциальным законами.
Для изделий, у которых имеются скрытые дефекты, но которые длительное время не стареют, опасность отказа имеет наибольшее значение в начальный период, а потом быстро падает. Вероятность безотказной работы для такого изделия хорошо описывается законом Вейбулла с параметром m<1. И наоборот, если изделие хорошо контролируется при изготовлении и почти не имеет скрытых дефектов, но подвергается быстрому старению, то функция надежности описывается законом Вейбулла с параметром m>1. При m=3,3 распределение Вейбулла близко к нормальному. При m=1 распределение Вейбулла становится экспоненциальным.
Отказоустойчивые системы
Способность систем сохранять свою работоспособность при отказе одного или нескольких элементов называется отказоустойчивостью (толерантностью). По способу обеспечения отказоустойчивости все системы делятся на системы типа «m из n», мостиковые и комбинированные.
Система типа “m из n” сохраняет свою работоспособность, если из n ее элементов работоспособными окажутся любые m и более элементов. Вариантами систем типа “m из n” являются последовательные и параллельные системы.
Последовательная система – это система типа “n из n”. Отказ любого элемента этой системы приводит к отказу всей системы. Поэтому последовательная система не является отказоустойчивой. Примером последовательной системы служат: последовательно соединенные электрические лампы; система подшипников.
Параллельная система – это система типа “1 из n”. Отказ параллельной системы наступает при отказе всех ее элементов. Примером параллельной системы служат: параллельно соединенные электрические лампы; резервированные системы.
Мостиковая система получается из параллельно соединенных друг с другом последовательных цепочек элементов посредством присоединения диагональных элементов между узлами различных параллельных ветвей (рис.1.7). Работоспособность такой системы нарушается при возникновении определенной комбинации отказов ее элементов.
Комбинированная система – это система, состоящая из подсистем типа «m из n» и мостиковых подсистем. Для отказа такой системы необходимо возникновение определенной комбинации отказов. Примеры: смешанно соединенные электрические лампы; частично резервированные системы.