2. Вычисление длины дуги кривой

Пусть кривая на плоскости задана уравнением у = f ( x ) или х =  ( у ). На кривой выбраны точки А и В с координатами: А(а; с), В(b; d). Длина l дуги от точки А до точки В вычисляется по формуле:

l = или l = .

Если кривая задана параметрическими уравнениями , t [t₁; t₂], то

длина дуги вычисляется по формуле l = .

Если кривая задана уравнениями в полярных координатах r = r ( φ ), α ≤ φ ≤ β,

то длина дуги кривой вычисляется по формуле l = .

Пример 1. Вычислить длину дуги кривой y = ln sin x от х = до х = π.

Предварительно вычислим : y = ln sin x, y′ = ,

= = , т.к. ≤ х ≤ π. Следовательно, l = = ln = ln – ln = 2ln .

Пример 2. Вычислить длину дуги астроиды x = a cos³t , y = a sin³t (см. рис. к задаче 27)

Найдем сначала ¼, т.е. длину дуги кривой, лежащей в I четверти:

= = =

= = = 3a =

= 3a = 3a = a. Следовательно, l = 6a.

Пример 3. Найти длину кардиоиды r = a (1 + cosφ).

Найдем сначала половину длины кривой: = =

= = a = a =

= a = –4a cos = –4a (0 – 1) = 4a. Значит, l = 8a.

3.3. Вычисление объемов тел

3.3.1. Вычисление объема тела по известным площадям поперечных сечений

Пусть в пространстве задано тело. Пусть построены

его сечения плоскостями, перпендикулярными оси Ох.

Площадь фигуры, образующейся в сечении, зависит от

точки х, определяющей плоскость сечения. Пусть эта

зависимость известна и задана непрерывной на [a, b]

функцией S (x). Тогда объем части тела, находя-

щейся между плоскостями х = а и х = b вычисляется

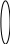
п о формуле

3.3.2. Объемы тела вращения,

образованного вращением вокруг оси

Ох ( или оси Оу) криволинейной трапеции,

ограниченной кривой y = f (x) (f (x) ≥ 0) и

прямыми y = 0, x = a, x = b, вычисляются

с оответственно по формулам: , .

Если тело образуется при вращении вокруг оси Оу криволинейной

трапеции, ограниченной кривой х = j (у) (j (у) ³ 0) и прямыми

х = 0, у = с, y = d, то объем тела вращения равен .

Пример 1. Н айти объем V пирамиды с площадью основания Q и высотой H.

Направим ось Ох перпендикулярно основанию пирамиды, а начало координат совместим

с вершиной О данной пирамиды. На расстоянии х от точки О проведем поперечное сечение

пирамиды. Его площадь обозначим через S, она является функцией от х: S = S (х).

Площади поперечного сечения (параллельного основанию) и основания относятся как

квадраты их расстояний от вершины, т.е. . Отсюда S (х) = х².

Следовательно, V = Q ∙H.

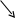
Пример 2. Найти объем тела, ограниченного поверхностями x² + 4y² = 1, z = x (x  0), z = 0.

В результате пересечения эллиптического цилиндра x² + 4y² = 1 плоскостями z = x и

z = 0 получим тело, изображенное на рисунке. Сечение тела, перпендикулярное оси Ох,

проведенное на расстоянии х от начала координат представляет собой прямоугольник ABCD.

Найдем его площадь S = S (х). Высота (ширина) MN прямоугольника равна х, т.е. | MN | = х

(в прямоугольном треугольнике NMO угол  NOM равен 45) . Точка D (x; y) лежит на эллипсе

x² + 4y² = 1. Значит, MD = y = , т.е. | MD | = => S(x) = AD ∙ MN =

2 MD ∙ MN = 2 ∙ ∙ x = x ∙ .

Следовательно, V = = – =

Пример 3. Найти объем тела, ограниченного двумя цилиндрами x² + y² = R² и x² + z² = R².

Изобразим на рисунке восьмую часть тела, расположенную в I октанте. В поперечном

сечении (перпендикулярном оси Ох) тела получится квадрат. Его сторона а равна ординате

т очки М (х; у), лежащей на окружности x² + y² = R² , т.е. S(x)= = R² – x².

С ледовательно,

Задание для самостоятельного решения

1. Найти объем шара радиуса R.

2. Найти объем конуса с радиусом основания R и высотой Н.

3. Найти объем тела, ограниченного параболическим цилиндром z = x² , плоскостями у = 0,

у = 6, z = 1.

4. Найти объем тела, ограниченного параболическим цилиндром z = 1 – y² , плоскостями у = 0,

z = 0, x = 0, x = 12.

5. Найти объем тела, ограниченного параболоидом z = x² + y² и плоскостью z = 4.

6. Найти объем эллипсоида x² + y² + 4z²  4.

7. Найти объем шарового слоя, вырезанного из шара x² + y² + z² = 25 плоскостями у = 1 и у = 4.

8. Найти объем тела, ограниченного однополостным гиперболоидом x² + y² / 4 – z² = 1 и плоскостями z = 0, z = 3.

9. Найти объем тела, ограниченного эллиптическим параболоидом x² / 9 + y² / 3 = z и плоскостью z = 4.

10. Найти объем обелиска, параллельные основания которого квадраты со сторонами a и b (a < b), высота равна h.

11. Найти объем тела, ограниченного конической поверхностью (у – 3)² = x²/ 2 + z ² / 3 = z и плоскостью у = 1.

12. Цилиндр, основанием которого служит эллипс 4x² + 25y² = 400, пересечен наклонной плоскостью, проходящей через малую ось эллипса. Высота полученного “цилиндрического клина” равна 5. Найти его объем.

13. Найти объем шарового сегмента высотой 2, отсеченного от шара радиуса 4.

14. Найти объем тела, ограниченного плоскостями z = 1, z = 4, если площадь его поперечного сечения обратно пропорциональна квадрату расстояния сечения от начала координат, а при z = 3 площадь сечения S(z) = 20.

Пример 4. Найти объем тела, образованного вращением фигуры, ограниченной линиями ху = 6, х = 1, х = 4, у = 0, вокруг оси Ох и вокруг оси Оу.

Пример 5. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями y = e^–x, x = 0,

y = 0 (x  0).

y = e^–x => x = –ln y => V_y = π = π = =

= = = = –2π (0 – 1) = 2π.

Пример 6. Найти объем тела, образованного вращением вокруг оси Оx арки циклоиды , 0 ≤ t ≤ 2π.

V_x = π = π = πa³ =

= πa³ = πa³ =

= πa³ = πa³ =

= πa³ πa³∙ 5 π = 5π²a³.

Пример 7. Найти объем тела, образованного вращением вокруг прямой х = – 2 области, ограниченной линиями

у = x³ , х = –1, х = 0, y = 4 .

Перенесем начало координат в точку О₁(–2; 1), сохранив направления осей (рис.) . В новой

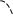
с истеме координат уравнение кубической параболы примет вид у = (х₁ – 2)³ => х₁ = 2 + .

Объем V_н нижней части тела (под осью Ох) найдем как разность двух объемов V_н = V₁ – V₂ ,

где V₂ = π = π , V₁ = π = π (или как объем цилиндра с высотой 1 и

радиусом основания 1). Имеем: V_н = π – π = π. Объем V_в верхней части тела (над

осью Ох), очевидно, равен V_в = 12π (как разность объемов круговых цилиндров:

V = π ∙ 4 ∙ 4 – π ∙ 1 ∙ 4 = 12π ). Т.о. V = V_н + V_в = π + 12 π = π.

Пример 8. Найти объем тела, образованного вращением вокруг оси Ох фигуры,

ограниченной графиками функций у = 2х – х², у = –х + 2.

Графики функций (см. рис.) пересекаются в точках (1; 1) и (2; 0) =>

=> V = – = =

= = = .

Задание для самостоятельного решения

Найти объем тела, образованного вращением фигуры, ограниченной линиями:

15. у = х³, х = 0, у = 8 вокруг оси Ох.

16. у = , у = 0, х = 0, х = 1 вокруг оси Ох.

17. у² = (х + 1) ³, х = 0 вокруг оси Оу.

18. у² = 16 – х, х = 0 вокруг оси Оу.

19. у = е ^х, х = 0, х = ln 2 вокруг оси Оx.

20. у = 2 sin x, 0 ≤ х ≤ π вокруг оси Оx.

21. у² = 4x, у² = х ³ вокруг оси Оx.

22. x² + у² = 1 вокруг прямой x = 2.

23. 2у = x² + 4х + 4, у = 2 вокруг оси Оу.