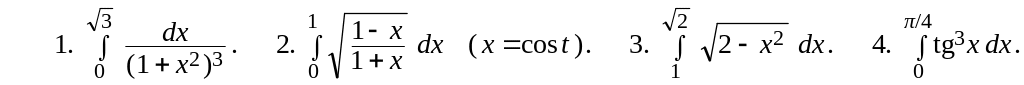Определенный и несобственные интегралы
Приемы вычислений определенного интеграла
1.1. Основные понятия и свойства
Пусть функция у = f ( x ) определена на отрезке [a, b] и на этом отрезке произвольно выбраны точки x0, x1, … , xn, так что a = x0 < x1 < … < xn = b, т.е. выбрано произвольное разбиение отрезка [a, b] на n частей. В каждом интервале
(xi
– 1; xi
] опять
же произвольно выбрана точка сi
, i
= 1, 2, … , n.
Сумма вида
,
где Δxi
=
xi
–
xi
– 1,
называется
интегральной суммой функции
f ( x ) на отрезке [a, b].
Определенным
интегралом от
функции
f
(
x
)
на отрезке
[a,
b]
называется
предел интегральных сумм
Sn
при
условии,
что длина
наибольшего частичного отрезка
Δxi
стремится
к нулю:
=
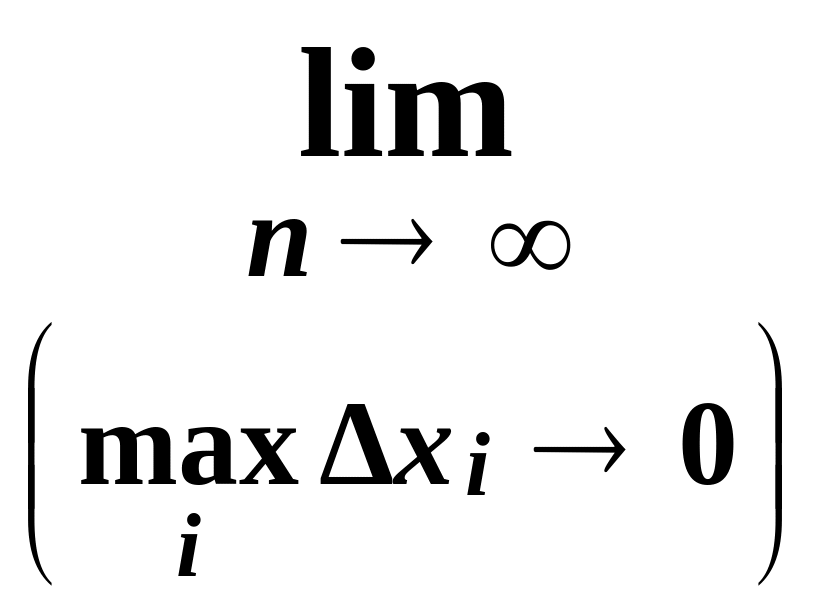
(1)
Теорема существования определенного интеграла. Если функция f ( x ) непрерывна на отрезке [a, b], то предел (1) существует и не зависит ни от способа разбиения отрезка [a, b], ни от выбора точек сi .
Функция f ( x ) в этом случае называется интегрируемой на отрезке [a, b].
Более того, если функция f ( x ) ограничена отрезке [a, b] и непрерывна в нем, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
Основные свойства определенного интеграла
= –
;
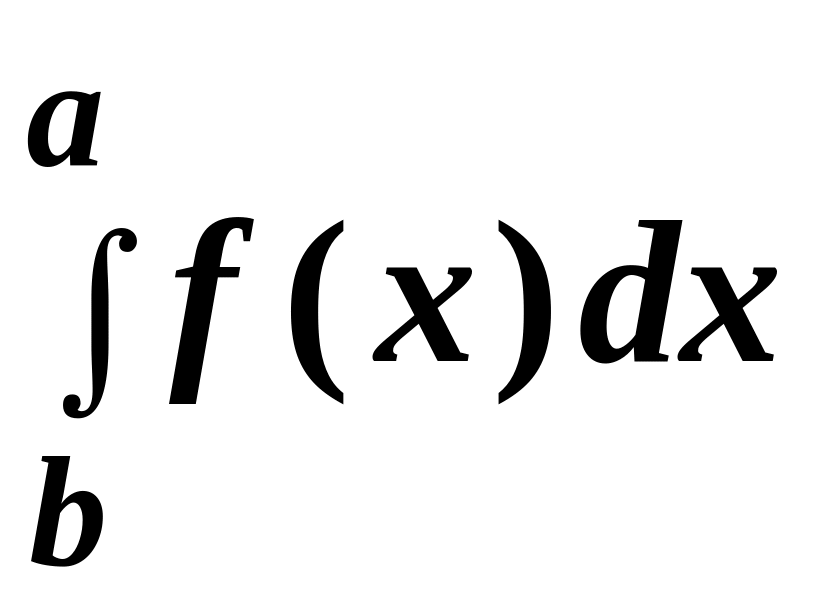2.
= 0;
3.
= α
± β
;
4.
=
+
,
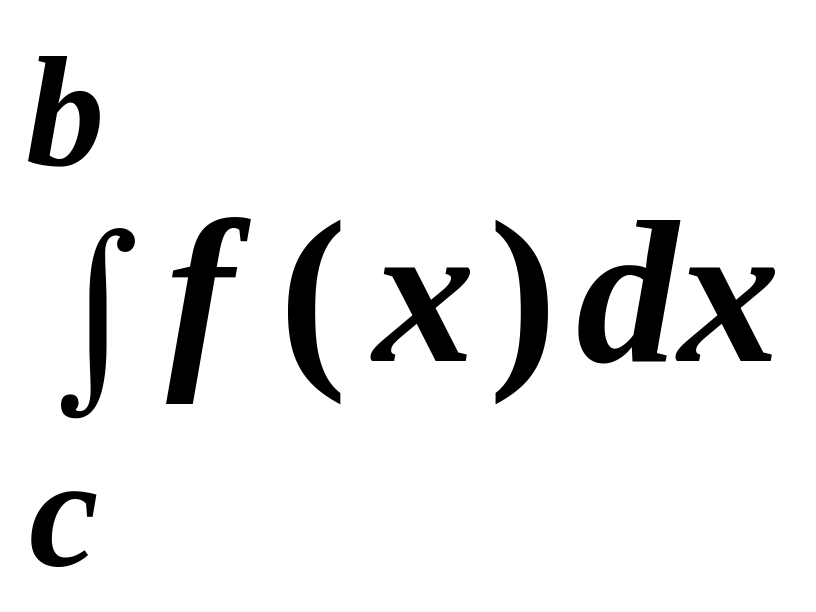a
< c
< b;
5. ≥ 0, если f ( x ) ≥ 0 на [a, b], ≤ 0, если f ( x ) ≤ 0 на [a, b];
6. Если f ( x ) ≤ g ( x ) на [a, b], то ≤ ;
7. Если М – наибольшее, m – наименьшее значение f ( x ) на [a, b], то
m (b – a) ≤ ≤ M (b – a);
8. теорема
о среднем:
= f
(
c
)
(b
– a),
c
[a,
b]
;
9.
≤
;
10.
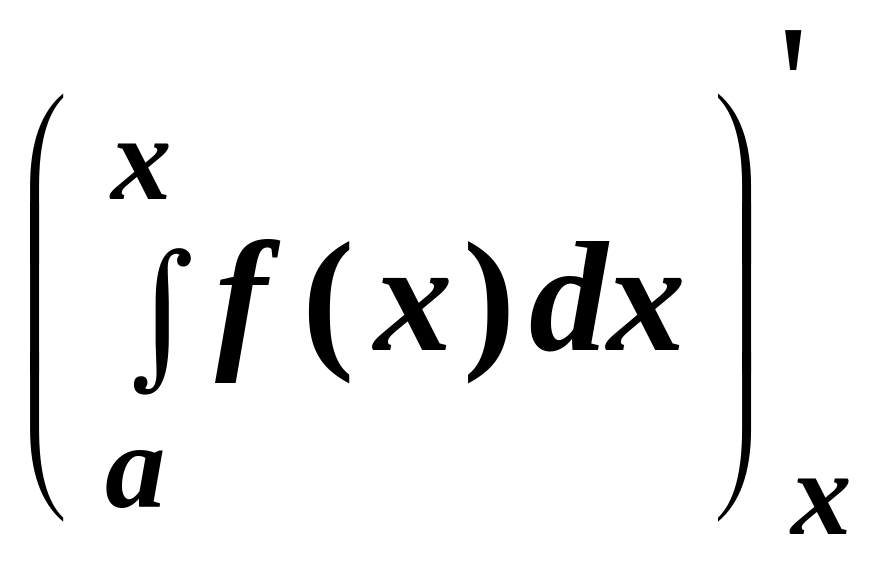= f
(
x
).
1.2. Формула Ньютона – Лейбница
=
= F(b)
– F(a)
При интегрировании четных и нечетных функций в симметричных пределах интегрирования полезно использовать формулу
=
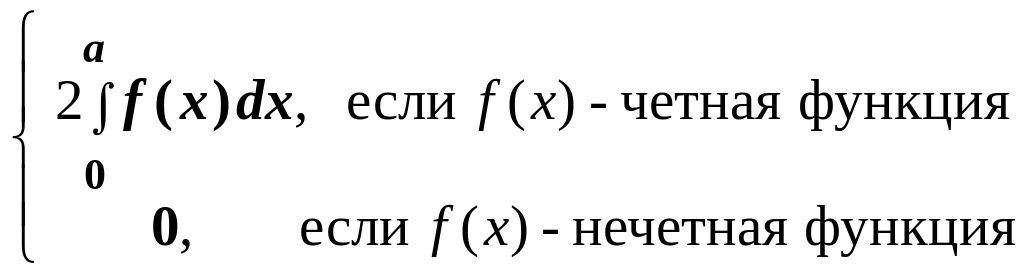
Примеры.
1.
=
=
–
= 21 .
2.
=
=
=
= arcsin 0 –
=
.
Примеры.
3.
=
=
+
=
=
+
=
–
0 –
=
–
=
.
Примеры.
4.
= ||
=
||
+
+
+
=> x4
+ 1 = (C
+ D)
x4
+ (B
+ E)
x3
+ (A
+ C)
x2
+ B
x
+ A
=>
=>
=>
=>
=
||
–
+
|| =
=
=
= –
+
–
ln2 + ln5 – ln2 = ln
+
.
Примеры.
5. Найти значение
интеграла
,
если f(x)
=
=
+
=
+
=
e
– 1 + 4 – 2 = e
+ 1.
Замена переменной в определенном интеграле
Пусть для
вычисления интеграла
сделана подстановка x
=
( t
). Если
функция
( t
) и
ее производная
′
( t
) непрерывны
на отрезке [α;
β],
причем
а = (α ) и b = (β), (1)
то справедлива
формула:
=
.
(2)
Формула (2) называется формулой замены переменной интегрирования в определенном интеграле.
Отметим:
функцию x = ( t ) следует подбирать так, чтобы, подставив ее вместо х в подынтегральное выражение, получился более простой интеграл;
новые пределы интегрирования находить из соотношений (1);
в отличие от неопределенного интеграла при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;
иногда удобнее делать подстановку не x = ( t ), а t = ( x ).
Не существует общего «рецепта», следуя которому можно всегда понять, какую подстановку надо применить к данному интегралу. Однако следует иметь в виду следующие полезные подсказки:
1)
если под знаком интеграла стоит сложная
функция f
(
(x)),
то, как правило, используется подстановка
t
=
(
x
). Например, если в подынтегральном
выражении встречается функция sin
(1/x),
то стоит попробовать подстановку t
=
1/x,
а если
-
то t
= x2
и т.д.
2)
если в подынтегральном выражении есть
готовый дифференциал функции
(x),
т.е. выражение (x)
dx,
то имеет смысл попробовать подстановку
t
=
(
x
). Поэтому целесообразно запомнить
следующие формулы для наиболее часто
встречающихся дифференциалов:.
Примеры.
6.
=
||
||
=
=
=
=
=
–
5∙
ln|
2
=
3 – 1 –
(
ln11
– ln7
) = 2 –
ln
.
Примеры.
7.
= ||
||
=
=
=
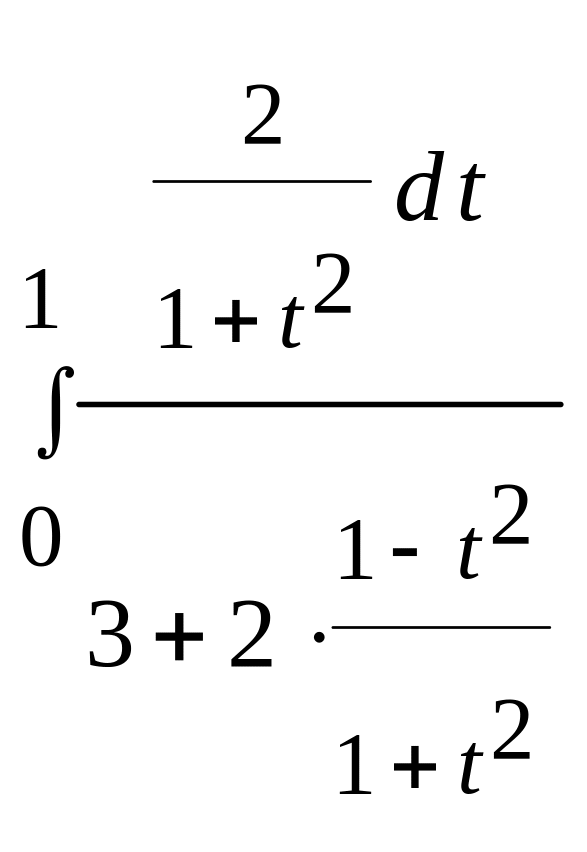dt
=
=
arctg
.
8.
=
||
||
=
=
=
=
=
–
+
=
.
Задание для самостоятельного решения
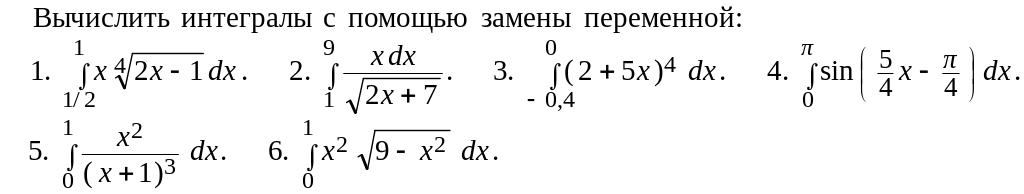
9.
=
||
||
=
=
–
=
=
=
ln
=
ln
.
10.
=
||
||
=
=
=
=
=
=
=
=
.
Задание для самостоятельного решения
