Задача 3

Рассмотрим два комплексных числа в тригонометрической форме

и .

Найдем произведение и частное этих комплексных чисел.

При перемножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются, т.е.

.

При это равенство принимает вид:

и носит название формулы Муавра.

Отсюда следует формула возведения комплексных чисел в натуральную степень

.

Деление комплексных чисел, заданных в тригонометрической форме, выполняется по формуле

.

Модуль частного равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя.

В результате умножения и деления чисел может получиться аргумент произведения и частного, не являющийся главным значением.

Умножение, деление, возведение в целую положительную степень для комплексных чисел, заданных в показательной форме, выполняются по формулам:

,

,

Пример

Даны числа .

Вычислить .

Решение.

Задача 4

Рассмотрим задачу извлечения корня из комплексного числа, заданного в тригонометрической форме: . Чтобы извлечь корень из комплексного числа, нужно извлечь корень (арифметический) той же степени из модуля данного числа, а аргумент разделить на показатель корня:

.

Учитывая периодичность тригонометрических функций, следует отметить, что выражение принимает только n различных значений. Формула извлечения корня из комплексного числа в тригонометрической форме имеет вид

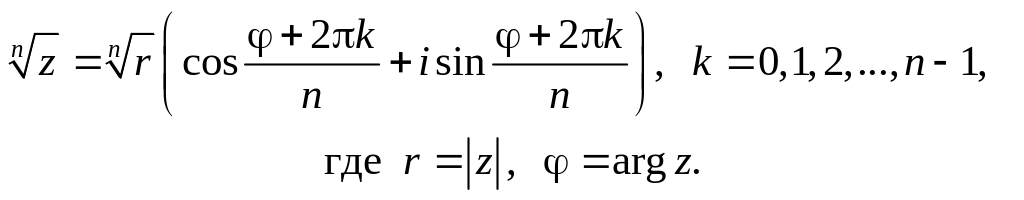(1)

Задача извлечения корня степени n из комплексного числа равносильна решению уравнения вида

.

Для решения уравнения нужно найти и использовать формулу извлечения корня. Исследование формулы (1) показывает, что точки, соответствующие значениям , расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой . Аргументы двух последовательных чисел отличаются на , т.е. каждое следующее значение может быть получено из предыдущего поворотом радиус-вектора этой точки на . Таким образом, точки, соответствующие значениям , расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой , причем аргумент одного из значений равен .

Пример

Решить уравнение .

Решение

Задача равносильна нахождению всех значений корня из комплексного числа. В этом случае .

Определим модуль и аргумент комплексного числа 8i:

Следовательно:

.

Используя формулу извлечения корня, имеем

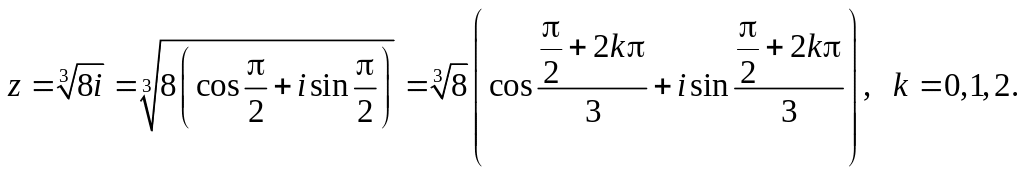
Придавая k последовательно значения от 0 до 2, выписываем решения уравнения:

,

,

.

Для геометрического представления решения уравнения достаточно изобразить одно значение, например (при k=0) – это точка окружности , лежащая на луче . После этого строим правильный треугольник, вписанный в окружность (рис. 3).

у

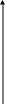
z₁ z₀

2 x

z₂

Рис. 3.