САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СЕРВИСА И ЭКОНОМИКИ

С. Д. Прозоровская, т.И. Филиппова

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

для практических занятий

по теме «КОМПЛЕКСНЫЕ ЧИСЛА»

Санкт – Петербург

2010

Задача 1

Комплексными числами называются всевозможные упорядоченные пары действительных чисел, для которых определены операции сложения и умножения:

;

.

Введенные операции подчиняются законам ассоциативности, коммутативности и дистрибутивности. Число (0;0) назовем нулем. Множество всех комплексных чисел обозначается символом С.

Комплексное число можно записать в следующих формах: алгебраической, тригонометрической и показательной.

Алгебраическая форма комплексного числа

Выражение вида

(1)

где х и у – произвольные действительные числа, i – мнимая единица, удовлетворяющая условию , называется алгебраической формой записи комплексного числа.

Число х называется действительной частью комплексного числа z и обозначается

,

число у называется мнимой частью комплексного числа z и обозначается

.

При число совпадает с вещественным числом х, если число называется чисто мнимым.

На множестве С не определены операции сравнения. Два комплексных числа называются равными, если у них равны соответственно действительные и мнимые части:

.

Комплексные числа называются сопряженными, если у них равны действительные части, а мнимые противоположны по знаку; сопряженные числа обозначают

.

Тригонометрическая форма комплексного числа

Комплексное число изображается на плоскости Оху точкой М с координатами (х;у), либо вектором, начало которого находится в точке О(0;0), а конец – в точке (рис. 1).

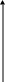у=Im z

М(х,у)

r



0 х=Re z

Рис. 1

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось Ох – действительной осью, ось Оу – мнимой осью.

Число r – длина радиус-вектора точки (расстояние точки М от начала координат) называется модулем комплексного числа

. ( 2 )

Угол , который образован вектором с осью Ох и отсчитываемый от положительного направления оси Ох, называется аргументом комплексного числа и обозначается Arg z.

Аргумент комплексного числа определен с точностью до слагаемого, кратного :

где – главное значение аргумента, определяемое условием

.

Аргумент числа неопределен.

Если вектор расположен в верхней полуплоскости, то угол  отсчитывается от положительного направления оси Ох против часовой стрелки до направления вектора , в данном случае .

Если вектор расположен в нижней полуплоскости, то угол  отсчитывается от положительного направления оси Ох по ходу часовой стрелки до направления вектора , в данном случае .

Если , то будем считать, что .

В результате можно записать:

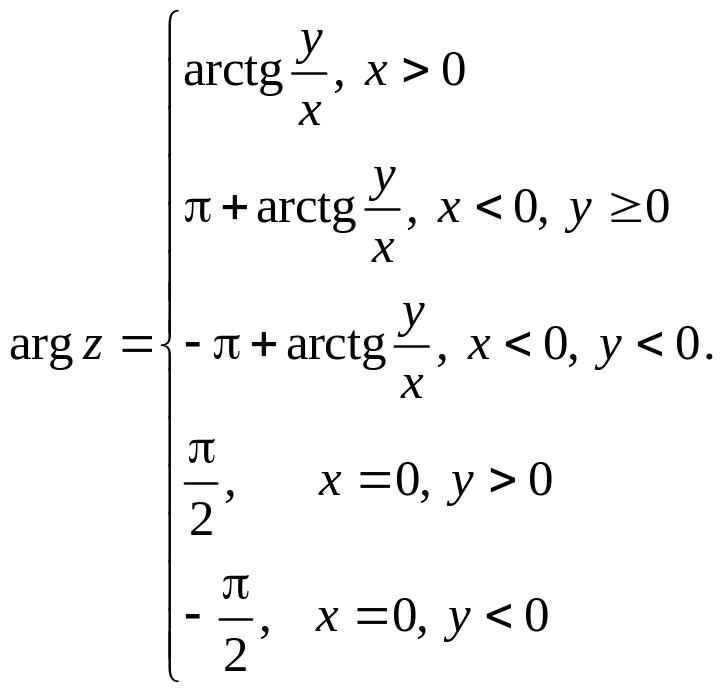(3)

Учитывая, что , получим

.

Запись комплексного числа в виде

( 4 )

называется тригонометрической формой записи комплексного числа.