Структурная модель Нельсона

Структурная модель Нельсона [31], [32].

В качестве показателя надежности принимается вероятность Р(п) безотказного выполнения п прогонов программы. Для j-ro прогона вероятность отказа представляется в виде

где − индикатор отказа на -м наборе данных; − вероятность появления -го набора в -м прогоне. Тогда

Если − время выполнения j-го прогона, то интенсивность отказов

Практическое использование формул (10.54) и (10.55) затруднено из-за множества входов и большого количества трудно оцениваемых параметров модели. На практике надежность программ оценивается по результатам тестовых испытаний, охватывающих относительно небольшую область пространства исходных данных.

Для упрощенной оценки в [33] предлагается формула

где N − число прогонов; n_i − число обнаруженных при прогоне i-го теста ошибок; − индикатор отсутствия ошибок при прогоне i-го теста.

Для уменьшения размерности задачи множество значений входных наборов разбивают на пересекающиеся подмножества , каждому из которых соответствует определенный путь . Если содержит ошибки, то при выполнении теста на поднаборе будет отказ. Тогда вероятность правильного выполнения одного теста

При таком подходе оценка надежности по структурной модели затруднена, так как ошибка в проявляется не при любом наборе из Gj, а только при некоторых. Кроме того, отсутствует методика оценки по результатам испытаний программ.

Структурная модель роста надежности

Структурная модель роста надежности (модель Иыуду) [34].

Модель является развитием модели Нельсона. В ней делают следующие допущения:

• исходные данные входного набора выбираются случайно в соответствии с распределением

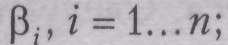
• все элементы программ образуют s классов, вероятность правильного исполнения элемента 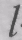-го класса равна

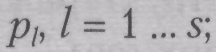
• ошибки в элементах программ независимы. Вероятность правильного исполнения программы по i-му пути

где − количество элементов -го класса в i-м пути. Безусловная вероятность безотказной работы при однократном исполнении программы в период времени до первой обнаруженной ошибки

где п − количество путей исполнения программы.

При корректировании программы после обнаружения ошибки учитывается возможность внесения новой ошибки с помощью коэффициента эффективности корректирования . Вместо в (10.56) следует использовать

где − номер интервала времени между соседними ошибками.

При вероятность не меняется, при вероятность увеличивается, а при , напротив, падает. Для -го интервала вероятность успешного исполнения программы по -му пути

При выражение (10.57) можно представить в виде

Подставляя (10.58) в (10.57), получим:

Если наиболее вероятные пути проверены, то

В формуле (10.59) параметры и можно оценить по экспериментальным данным. Для плана испытаний [NBr], в котором определяются значения − числа прогонов между -м и -м отказами, с помощью метода максимального правдоподобия найдем уравнения относительно искомых оценок:

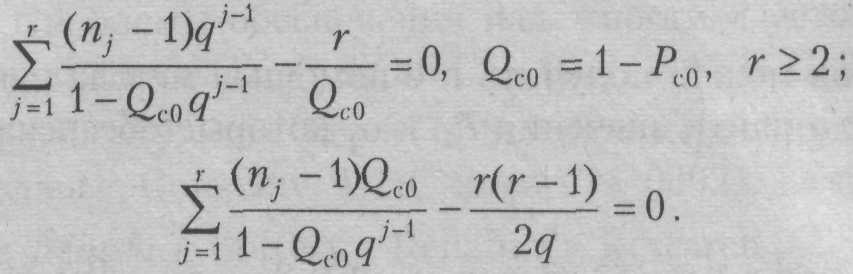
В частности, при r = 2 имеем: