Модель Мусы−Гамильтона
Модель Мусы−Гамильтона [27], [28].
Модель использует так называемую теорию
длительности обработки. Надежность
оценивается в процессе эксплуатации,
в котором выделяют время
реальной работы процессора (наработку)
и календарное время
с учетом простоя и ремонта. Для числа
отказов (обнаруженных ошибок) выводится
формула
где То − наработка между отказами перед началом отладки или эксплуатации;
−
начальное число ошибок;
С − коэффициент пропорциональности.
Из (10.53) находят:
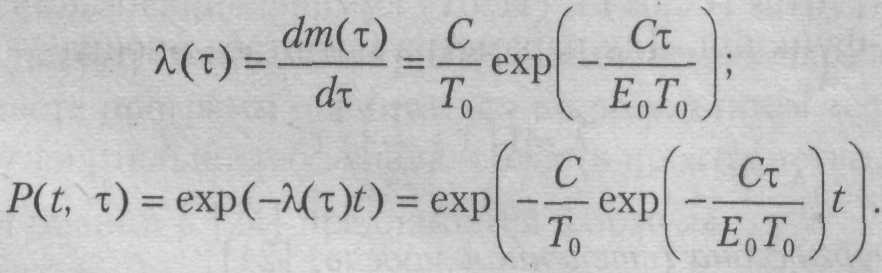
В работе [29] сравниваются экспоненциальная, рэлеевская и смешанная модели. Сравнение проведено на одинаковых наборах данных для предсказания числа ошибок в проекте, состоящем из 4519 небольших программных задач. Результаты предсказания сравниваются с апостериорными данными. Сравнение проводилось и на крупной управляющей программе, содержащей 249 процедур и 115 000 инструкций языка JOVIAL. Было выявлено от 2000 до 4000 ошибок на четырех последовательностях наборов данных. По результатам испытаний определены зависимости числа оставшихся ошибок от времени как для эмпирических данных, так и для предсказанных по рассмотренным моделям. По результатам анализа сделаны следующие выводы:
Экспоненциальная и рэлеевская модели дают более точное предсказание числа ошибок, чем смешанная модель.
Экспоненциальная и рэлеевская модели более пригодны для небольших программ или для небольших длительностей отладки.
Для больших программ или при длительных испытаниях лучшие результаты дают модификации экспоненциальной и рэлеевской моделей.
Геометрическая модель дает удовлетворительные оценки при любой длине программ, но лучше ее использовать для коротких программ и небольшой длительности испытаний.
Экспоненциальная и рэлеевская модели завышают число оставшихся ошибок, а смешанная модель занижает эту величину по сравнению с действительным значением.
Если для большого числа равных интервалов число ошибок на каждом интервале меняется в значительных пределах, то экспоненциальная и рэлеевская модели могут оказаться неудовлетворительными.
Вейбулловская модель (модель Сукерта)
Вейбулловская модель (модель Сукерта) [29].
Модель задается совокупностью соотношений
Достоинство этой модели в том, что она
содержит дополнительный по сравнению
с экспоненциальной моделью параметр
т. Подбирая т и
,
можно получить лучшее соответствие
опытным данным. Значение т подбирают
из диапазона 0<т<1. Оценки параметров
получают с помощью метода моментов. Для
параметра формы значение находят как
решение уравнения
где Г(х) − гамма-функция. Для параметра масштаба оценка
Модель Уолла−Фергюссоиа (степенная модель)
Модель Уолла−Фергюссоиа (степенная модель) [30]
Число обнаруженных и исправленных ошибок определяется с помощью степенной зависимости
где М − степень отлаженности
программ; М0 и
− эмпирические константы.
Отсюда интенсивность отказов
Величина М выражается в человеко-месяцах
испытаний, единицах календарного времени
и т. д. Адекватность модели проверена
на экспериментальных данных, полученных
для систем реального времени и программ
на алгоритмическом языке FORTRAN.
Для грубого предсказания надежности
авторы рекомендуют значение
Во всех рассмотренных моделях программа представлена как «черный ящик», без учета ее внутренней структуры. Кроме того, всюду принято допущение, что при исправлении ошибок новые ошибки не вносятся. Следующие две модели рассматривают программы в виде «белого ящика» − с учетом внутренней структуры. Поэтому они называются структурными.