1. Находим оптимальные размеры и направления грузопотоков по каждому виду груза.
Задача о нахождении оптимальных размеров и направлений грузопотоков решается как транспортная задача линейного программирования. По первому виду груза (картофелю) необходимо представить решение данной задачи вручную методом потенциалов. Для нахождения оптимальных планов грузопотоков других грузов следует использовать средство «Поиск решения» электронной таблицы MS Excel. Методика создания и оптимизации моделей транспортных задач в MS Excel представлена в источниках [1, 2] списка рекомендуемой литературы.
Алгоритм метода потенциалов включает следующие шаги (этапы) расчетов.
Шаг 1. Определение первоначального допустимого (базисного) плана перевозок, затем переходим к выполнению второго шага.
Шаг 2. Анализ распределения и проверка плана перевозок на оптимальность, включающие в себя: 1) расчет потенциалов строк и столбцов; 2) расчет характеристик небазисных переменных. Если все небазисные переменные удовлетворяют условию оптимальности, вычисления заканчиваются, в противном случае переходим к третьему шагу.
Шаг 3. Нахождение нового базисного решения, включающее в себя: 1) определение цепи для клетки, содержащей небазисную переменную, у которой характеристика (по абсолютной величине) наибольшая; 2) определение исключаемой из базиса переменной и перераспределение поставок. Возвращаемся ко второму шагу.
Найдем методом потенциалов оптимальный план грузопотока картофеля для рассматриваемого примера.
Шаг 1. Определение первоначального допустимого (базисного) плана перевозок.
Решение задачи начинается с определения первоначального допустимого плана перевозок при условии, что весь груз от поставщиков должен быть вывезен потребителям, удовлетворив их спрос. Любой план, отвечающий таким требованиям, называется базисным распределением.
В практике решения транспортных задач применяют следующие методы нахождения базисного распределения: метод северо-западного угла, минимального элемента в строке и столбце, наименьшего элемента в матрице, двойного предпочтения и др. При решении транспортной задачи можно пользоваться любым методом нахождения базисного распределения, но от «качества» базисного распределения, т.е. от того, насколько оно близко к оптимальному, зависит количество итераций, необходимых для решения задачи. Поэтому, рекомендуется использовать методы, позволяющие найти лучшее базисное распределение (метод наименьшего элемента в матрице, двойного предпочтения и др.) [4].
Рассмотрим алгоритм
метода
минимального элемента.
На каждом шаге метода
минимального элемента
из всех
не вычеркнутых
клеток транспортной матрицы выбирается
клетка с минимальной стоимостью перевозки
(или расстоянием перевозки)
и в соответствующую клетку заносится
максимально возможная поставка. Если
транспортная таблица имеет несколько
клеток с одинаковыми по величине
минимальными показателями
,
то поставку можно произвести в любую
клетку. Далее вычеркивается соответствующий
столбец или строка и соответствующим
образом корректируются значения спроса
и предложения. Если одновременно
выполняются ограничения и по спросу, и
по предложению, вычеркиваются или
строка, или столбец. Затем просматриваются
невычеркнутые клетки, и выбирается
новая клетка с минимальным показателем
.
Описанный процесс продолжается до тех
пор, пока не останется лишь одна
невычеркнутая строка или столбец.
Представленное ниже базисное распределение грузопотока картофеля найдено методом наименьшего элемента в матрице (табл. 2 – табл. 8).
Таблица 2
Составление базисного плана перевозок товара между складами методом наименьшего элемента в матрице (Итерация 1)
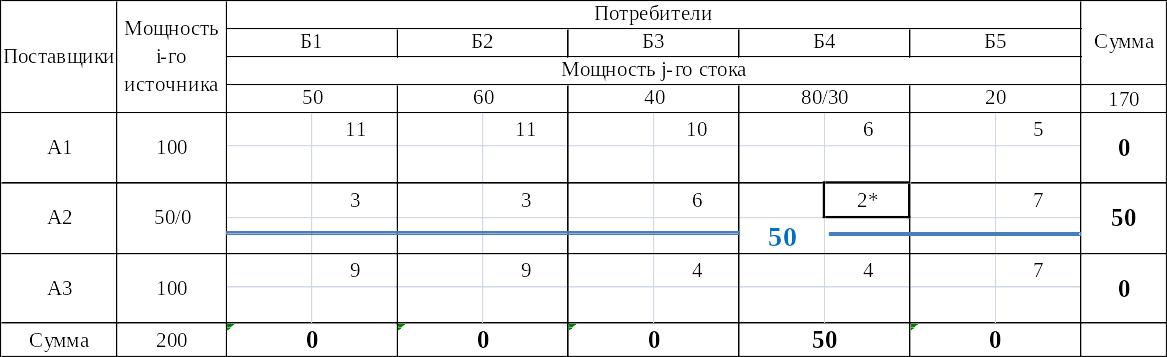
Таблица 3
Составление базисного плана перевозок товара между складами методом наименьшего элемента в матрице (Итерация 2)
Таблица 4
Составление базисного плана перевозок товара между складами методом наименьшего элемента в матрице (Итерация 3)
Таблица 5
Составление базисного плана перевозок товара между складами методом наименьшего элемента в матрице (Итерация 4)
Таблица 6
Составление базисного плана перевозок товара между складами методом наименьшего элемента в матрице (Итерация 5)
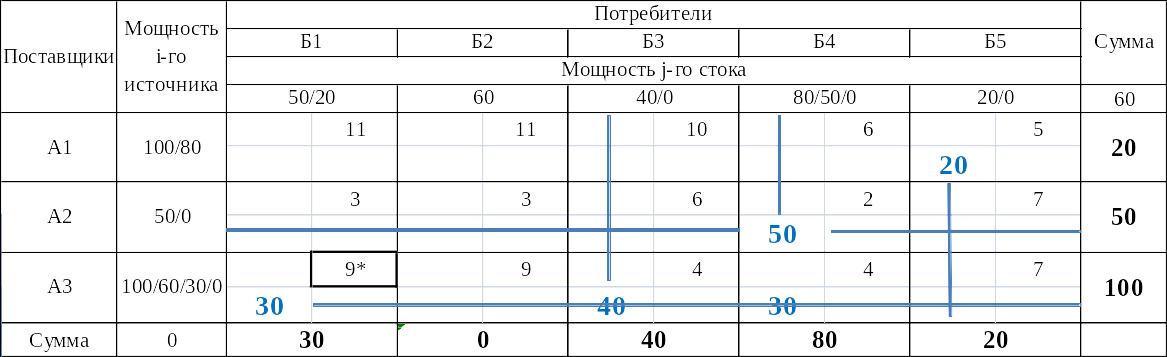
Таблица 7
Составление базисного плана перевозок товара между складами методом наименьшего элемента в матрице (Итерация 6)
Таблица 8
Составление базисного плана перевозок товара между складами методом наименьшего элемента в матрице (Итерация 7)
Значение целевой функции полученного распределения, т.е. транспортная работа составляет
Шаг 2. Анализ распределения и проверка плана перевозок на оптимальность.
Нахождение оптимального плана начинается с анализа первоначального распределения с целью выяснения при помощи потенциалов возможности его улучшения.
Если обозначить потенциалы строк через ui, потенциалы столбцов через vj, показатели критерия оптимальности в занятых клетках через , то уравнение потенциалов можно записать в виде:
,
откуда следует, что
и
.
Используя представленные выше уравнения, находим потенциалы строк и столбцов в распределении, представленные в табл. 9.
Таблица 9
Проверка плана перевозок товара между складами
на оптимальность (расчет потенциалов)
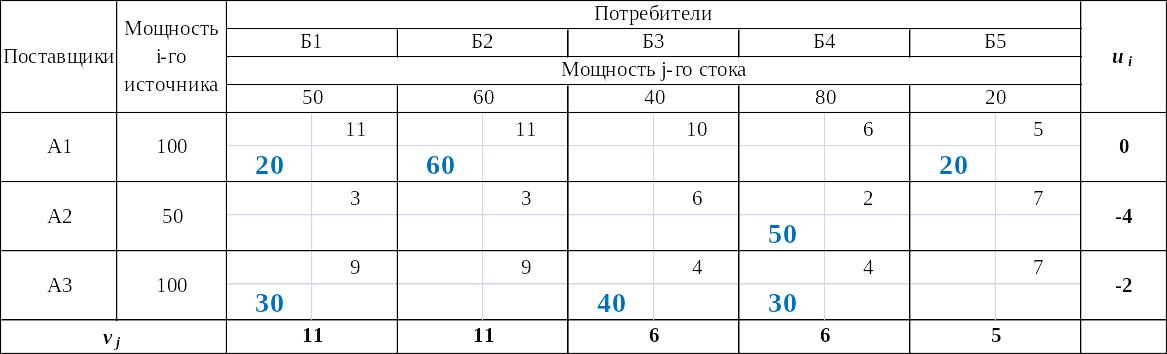
Уравнения потенциалов имеют вид:
Полученная система
имеет 7 уравнений и 8 неизвестных,
следовательно, она неопределенная.
Обычно для решения системы принимают
потенциал первой строки равным нулю
или любому другому числу. В данном случае
потенциал
.
Решая систему, получаем:
.
Характеристики незанятых клеток вычисляют по формуле
.
Если вычисленная
оценка для незанятой клетки будет
отрицательной, то перераспределение
поставок по цепи к этой клетке уменьшает
значение целевой функции (в расчете на
единицу перераспределяемой продукции)
на величину характеристики
.
Если характеристика
равна нулю, то перераспределение к этой
клетке не изменит значение целевой
функции.
Результат расчета характеристик незанятых клеток в рассматриваемом распределении представлен в табл. 10.
Таблица 10
Проверка плана перевозок товара между складами
на оптимальность (расчет характеристик незанятых клеток)
Характеристики незанятых клеток следующие:
А1Б3: 10 – (0 + 4) = 6; А1Б4: 6 – (0 + 6) = 0;
А2Б1: 3 – (–4 + 11) = –4; А2Б2: 3 – (–4 + 11) = –4;
А3Б3: 6 – (–4 + 6) = 4; А2Б5: 7 – (–4 + 5) = 6;
А3Б2: 9 – (–2 + 11) = 0; А3Б5: 7 – (–2 + 5) = 4.
В рассматриваемом распределении имеются незанятые клетки с отрицательными характеристиками, следовательно, план является неоптимальным и требуется нахождение нового базисного решения.
Шаг 3. Нахождение нового базисного решения.
Если получены несколько отрицательных характеристик, то перераспределение делают для той клетки, у которой оценка (по абсолютной величине) наибольшая. В данном случае, поскольку имеются две одинаковые отрицательные оценки в клетках А2Б2 и А2Б3, выбор клетки произвольный.
Для всех цепей в транспортной задаче, решаемой методом потенциалов, характерны следующие особенности: цепь является обязательно замкнутым многоугольником; вершинами цепи являются занятые клетки, за исключением одной, для которой делается перераспределение поставок; все углы цепи прямые и каждая сторона цепи принадлежит к одному столбцу или к одной строке; отрезки цепи могут проходить через занятые клетки, не являющиеся вершинами данной цепи. При расстановке знаков в цепи вершина клетки, для которой определяется поставка, получает всегда положительный знак, а у остальных вершин цепи знаки чередуются.
Для перераспределения поставки выберем одну из двух клеток с наименьшей отрицательной характеристикой, например клетку А2Б1. Цепь, построенная для данной клетки, представлена в табл. 11.
Таблица 11
Нахождение нового плана (формирование цепи для клетки с отрицательной характеристикой)
Для определения поставки в незанятую вершину поступают следующим образом. В вершинах цепи отыскивают наименьшую (по абсолютной величине) отрицательную поставку, на которую уменьшают все поставки с отрицательным знаком и увеличивают поставки с положительным знаком. В рассматриваемой цепи наименьшая по абсолютной величине отрицательная поставка содержится в клетке А3Б1, следовательно, незанятая клетка получит 30 т.
Новый план перевозок товара между складами после перераспределения поставок представлен в табл. 12.
Таблица 12
Нахождение нового плана (перераспределение поставок)
Значение целевой функции полученного распределения, т.е. транспортная работа составляет
Таким образом, первоначальное базисное распределение удалось улучшить на 1630 – 1510 = 120 ткм.
Затем необходимо возвратится к шагу 2 и проверить новый базисный план перевозок на оптимальность.
Шаг 2. Анализ распределения и проверка плана перевозок на оптимальность.
В табл. 13 и табл. 14 представлены результаты проверки нового плана перевозок на оптимальность.
Таблица 13
Проверка нового плана перевозок товара между складами
на оптимальность (расчет потенциалов)
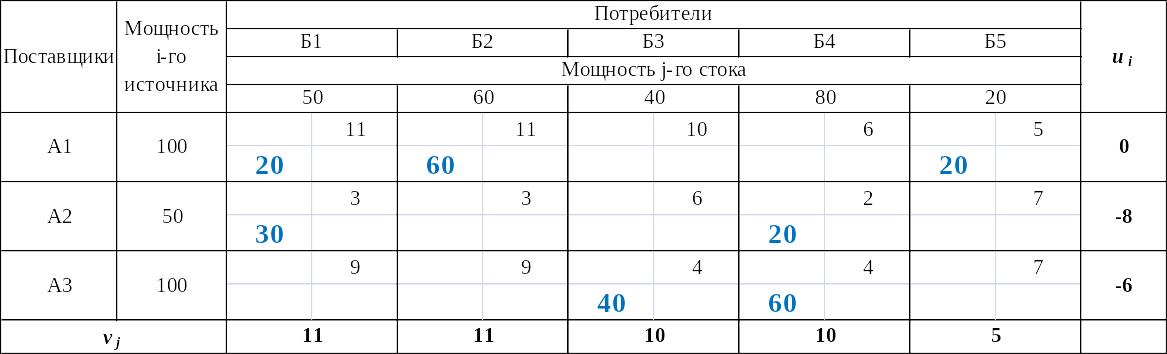
Таблица 14
Проверка нового плана перевозок товара между складами
на оптимальность (расчет характеристик незанятых клеток)
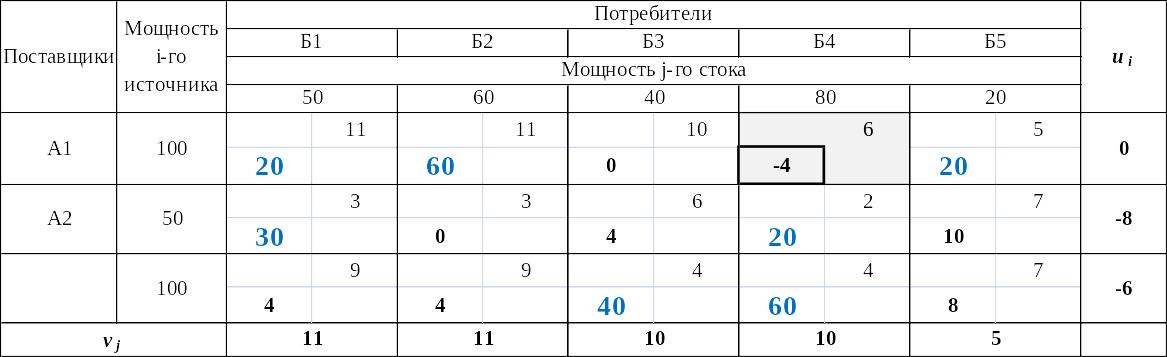
В рассматриваемом распределении имеется одна незанятая клетка с отрицательной характеристикой – А1Б4, следовательно, план является неоптимальным и требуется нахождение нового базисного решения.
Шаг 3. Нахождение нового базисного решения.
Формирование цепи для клетки с отрицательной характеристикой представлено в табл. 15, а перераспределение поставок представлено в табл. 16.
Таблица 15
Нахождение нового плана (формирование цепи для клетки с отрицательной характеристикой)
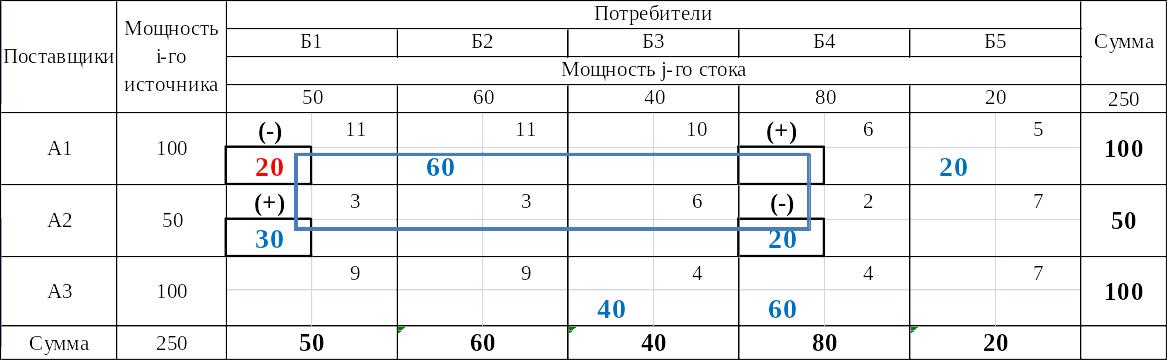
Таблица 16
Нахождение нового плана (перераспределение поставок)
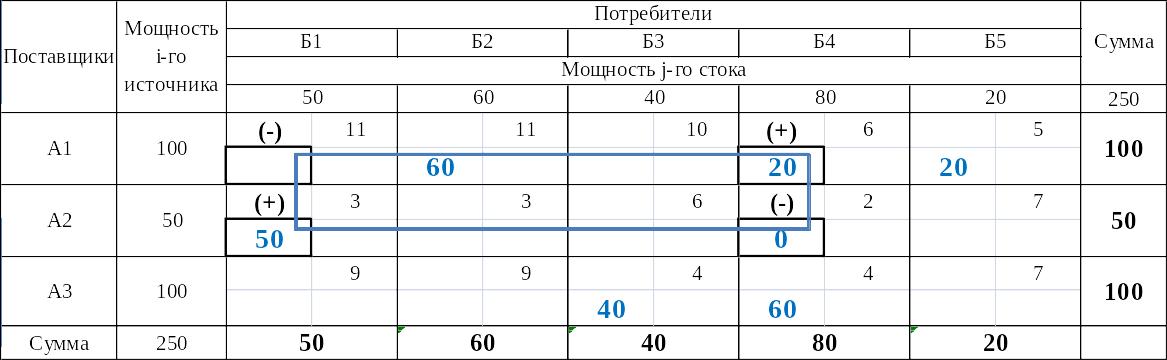
Значение целевой функции полученного распределения, т.е. транспортная работа составляет
Таким образом, предыдущее базисное распределение удалось улучшить на 1510 – 1430 = 80 ткм, а первоначальное – на 1630 – 1430 = 200 ткм.
Шаг 2. Анализ распределения и проверка плана перевозок на оптимальность.
В табл. 17 и табл. 18 представлены результаты проверки нового плана перевозок на оптимальность.
Таблица 17
Проверка нового плана перевозок товара между складами
на оптимальность (расчет потенциалов)
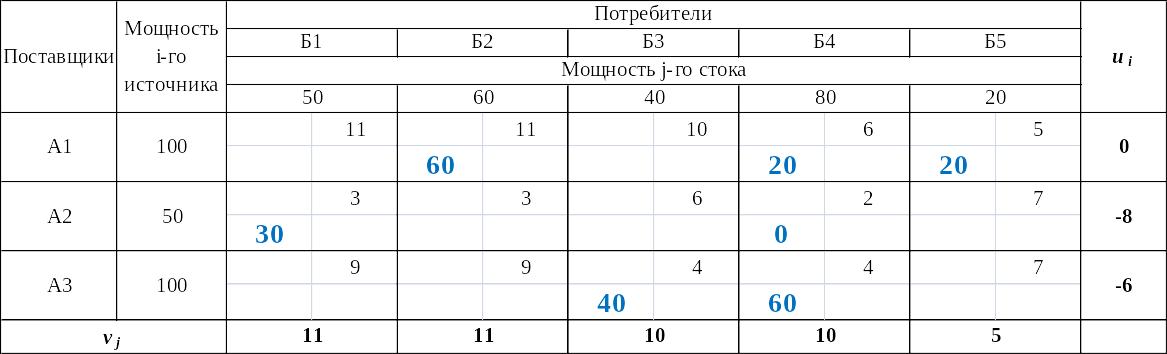
Таблица 18
Проверка нового плана перевозок товара между складами
на оптимальность (расчет характеристик незанятых клеток)
Характеристики всех незанятых клеток Eij ≥ 0, следовательно, план перевозок является оптимальным.
Проверку правильности полученного решения необходимо сделать, решив ту же задачу с помощью средства «Поиск решения» электронной таблицы MS Excel. В табл. 19 представлено полученное решение.
Таблица 19
Оптимальный план грузопотока картофеля
Поставщики |
Потребители |
Предложение, т |
||||
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
||
А1 |
11 |
11 |
10 |
6 |
5 |
100 |
0 |
60 |
0 |
20 |
20 |
||
А2 |
3 |
3 |
6 |
2 |
7 |
50 |
50 |
0 |
0 |
0 |
0 |
||
А3 |
9 |
9 |
4 |
4 |
7 |
100 |
0 |
0 |
40 |
60 |
0 |
||
Спрос, т |
50 |
60 |
40 |
80 |
20 |
|
Сравнение решений, представленных в табл. 16 и табл. 19, показывает, что решения совпадают, следовательно, решение данной задачи вручную методом потенциалов является верным.
В табл. 20 представлен оптимальный план грузопотока репчатого лука, а в табл. 21 – оптимальный план грузопотока капусты.
Таблица 20
Оптимальный план грузопотока репчатого лука
Поставщики |
Потребители |
Предложение, т |
||||
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
||
А1 |
11 |
11 |
10 |
6 |
5 |
20 |
0 |
0 |
0 |
0 |
20 |
||
А2 |
3 |
3 |
6 |
2 |
7 |
100 |
20 |
30 |
25 |
25 |
0 |
||
А3 |
9 |
9 |
4 |
4 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
||
Спрос, т |
20 |
30 |
25 |
25 |
20 |
|
Таблица 21
Оптимальный план грузопотока капусты
Поставщики |
Потребители |
Предложение, т |
||||
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
||
А1 |
11 |
11 |
10 |
6 |
5 |
50 |
30 |
0 |
0 |
20 |
20 |
||
А2 |
3 |
3 |
6 |
2 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
||
А3 |
9 |
9 |
4 |
4 |
7 |
150 |
20 |
40 |
70 |
20 |
0 |
||
Спрос, т |
50 |
40 |
70 |
20 |
20 |
|
Примечание. Оптимальные планы грузопотоков, представленные в табл. 20, табл. 21 и табл. 23, найдены с помощью средства «Поиск решения» электронной таблицы MS Excel.