Лабораторная работа № 7 Проверка теорем о взаимности работ и перемещений

Цель работы: экспериментальная проверка теорем о взаимности работ перемещений.

Общие сведения

Рассмотрим шарнирно опертую балку (рис. 1), выделим два сечения балки I и II, отстоящие на одинаковых расстояниях от опор.

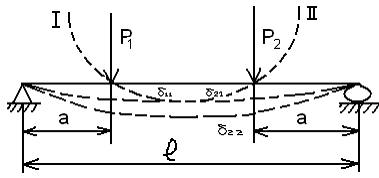
Рис. 1.

В общем случае можно рассматривать сечения, отстоящие на разных расстояниях от опор балки. Приложим силу , в сечении I. При этом балка прогибается, сечение I получит перемещение , а сечение II – перемещение . Если теперь приложить силу в сечении II, то сечение I получит дополнительное перемещение , а в сечение II – . Между силами - и вызываемыми ими перемещениями и сечений I- II балки существует зависимость, которая формулируется теоремой о взаимности работ.

Теорема о взаимности работ (теорема Бетти)

Работа силы на перемещение точки ее приложения, вызванном равна работе силы на перемещение точки ее приложения, вызванном силой : = . Частным случаем теоремы о взаимности работ при = является теорема о взаимности перемещений.

Теорема о взаимности перемещений (теорема Максвелла)

Перемещение точки приложения первой силы, происходящее под действием второй силы, равно перемещению точки приложения второй силы, вызванному действием первой силы : = .

Описание испытательной установки

Для проведения работы используется испытательная установка (рис.2). Установка состоит из исследуемой балки 1, основания 2, подвижной 3 и неподвижной 4 опор, двух индикаторных стоек 5 и двух гиревых подвесов 6. Балка изготовлена из стальной полосы (E = 2 кг/см²) прямоугольного поперечного сечения (шириной В = 40 мм, высотой Н = 7 мм ) и установлена на шарнирных опорах, длина пролета = 1000 мм.

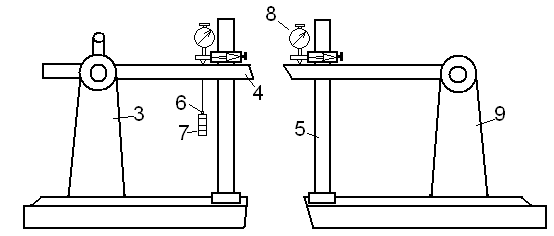
Рис. 2.

Нагружение балки осуществляется с помощью гиревых подвесов (вес каждого подвеса G = 0,5 кг) и набора грузов 7. Нагрузку прикладывают сосредоточенно в сечениях балки 1 и 2, отстоящих на одинаковых расстояниях (а = 200 мм) от обеих опор балки. В этих сечениях определяются прогибы при помощи двух индикаторов часового типа 8 с ценой деления 0,01 мм.

Порядок проведения работы

1. Снять гиревые подвесы и установить призы для гиревых подвесов в сечениях 1 и 2 балки на расстоянии а = 200 мм. От обеих опор ( отметки 20 и 80 на шкале балки ).

2. Установить большие стрелки обоих индикаторов на “ 0 “ и записать показания и в соответствующих графах табл. 1 при нулевой нагрузке.

3. Установить гиревой подвес в сечении 1 и нагрузить балку в этом сечении нагрузкой = 2,5 кг (с учетом веса гиревого подвеса ) (рис. 3).

Записать показания индикатора в сечении 2 .Разгрузить балку, снять гиревой подвес

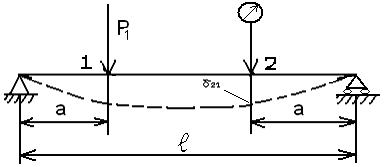
Рис. 3.

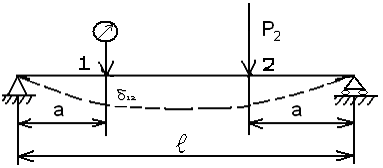
Рис. 4.

4. Установить гиревой подвес в сечении 2 и нагрузить балку в этом сечении нагрузкой Р₂ = 3,5 кг (с учетом веса гиревого подвеса (рис. 4)). Записать показание Т индикатора в сечении 1. Разгрузить балку, снять гиревой подвес.

5. Повторить опыт дважды, записывая соответствующие данные в табл. 1.

6. Определить прогибы балки в сечениях 1 и 2, вычисляя разность показаний индикаторов для каждого нагружения:

∆T₁ = δ₁₂ ,

∆T₂ = δ₂₁ .

7. Вычислить работу силы Р₁ на перемещении сечения 1 – δ₁₂, вызванном силой Р₂ :

А₁ = Р₁δ₁₂

и работу силы Р₂ на перемещении сечения 2 – δ₂₁ , вызванном силой Р₁ :

А₂ = Р₂δ₂₁ .

Результаты записать в табл. 1.

8. Проверить справедливость теоремы о взаимности работ, т.е. выполнение равенства, вычисляя расхождение:

.

Результаты измерений занести в табл. 1.

9. Повторить опыт, прикладывая в сечениях 1 и 2 балки разные нагрузки Р₁ = Р₂, и записывая соответствующие показания в табл. 2.

10. Определить прогибы балки в сечениях 1 и 2, вычисляя разности показаний индикатора для каждого нагружения:

∆T₁ = δ₁₂ ,

∆T₂ = δ₂₁ .

11. Проверить справедливость теоремы о взаимности перемещений, т.е. выполнение равенства, вычисляя расхождение:

.

Результаты вычислений занести в табл. 2.

Оформить отчет по прилагаемой форме.