Лабораторная работа 3 Определение упругих постоянных материала

Общие сведения. При деформации материалов в упругой стадии имеет место прямопропорциональная зависимость между линейной деформацией и нагрузкой. Впервые эта закономерность была замечена Робертом Гуком (1660), поэтому получила название закона Гука:

,

где - абсолютная линейная деформация,

Р – продольная нагрузка,

– длина образца ,

F – поперечное сечение,

Е –величина, зависящая только от материала и называемая модулем упругости (модулем Юнга).

Так как – относительная деформация, а – напряжение, то закон Гука можно преобразовать в следующий вид:

.

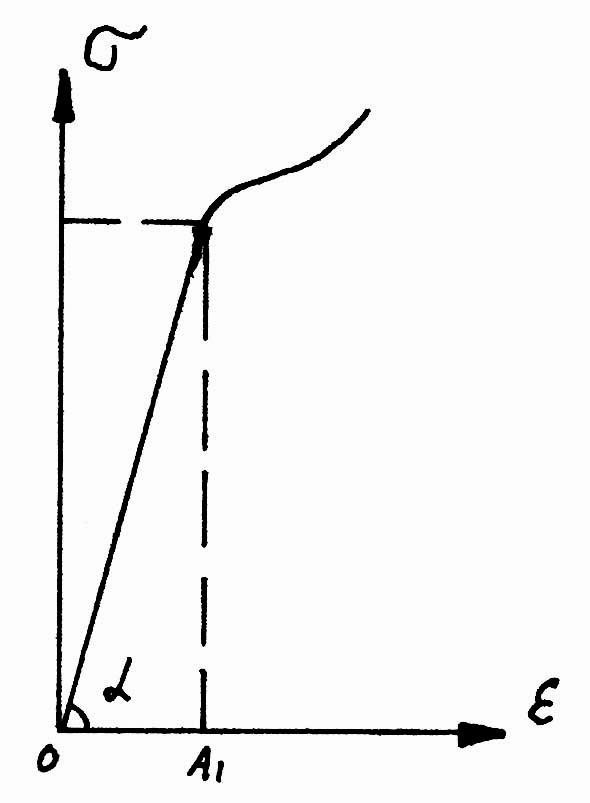
На диаграмме напряжения модуль упругости представлен тангенсом угла наклона прямой

.

Чем больше , тем больше деформация при тех же напряжениях, тем более жестким будет материал. Таким образом, модуль упругости Е характеризует жесткость при растяжении. Размерность модуля упругости выражается в паскалях: Па = Н/м² .

Одновременно с продольной деформацией бруса происходит изменение его поперечных размеров. Связь между поперечной и продольной деформацией определяется коэффициентом поперечной деформации .

Величина коэффициента поперечной деформации (коэффициент Пуассона) никогда не превышает 0,5 и зависит только от материала. Следовательно, для данного материала коэффициент поперечной деформации – величина постоянная.

Цель работы. Определение модуля упругости Е, определение величины коэффициента Пуассона (μ). Т. е., отношение относительной поперечной деформации (Е₁) при растяжении (сжатии) к относительной продольной деформации (Е), найденным в пределах пропорциональности. Коэффициент поперечной деформации μ, так же как и модуль упругости Е, является характеристикой упругих свойств материалов. Для материалов, упругие свойства которых одинаковы во всех направлениях, упругие постоянные Е и μ полностью характеризуют эти свойства. Такие материалы называют изотропными. К ним относят сталь и другие металлы, большинство естественных камней, бетон, каучук, неслоистые пластмассы.

Для определения коэффициента поперечной деформации необходимо подвергнуть образец растяжению либо сжатию с одновременным измерением продольных и поперечных деформаций. Так как напряжения в процессе испытания не должны превосходить предел пропорциональности, мы будем иметь дело с весьма малыми упругими деформациями. Для измерения малых деформаций применяют специальные тензометры. На рис. стр. 23 показан рычажно-винтовой тензометр конструкции проф. Аистова Н.Н. Частью, воспринимающей деформацию, является рама прибора 8 вместе с призмой 1, прижимаемая струбциной к испытываемому образцу АВ. Расстояние между острием ножа 2 опоры прибора и нижним ребром призмы 1 является базой прибора S . При изменении этого расстояния на величину S призма 1 повернётся вокруг верхнего ребра на некоторый угол, повернётся вместе с призмой 1 перо 3, скреплённое с призмой жёстко. Верхний конец пера переместится на величину .

Коэффициент увеличения в приборе равен 5.

Величина замеряется микрометрическим винтом 4, помещенным в корпусе прибора, где имеется отверстие с резьбой. Шаг нарезки винта (т.е. перемещение его вдоль оси при одном обороте t = 0,5 мм). На микрометрическом винте насажен круглый диск 5, на котором нанесена круговая шкала, имеющая 100 делений. Отсчёт по шкале проводится по указателю 6, скреплённому с корпусом прибора, изменение отсчёта по шкале на величину соответствует перемещению винта 4 на

мм .

Определение деформации во время отсчёта по шкале проводится при соприкосновении острия винта 4 с пером 3, что фиксируется при помощи электрического звонка, так как к стержню 3 и винту 4 подключены контакты электрической цепи, а верхняя часть прибора изолирована от нижней посредством прокладки 7.

В момент отсчёта равно перемещению пера 3.

Коэффициент прибора 200 = 1000.

Таким образом, каждому делению шкалы на диске 5 соответствует изменение базы на один микрон.

Рычажный тензометр обычно имеет базу 20 мм, но при помощи специальных удлинителей база может быть увеличена до любой величины в пределах 50 – 100 мм. Прибор прижимается к испытываемому телу АВ при помощи струбцинки. Жёсткая рамка прибора 6 вместе с призмой 1 составляет часть прибора, воспринимающую деформацию, происходящую на участке между призмой 1 и ножом 2 (на базе S).

Частью прибора, увеличивающей деформацию, является рычаг 3 жестко соединенный с призмой 1 и стрелка 5, шарнирно соединенная с рычагом 3 тягой 4.

Стрелка 5 верхним концом 8 шарнирно прикреплена к раме. По шкале 7 проводятся отсчеты. При увеличении длины S (зафиксированной базой прибора) на величину произойдет поворот призмы 1 вокруг её верхнего ребра на некоторый угол. Вместе с призмой на тот же угол повернется рычаг 3 и при помощи тяги 4 отклонит стрелку. Вследствие поворота стрелки 5 нижний конец её переместится по шкале 7 на величину пропорционально удлинению . Коэффициент увеличения зависит от соотношения плеч рычагов 3 и 5 и равен R = = .

Обычно увеличение прибора R равно 1000. Для повышения точности отсчетов шкала 7 снабжена прорезью с зеркалом. При отсчете нужно располагать глаз на уровне стрелки.

При опыте тензометры устанавливают на тонкой и широкой пластинке ( см. рис. 3), при этом два из них (1 и 2) закреплены на образце вдоль его длины, а 3 – поперёк.

ПРОВЕДЕНИЕ ОПЫТА

После обмера пластины её закрепляют в захватах разрывной машины. Прежде чем приступить к нагружению образца, необходимо определить величину наибольшей силы, которую можно приложить к образцу, не вызывая в материале напряжений, превосходящих его предел пропорциональности:

,

для стали предел пропорциональности может быть взят =200 МПа.

Для обжатия образца в захватах дают небольшую предварительную нагрузку /порядка 5000 н – (500 кг); при этой нагрузке проводят первые отсчёты по проборам и записывают их в журнал наблюдений (см. протокол опыта), для последующего вычисления продольных и поперечных деформаций пластины. Затем, последовательно увеличивая напряжения в материале ступенями порядка 20+30 МПа, проводят отсчёты при каждой ступени нагружения образца. По окончании опыта рекомендуется разгрузить образец до начальной нагрузки и сделать контрольные отсчёты по приборам. Поскольку образец подвергался растяжению в пределах упругости, контрольные отсчёты должны совпадать с первоначальными.

ОБРАБОТКА ДАННЫХ ОПЫТА

При вычислении значения модуля продольной упругости Е следует использовать закон ГУКА: , откуда .

Для избежания влияния возможных погрешностей в показаниях приборов подсчет лучше вести по среднему приращению показаний приборов, поэтому следует предварительно подсчитать:

1. Среднее приращение нагрузки 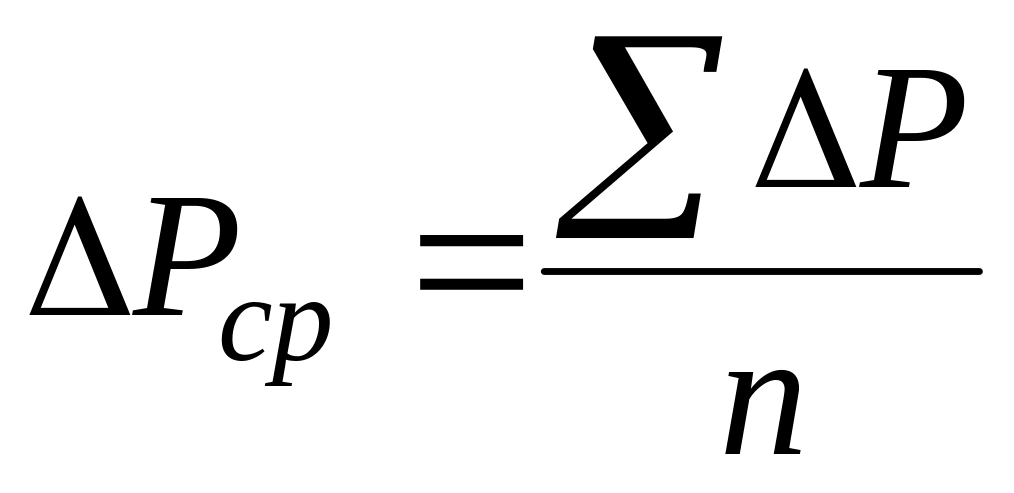, где n – число приращений.

2. Среднее приращение продольной деформации , где ∑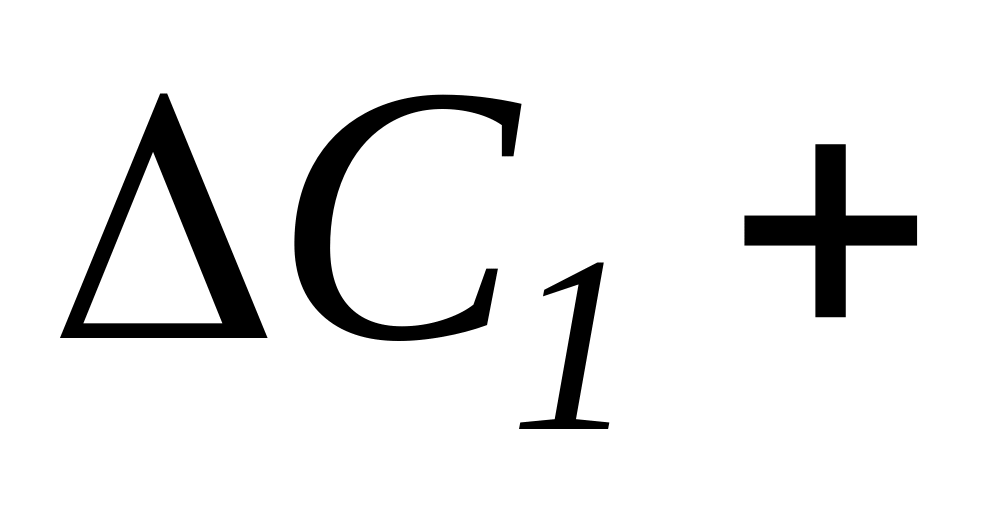 ∑ 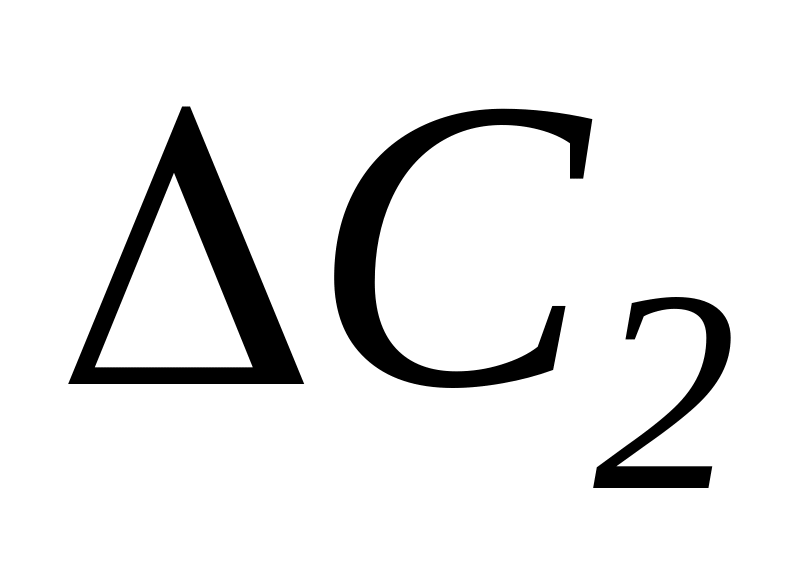– сумма приращений показаний продольных тензометров в делениях, а l – коэффициент увеличения тензометров.

3. Среднее приращение поперечной деформации .

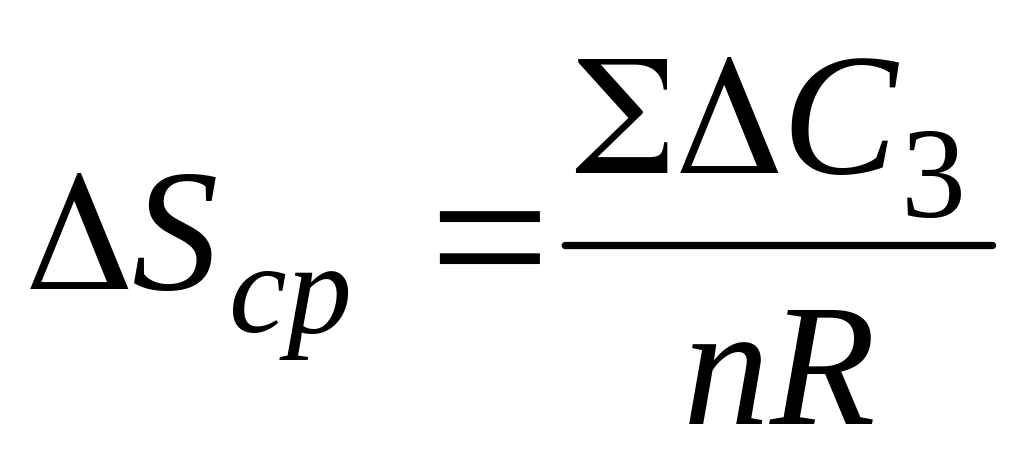4. относительную продольную деформацию .

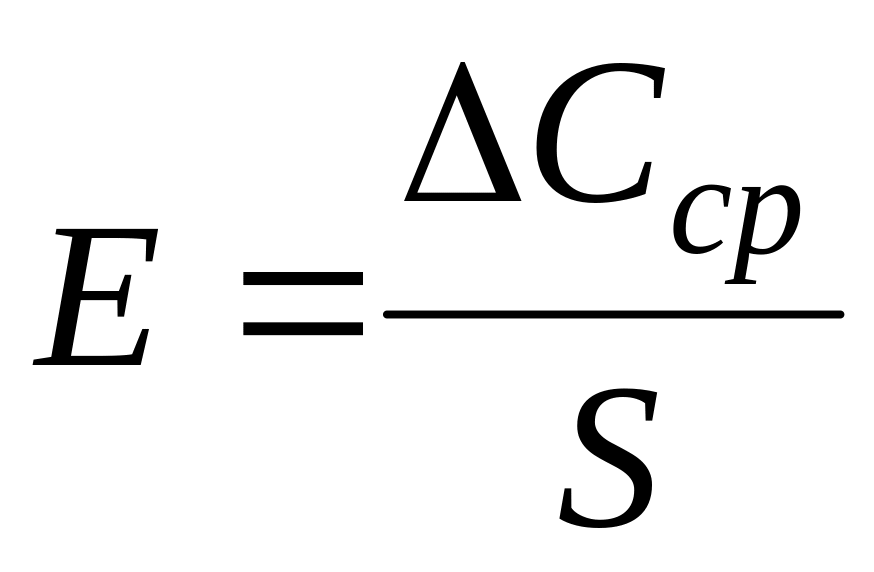5. Относительную поперечную деформацию .

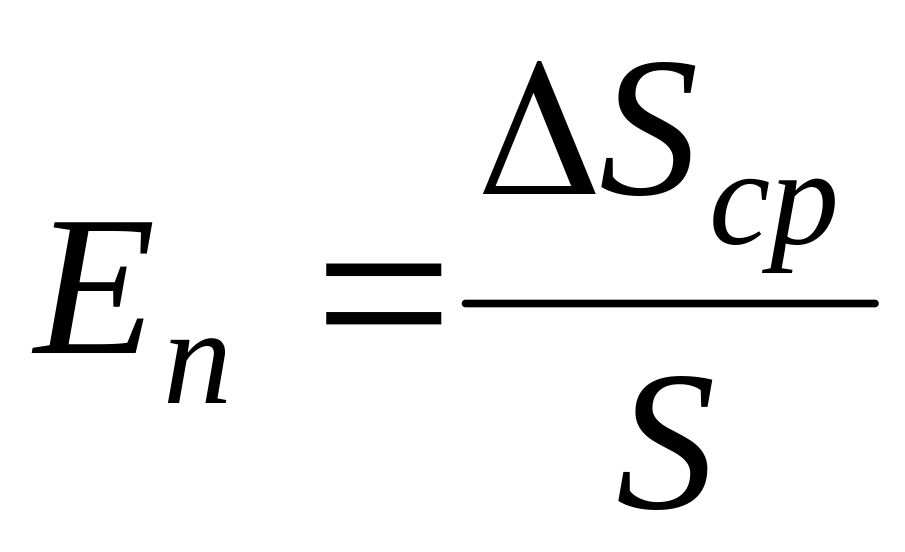6. Затем подсчитываем модуль упругости Е по формуле 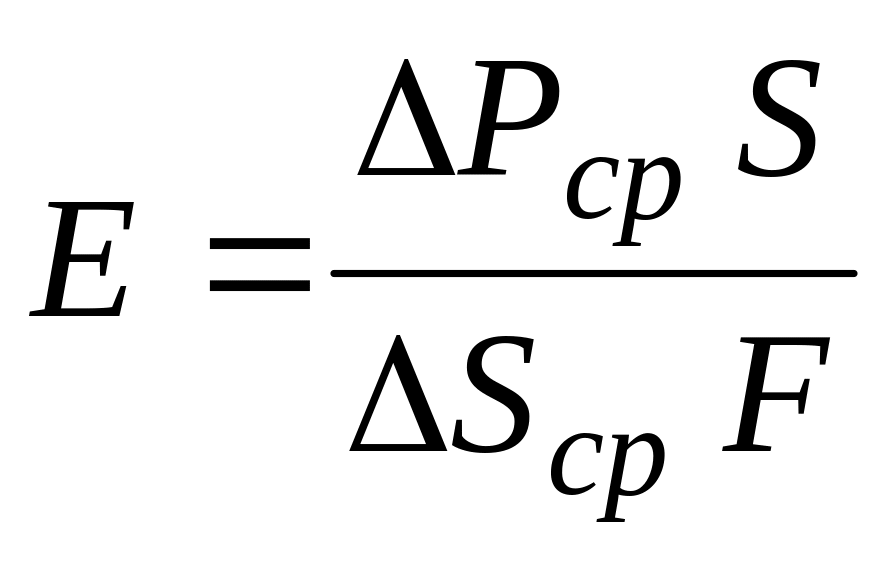и коэффициент поперечной деформации .

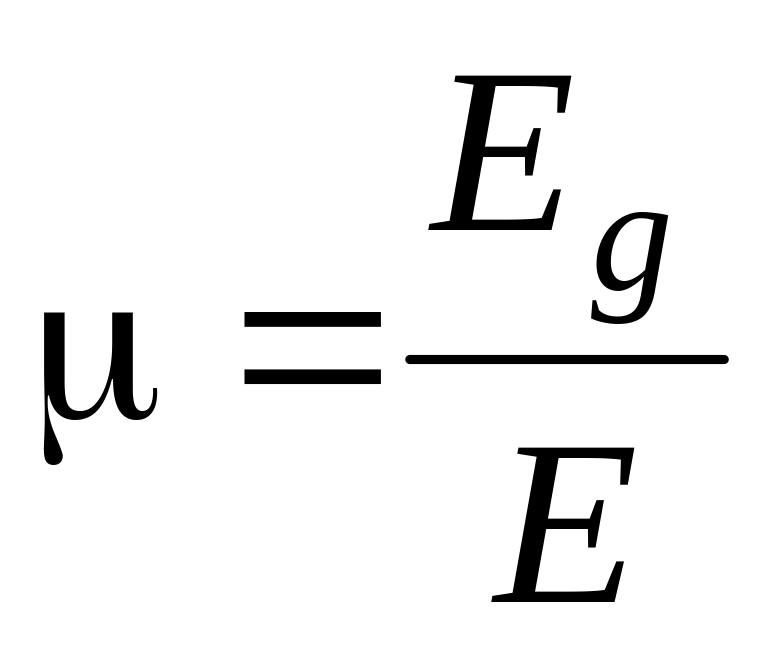В завершении работы вычерчивается график, иллюстрирующий закон Гука. По оси ординат откладывается напряжение в МПа или кг/см², а по оси абсцисс – относительное удлинение в %. Наносят точки, соответствующие каждой ступени нагружения образца с координатами, а затем проводят среднюю прямую. Попадание точек на прямую или незначительное их отклонение от прямой явится подтверждением закона Гука для испытуемого материала.

ОТЧЁТ О ПРОДЕЛАННОЙ РАБОТЕ

Определение упругих постоянных материала.

Цель работы: определить коэффициент поперечной деформации μ (коэффициент Пуассона), модуль продольной упругости Е из опыта на растяжение. Испытания проводятся на разравной машине.

Для измерения деформации использованы тензометры Аистова.

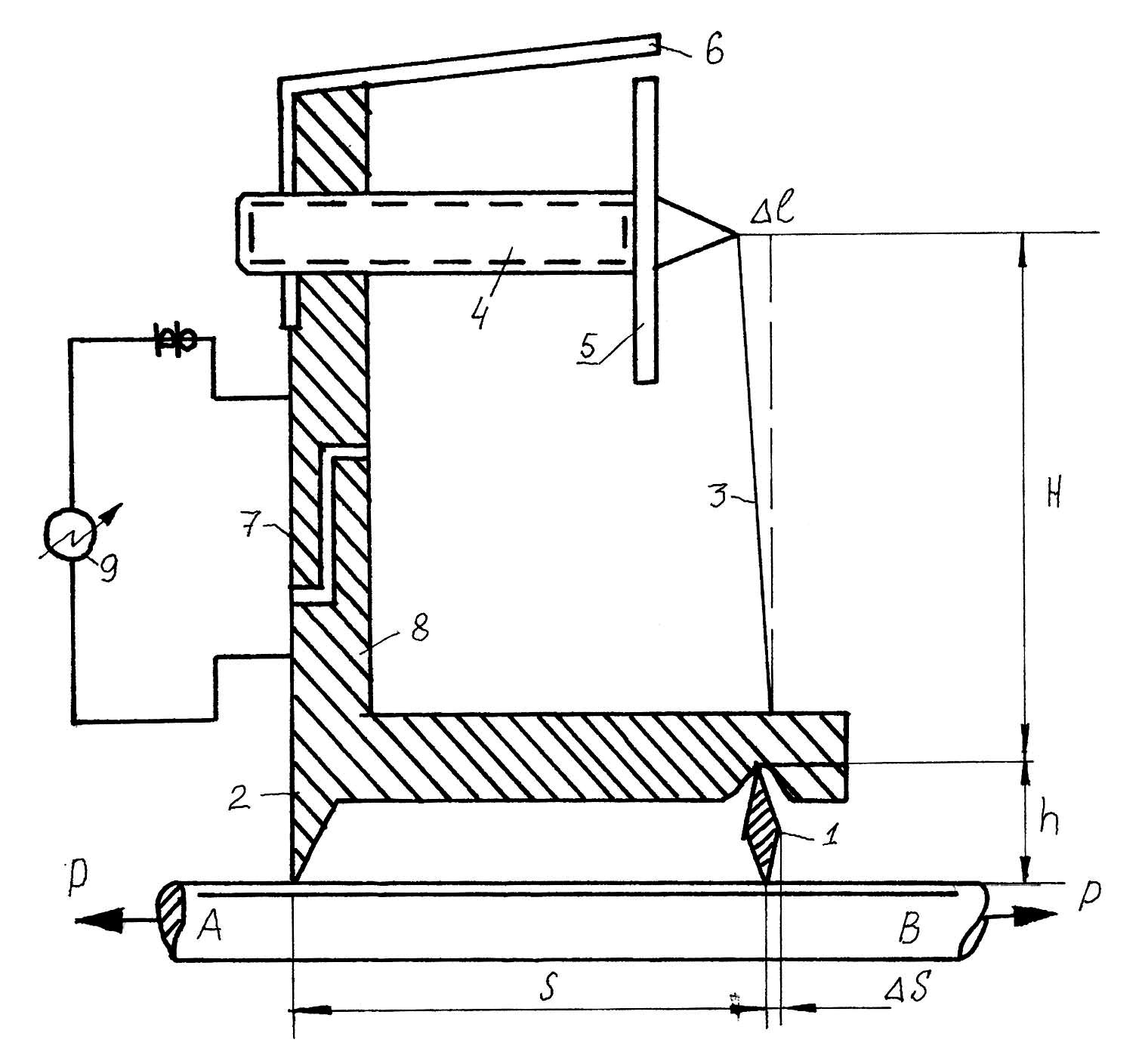
Рычажно-винтовой тензометр конструкции проф. Аистова Н.Н.

1 – призма, 2 – нож опоры, 3 – стержень, 4 – винт, 5 – диск с делениями, 6 – указатель, 7 – изоляция, 8 – основание прибора, 9 – электрический звонок. S – база замера, АВ – образец.

Размеры образца Схема установки образца

при испытании

= см

b = cм

F = см²(м²)

Предельная нагрузка

P_max < σ_пц F =

σ_пц = МПа (кг/см²)

Таблица 1

Результаты наблюдений

Наг­рузка Р, кг	Продольные тензометры					Поперечные тензометры

Среднее приращение нагрузки: .

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:

1. Что такое модуль упругости?

2. Какие свойства материала характеризует модуль упругости?

3. Какую размерность имеет модуль упругости?

4. Дайте определение коэффициента Пуассона и как он определяется ?

5. Сформулируйте закон Гука для линейных деформаций.

6. Что такое абсолютная и относительная продольная и поперечная деформации?

7. Что происходит с поперечными размерами бруса при сжатии?

8. Как устроен прибор для малых деформаций бруса (тензометр)?

9. Что такое коэффициент увеличения тензометра?

10. Как опытным путем определить модуль упругости?

11. В каких пределах может находиться величина коэффициента Пуассона?

ЛИТЕРАТУРА

4. Беляев Н. М. Сопротивление материалов.

5. Дарков А. Б. Сопротивление материалов.

6. Афанасьев А. М. Лабораторный практикум по сопротивлению материалов.