Лекция 3. Числовые характеристики дискретной и непрерывной случайной величины

Цель лекции: Изучить основные числовые характеристики дискретной и непрерывной случайной величины, дать определения и понятие о двумерной и многомерной плотности вероятностей.

• ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Основные понятия и термины.

1. Математическое ожидание дискретной с.в.

2. Центр распределения вероятностей с.в.

3. Центрированная с.в. ξ - m _ξ или отражение

4. Дисперсия

1.1. Математическое ожидание

Пусть имеем дискретную случайную величину ξ с соответствующим законом распределения

ξ Х₁ Х₂ Х₃ … Х_{R …} Х _n

Р_(ξ) = Х_R Р₁ Р₂ Р₃ Р_R Р _n

Очевидно в определенном случае эти вероятности не равны, в частном они могут быть одинаковыми.

Определение 27. Математическим определением дискретной случайной величины ξ (М{ξ} или m_ξ) называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

М{ξ} = Х₁Р₁+Х₂Р₂+ … Х _n Р _n = [3.1]

при этом

Для бесконечной последовательности значений ξ

[3.2]

Математическое ожидание М{ξ} числа появление соотношения А при n независимых испытаний равно произведению числа искажений на вероятность появления события А при каждом испытании

М{ξ} = nр [3.3]

Заметим, что при → 1 при р → 1

→ ∞ при р → 0

Математическое ожидание случайной величины ξ называется центром распределения вероятности случайной величины.

Центр распределения вероятностей введен по аналогии с «центром тяжести»

Определение 28. Разность случайной величины ξ и ее м.о. ξ - называют центрированной случайной величиной или отклонением и обозначают ξ⁰

Определим м.о. центрированной с.в.

М [ξ - ] = [3.4]

М.о. центрированной с.в. равно нулю

М [С] = С 1 = С М.о. постоянной равно самой постоянной

1.2. Дисперсия. Среднее квадратическое отклонение.

Понятие о моментах

Математическое ожидание определяет центр распределения вероятностей случайной величины. Дисперсия означает рассеивание относительной центральной величины.

Означают D_ξ ; D {ξ}

Определение 29. Дисперсия случайной величины ξ называется математическое ожидание квадрата разности случайной величины ξ и ее математического ожидания (т.е. математическое ожидание квадрата соответствует центрированной случайной величины).

D [ξ ] = М_n [(x – m_ξ)]² [3.5]

D [ξ ] = (x – m_ξ)² P_R [3.6]

Размерность дисперсии квадрат случайной величины.

Определение 30. Средним квадратическим отклонением случайной величины называется корень квадратный из ее дисперсии

δ (ξ) = { ξ } или

δ (ξ) = { ξ } = [3.7]

Дисперсию удобно преобразовать:

D [ξ ] = (Х_k – m_ξ)² P_R = (Х_k – m_ξ)² X_k²P_k - 2 Х_k – m_ξ P_{R +} m_ξ² P_k =

= M { ξ ²} - 2 m_ξ m_ξ+ m_ξ²1 = M { ξ ²} - m_ξ² = _X – m_ξ)² P_R [3.8]

Поясним смысл понятия дисперсию, ее наглядную интерпретацию на примере:

1 . Дано: Случайная величина ξ которая носит дискретный характер и задается в виде таблицы ξ 2 3 4

Рk 0,3 0,4 0,4

Рис. 3.2.

Определить: 1. Математическое ожидание

2. Дисперсию

3. Среднее квадратическое отклонение

Решение:

1. M {ξ} = 2. 0,3 + 3 .0,4 + 4 . 0,3 = 3

2. D{ξ} =(3.3)² .0,3 + (3-3)². 0,4 = (4-3)².0,3 = 0,6

3. δ {ξ} = {ξ} = 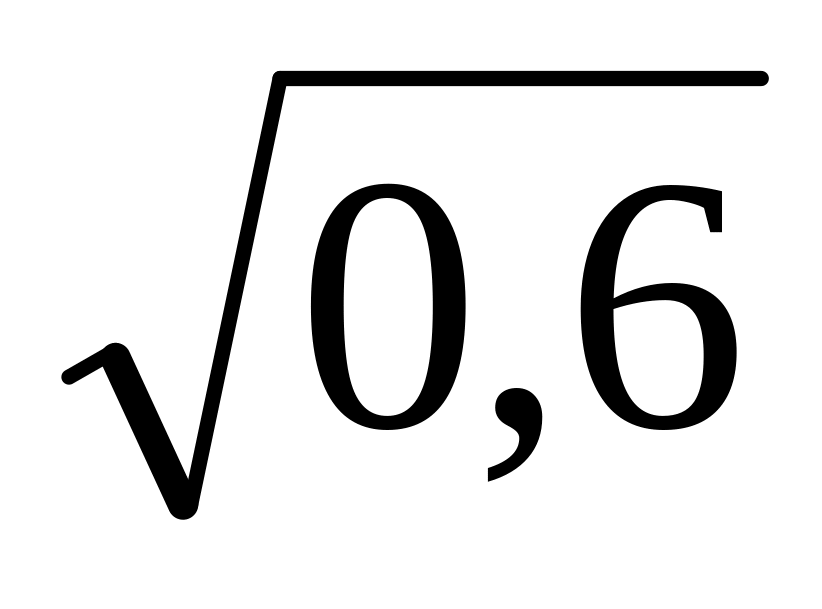= 0,77

Дано: Величина ξ, которая принимает следующие значения

ξ 1 3 5

Р _R 0,3 0,4 0,3

Определить M {ξ} = ? D{ξ} - ? δ {ξ} - ? Рис.3.3.

1. M {ξ} = Х_R P_R = 1 / 03 + 04 + 5/03 = 3

2. D{ξ} = (Х_R – m_ξ)² P_R=(1-3)².0,3+(3-3)².0,4 + (5-3)².0,3 = 2,4

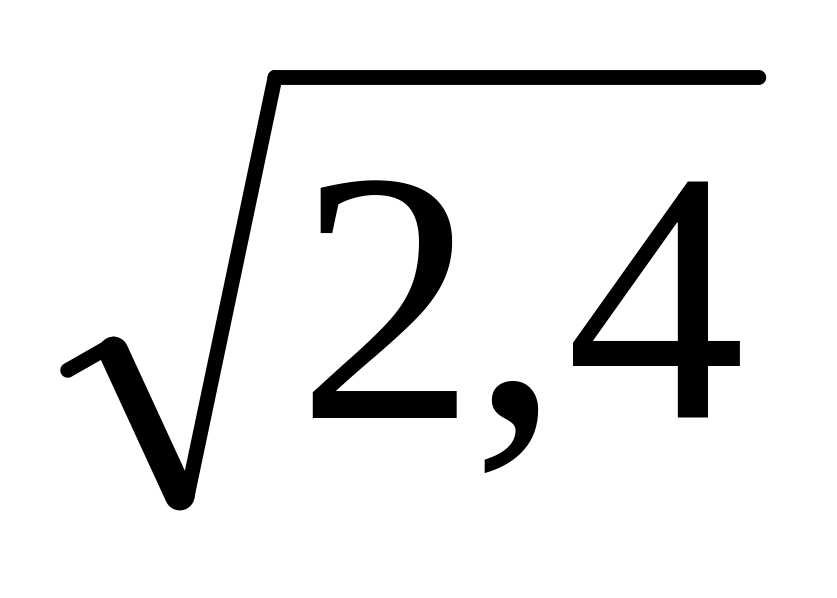3. δ {ξ} = = 1,55

Как видно из примеров 1 и 2 математическое ожидание для ξ₁ и ξ₂ одинаковы, а дисперсии различны. Для второго случая разброс относительно математического ожидания почти в два раза больше, что видно также визуально из анализа рис. 3,2 и 3.3.

Из определения дисперсии также следует, что дисперсия постоянной величины С, D [С] = 0

D [С] = М[(С- С)²] = М(С) = 0 [3.8]

Определение 30. Центральным моментом первого порядка называют М(х- m_ξ), математическое ожидание величины (х- m_ξ)² называют центральным моментом второго порядка, (х- m_ξ)³ – соответственно центральным моментом третьего порядка, (х- m_ξ) – центральным моментом первого порядка.

• ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНОЙ

СЛУЧАЙНОЙ ВЕЛИЧИНЫ

По аналогии, как для дискретной случайной величины определим числовые характеристики для непрерывной случайной величины - т.е. математическое ожидание, дисперсию, среднее квадратическое отклонение.

Основные понятия и термины.

1. Математическое ожидание непрерывной случайной величины M {ξ}

2. Центр распределения центрирования случайной величины.

3. Среднее квадратическое непрерывной случайной величины и дисперсия.

4. Мода случайной величины.

5. Модели случайной величины

6. Унимодельная, бимодельная

Рассмотрим числовые характеристики непрерывной случайной величины ξ с плотностью вероятности ƒ(х).

Определение 31. Математическим ожиданием непрерывной случайной величины ξ с плотностью распределения вероятности ƒ(х) называется выражение.

M {ξ} = [3.9]

если случайная величина ξ лежит в интервале [а;в] то

M {ξ} = [3.10]

математическое ожидание может принимать любое значение на интервале {а;в}

Обозначают: M {ξ} или m_ξ

Определение 32. Математическое ожидание называют центром распределения вероятностей случайной величины ξ, или кривая распределена симметрично относительно оси 0у, т.е. функция ƒ(х) четная

M {ξ} = = 0 [3.11]

Рис 3.4.

Определим центрированную случайную величину как ξ - m_х

М [ξ-m_ξ] = [3.12]

т.е. математическое ожидание дестрированной случайной величины равно 0

Определение 33. Дисперсией непрерывной случайной величины ξ называется математическое ожидание квадрата соответствующей центрированной случайной величины.

D{ξ} = [3.13]

Определение 34. Средним квадратическим случайной величины ξ называется корень квадратный из дисперсии, с.к.о. имеет размерность случайной величины

υ{ξ} = {ξ} = [3.14]

Определение 35. Значение случайной величины ξ, при котором плотность распределения имеет наибольшее значение, называется любой и обозначается М₀ = X_m= X max

Определение 36. Число, которое называется медианой, должно удовлетворять равенству

Рис.3.5.

т.е. медиана есть такое значение Хе случайной величины ξ при котором площадь под плотностью вероятности делится пополам.

На рисунке 3.6. наглядно видно как определены математическое ожидание , медиана Хе, мода Х ; для различных плотностей вероятностей имеющих несимметричный и симметричный характер.

Рис. 3.6.

Определение 37. Если плотность распределения имеет:

Один максимум, то она называется унимодальной

Два максимума бимодельной пл. распределитель вероятной

n максимумов медиамодальной.