Лекция 12. Случайные процессы в линейных системах

Цель лекции:

• ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПЕЙ.

ЗАДАЧИ АНАЛИЗА

Основные определения и термины.

1. Импульсные характеристики

2. Переходная характеристика

3. Передающая функция

4. Комплексная частотная характеристика

Линейные системы осуществляют линейное преобразование входного сигнала в выходной. Полное описание поведения любой линейной системы при заданных начальных условиях дается решением соответствующего линейного дифференциального уравнения. Однако иногда для этих целей можно использовать импульсные и переходные характеристики, а также передаточными функциями и комплексами частотными характеристиками, которые связаны друг с другом.

Определение Импульсная характеристика линейной системы h(t) представляет собой выходной сигнал системы при входном сигнале в виде дельта – функции δ(t) и нулевых начальных условиях.

Определение Переходная характеристика q(t) – есть выходной сигнал системы с нулевыми начальными условиями при входном сигнале, имеющем вид единичной функции: 1(t) = 0 при t < 0 и 1(t) = 1 при t > 0

Импульсная и переходная характеристика связаны друг с другом соотношениями

[12.1]

[12.2]

Определение Переходная функция линейной системы К(р) является преобразованием Лапласа от импульсной характеристики

[12.3]

где р = α + jω

Определение Комплексная частотная характеристика К(jω) представляет собой преобразование Фурье от импульсной характеристики:

[12.4]

где /К(jω)/ - амплитудно-частотная характеристика

ωq К(jω) – фазочастотная характеристика системы

Из обратного преобразования Фурье следует выражение импульсной характеристики через комплексную частотную характеристику:

[12.5]

Из физических соображений ясно, что выходной сигнал не может упреждать входной, т.е. при t < 0, и, кроме того, для устойчиво работающих систем

<

Этот результат обычно формулируют в виде двух эквивалентных условий физически возможной линейной системы:

при t < 0 <

< [12.6]

В дальнейшем будут рассматриваться в основном линейные стационарные системы (системы с постоянными во времени параметрами), в которых сдвиг входного сигнала во времени приведет к такому же сдвигу выходного сигнала. В качестве определяющих характеристик таких систем будем использовать импульсные и комплексные частотные характеристики.

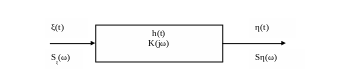
Рис. 2.

Пусть на вход линейной системы (рис.2), начиная с момента времени t₀ воздействует случайный процесс (сигнал) ξ(t) со спектральной плотностью S_ξ(ω), причем начальные условия нулевые тогда выходной случайный процесс (сигнал) η(t) определяется интегралом Дюамеля.

[12.7]

Если при t = t₀ начальные условия в системе не нулевые , то результирующий выходной процесс будет содержать дополнительные слагаемые, обусловленные, «затуханием начальных условий».

Начальные условия могут быть как детерминированными (фиксированными), так и случайными. Сформулируем следующую, достаточно общую задачу анализа.

Пусть на вход линейной системы с заданной импульсной характеристикой воздействует случайный процесс ξ(t) с известной плотностью вероятности р_ξ(ξ₁ ξ₂ ξ₃ . . . ξR; C₁; t₂ . . . t_n). Требуется найти плотность вероятности выходного случайного сигнала η(t)

рη (η₁ η₂ . . . ηℓ; t₁ t₂ . . . t_ℓ) ℓ<k

В общем случае не существует прямого и достаточно простого момента, который позволил бы находить непосредственно плотности вероятности для выходного сигнала η(t). Здесь исключение составляют гауссовские и марковские процессы.

Сформулированную задачу приходится решать следующим образом: При помощи формул вычисляют начальные или центральные моменты (корреляционные функции) входного процесса ξ(t). Затем по моментным или корреляционным функциям входного процесса ξ(t) находят моментные или корреляционные функции выходного процесса η(t).

Применительно к гауссовским процессам задача упрощается, т.к. выходной процесс также носит гауссовский характер.

Если выходной процесс η(t) – является Марковским, то плотность вероятности р_η можно получить, решая соответствующе уравнение Фоккера – Планка – Колмогорова.

При решении задач в рамках корреляционной теории часть можно ограничиться вычислением математического ожидания и корреляционной функции выходного процесса.

• ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНОЙ СЛУЧАЙНОЙ ФУНКЦИИ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМОЙ

Общие правила линейных преобразований случайных процессов (сигналов, функций) сводятся к тому, что при линейных преобразованиях случайных процессов их математические ожидания и корреляционные функции подвергаются тем же линейным преобразованиям. В случае, когда речь идет о линейных, преобразования стационарных случайных процессов, задача практически может быть сведена к преобразованию – спектральной плотности входного сигнала S_ξ(ω).

Для того, что бы реакция системы при стационарном воздействии на входе была стационарна необходимо, что бы входящие в нее сопротивления, емкости, индуктивности и т.п. были постоянными, а не пер еменными. Условимся называть линейную систему с постоянными параметрами стационарной линейной системой. Обычно работа стационарной линейной системы описывается дифференциальными уравнениями с постоянными коэффициентами.

Рассмотрим задачу о преобразовании стационарного случайного процесса стационарной линейной системой.

Дано: На вход линейной стационарной системы поступает входной стационарной сигнал ξ(t) с известными заранее математическим ожиданием m_ξ и корреляционной функцией R_ξ(t).

Определить: Характеристики случайного сигнала на выходе линейной системы.

Определим реакцию системы Т на неслучайное воздействие ξ(t), для чего напишем в операторной форме линейное дифференцированное уравнение с постоянными коэффициентами, связывающее входное и выходное воздействие.

[12.8]

где - оператор дифференцирования

или Аn(p)η(t) = Bm(p)ξ(t) [12.9]

Разрешая уравнение [12.9] относительно входного воздействия имеем:

[12.10]

Для анализа реакции системы Т в качестве входного воздействия возьмем гармоническое колебание следующего вида

[12.11]

Очевидно, что реакция системы Т, также будет представлять собой гармоническое колебание умноженное на частотную характеристику системы.

[12.12]

Определим следующим образом, подставим уравнение [12.11] и [12.12] в выражение [12.8]

[12.13]

Исходя из математических соотношений имеем:

и разделив обе части уравнения [12.13] на е^jωt получим

К(jω) [α_n(jω)⁷+α_n-1(jω)^n-1+ …α₁(jω)+α₀] = b_m(jω)^m+b_m-1(jω) + . . . b₁(jω)+b₀ [12.14]

Проведя сравнительный анализ [12.14] и [12.8] и [12.9] видим, что множитель К(jω) представляет ни что иное как многочлен.

А_n(P) в котором вместо оператора дифференцирования р подставлено выражение (jω) аналогично и для Вm(Р).

Тогда [12.9] запишем как:

К(jω) А_n(jω) = Вm(jω) [12.15]

Откуда

[12.16]

Данная функция носит специальное название частотной характеристики. Для определения частотной характеристики достаточно в оператор системы, записанной в таком виде [12.10], вместо оператора дифференцирования Р подставить jω.

Таким образом, если на вход линейной системы с постоянными параметрами поступает гармоническое колебание вида е^jωt, то реакция системы представляется в виде того же гармонического колебания, умноженного на частотную характеристику

Если на вход системы поступает воздействие вида

ξ(t) = Ue^jωt [12.17]

где U – некоторая величина не зависящая от t то величина U выходит за знак оператора, а реакция системы будет равна:

η(t) = UK_(jω)e^jωt [12.18]

Применим изложенные приемы преобразования гармонических колебаний линейной системой к математическому ожиданию случайной функции ξ(t) и координатным функциям ее спектрального разложения.

1. Несовместимые случайные события

2. Полная группа случайных событий

3. Равновозможное случайное событие. Случай (шанс)

4. События благоприятствующие. Классическое определение вероятно.

5. Достоверное событие

6. Невозможное событие

7. Сумма двух событий А₁ и А₂ (несовместимых событий)

8. Противоположные события

9. Совместные случайные события А и В их сумма

10. Геометрическая вероятность

11. Независимые события

12. Вероятность независимых событий

13. Зависимые события

14. Условные вероятности. Вероятность совмещения двух событий.

15. Полная вероятность

16. Гипотеза

17. формула гипотез Байссек).

18. Дискретная случайная величина

19. Закон распространения дискретной случайной величины

20. Способ задания закона распространения дискретной случайной величины (СВ)

21. Мода случайной величины.

22. Непрерывная случайная величина ξ

23. Плотность распределения вероятностей случайной величиной или закон распределения непрерывной а в, или плотность распределения, плотн6ость вероятности Ру

24. Свойства плотности вероятностей, элемент вероятности Р_(х)Δу

25. Функция распределения случайной величины F_(х)

26. Математическое ожидание дискретной с.в.

27. Центр распределения вероятностей с.в.

28. Центрированная с.в. ξ - m _ξ или отражение

29. Дисперсия

30. Математическое ожидание непрерывной случайной величины M {ξ}

31. Центр распределения центрирования случайной величины.

32. Среднее квадратическое непрерывной случайной величины и дисперсия.

33. Мода случайной величины.

34. Модели случайной величины

35. Унимодельная, бимодельная

36. Плотность определения двумерной случайной величины

37. Интегральная функция распределения вероятностей второй с.в.

38. Математическое ожидание, дисперсия среднее квадратическое отклонение второй с.в.

39. Начальный момент порядка К, S

40. Центральный момент порядка К, S

41. Корреляционный момент

42. Коэффициент корреляции

43. Многомерная функция распределения вероятностей случайной величины. Плотность вероятности или совместная плотность вероятности.

44. Условия неотрицательности, условие нормировки, условие согласованности, условие симметрии.

45. Математическое ожидание вектора случайной величины

46. Совместные начальные моменты m_v1, m_v1v2, m_v1v2v3

47. Центральные моменты первого порядка

48. Гауссовская случайная величина, нормальный закон распределения

49. Функция распределения гауссовской случайной величины.

50. Основные процессы

51. Реализация случайного процесса (Траектория СП) выборочная функция

52. Случайная функция ξ(t)

53. Детерминирование функции

54. Соединение поля (Многомерные сигналы)

55. Скалярный случайный процесс.

56. Векторный случайный процесс

57. Скалярное случайное поле

58. Стационарные и нестационарные случайные процессы в узком смысле

59. Стационарный случайный процесс в широком смысле.

60. Эргодические и неэргодические стационарные случайные процессы

61. Абсолютно случайный процесс.

62. Интенсивность абсолютного случайного процесса

63. «Белый шум».

64. Импульсные характеристики

65. Переходная характеристика

66. Передающая функция

67. Комплексная частотная характеристика