1.5. Экстремум функции одной переменной

Говорят, что точка х₀ является точкой строгого локального максимума (минимума) заданной функции f(x), если существует такая  - окрестность точки х_0, что для любой точки х из этой  - окрестности, х  х_0, выполняется условие f(x)  f(x₀) (f(x)  f(x₀)). При замене знака  на  получается определение для нестрогого локального максимума (минимума).

В этом разделе для краткости будем писать просто «максимум (минимум) функции», имея в виду локальный максимум (локальный минимум) функции.

Максимум или минимум функции называют собирательным термином экстремум функции.

Пример 1.8.

1) Функция имеет в точке х₀ = 0 строгий локальный максимум, но локальных минимумов она не имеет.

2) Функция f(x) = sin x имеет в точках , k = 0, 1, 2,,строгие локальные максимумы равные 1, а в точках , k = 0, , 1, 2, - строгие локальные минимумы, равные –1.

Теорема Ферма (необходимое условие экстремума (строгого и нестрогого) дифференцируемой функции). Если действительная функция f(x) определена в окрестности точки х_0, дифференцируема в этой точке и имеет в ней экстремум, то ее первая производная в точке х₀ равна 0: f'(x₀) = 0

Достаточное условие строгого экстремума дифференцируемой функции. Если действительная функция f(x) определена в окрестности точки х₀, дважды дифференцируема в этой точке и имеет в ней нулевую первую производную f^'(x₀) = 0, а также отрицательную (положительную) вторую производную f"(x₀)  0 (f"(x₀)  0), то функция f(x) достигает в х₀ своего строгого максимума (минимума)

Для геометрической интерпретации условий существования экстремума дифференцируемой функции полезным оказывается понятие выпуклости графика этой функции и его связь со знаком второй производной.

График функции f(x) называется выпуклым вверх (вниз) на интервале (a, b), если он целиком расположен не выше (не ниже) любой касательной к нему на интервале (a,b). Если, кроме того, график имеет не более одной общей точки с любой касательной к нему на интервале (a,b), то он называется строго выпуклым.

Если график дважды дифференцируемой функции f(x) строго выпуклый вверх (вниз) на интервале (a,b), то f"(x)  0 (f"(x)  0) на этом интервале; верно и обратное

Теперь проиллюстрируем условия существования строгих экстремумов.

Пусть действительная функция f(х) имеет в точке х₀ строгий локальный максимум, дважды дифференцируема в некоторой окрестности точки х₀ и имеет строго выпуклый вверх график (см. рис. 1.6). Поскольку f(x₀) является наибольшим значением функции в этой окрестности, то по теореме Ферма в точке х₀ f'(x₀) = 0 и касательная в ней горизонтальна. В силу строгой выпуклости графика первая производная в точках х_1, х₂ должна быть положительна, а в точках х₃ и х₄ должна быть отрицательна. Более того, первая производная должна монотонно убывать в этой окрестности, т.е. , поскольку , а . Именно поэтому вторая производная функции f(х), которая имеет смысл скорости изменения первой производной, должна быть в этой окрестности отрицательной, т.е. . В частности, f"(x₀)< 0.

Иллюстрация для случая строгого локального минимума представлена на рис. 1.7. Рассуждения, аналогичные предыдущему случаю, приводят нас к выводу, что первая производная должна строго возрастать, т.е. tg ₁  tg₂  0, а 0 < tg₁  tg₂, принимая нулевое значение в точке х₀, f'(x₀) = 0.

Поэтому вторая производная функции f должна быть в окрестности точки х₀ положительной, . В частности, f"(x₀) > 0.

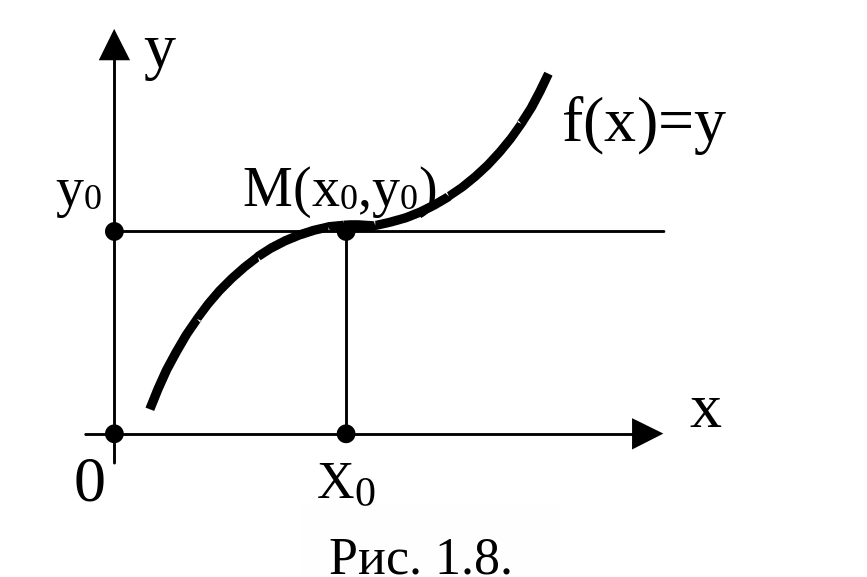
На рис. 1.8 изображен случай, когда функция f(x) имеет в точке х₀ нулевую производную (геометрически это означает, что касательная к графику в точке М (х₀ ,y₀) горизонтальна), но точка х₀ не является точкой экстремума, поскольку в этой точке (действительно, левее х₀ , а правее х₀ , чему геометрически соответствует разное направление строгой выпуклости графика). Данное обстоятельство иллюстрирует важность понятия так называемых точек перегиба.

Пусть функция f определена в некоторой окрестности точки х₀ и дважды дифференцируема в этой окрестности. Точка х₀ называется точкой перегиба функции f, если она одновременно является концом интервала строгой выпуклости вверх ) и концом интервала строгой выпуклости вниз ( .

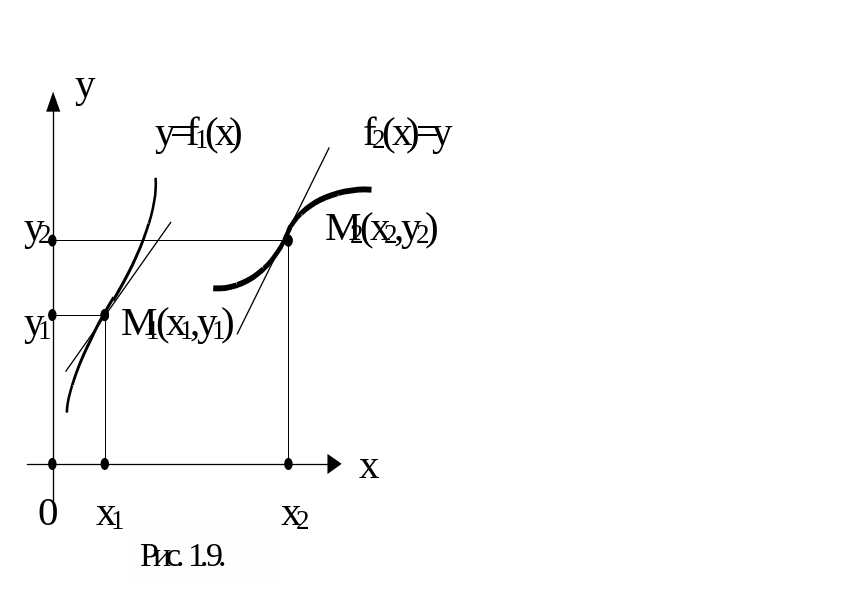
На рис.1.8 график функции «перегибается» через касательную к нему в точке М (х₀, y₀=f(x₀)). На рис. 1.9 при х < x₁ график функции f₁(x) лежит под касательной, а при х > х₁ – над ней; наоборот, при х < x₂ график функции f₂(x) лежит над касательной, а при х >x₂ – под ней.

Необходимое условие существования точки перегиба – равенство 0 второй производной в этой точке, т.е. . Достаточное условие точки перегиба: и 