1.2 Задачи с решениями

Задача 1.2.1. Определить объем воды, который необходимо дополнительно подать в водовод диаметром d = 500 мм и длиной l = 1 км для повышения давления до ∆р = 5·10⁶ Па. Водовод подготовлен к гидравлическим испытаниям и заполнен водой при атмосферном давлении. Деформацией трубопровода можно пренебречь.

Решение. Вместимость водовода

.

Объем воды ∆V, необходимый для подачи в водовод для повышения давления, найдем из соотношения для коэффициента объемного сжатия

.

Значения коэффициента объемного сжатия воды β_V (Па^-1) в функции от давления и температуры примем по таблице 1.5:

тогда

.

Задача 1.2.2. В гидравлической системе содержится объем воды V = 0,4 м³. Сколько воды дополнительно войдет в расширительный сосуд при нагревании ее с 20 до 90 ⁰С?

Решение.

Плотность воды при температуре 20 ⁰С определим по таблице 1.5 ρ₂₀ = 998 кг/м³, тогда масса воды М = V·ρ = 0,4·998 = 399 кг.

Плотность воды при температуре 90 ⁰С равна ρ₉₀ = 965 кг/м³, тогда объем, занимаемый водой при t = 90 °С, составит

.

Дополнительный объем составит ∆V= 0,414 - 0,4 = 0,014 м³.

Задача 1.2.3. Определить среднюю толщину δ_отл солевых отложений в герметичном водоводе с внутренним диаметром d= 0,3 м и длиной L = 2 км (рисунок 1.1), если при выпуске воды в объеме ∆V = 0,05 м³ давление в водоводе падает на величину ∆р = 1·10⁶ Па. Отложения по диаметру и длине водовода распределены равномерно.

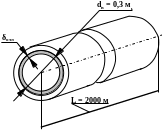
Рисунок 1.1. Схема отложений в поперечном сечении трубы

Решение. Объем воды в водоводе с отложениями

.

Коэффициент объемного сжатия воды таблице 1.5

тогда

.

Средний внутренний диаметр водовода с отложениями

Средняя толщина отложений

Задача 1.2.4. Определить изменение плотности воды при ее сжатии от р₁ = 1·10⁵ Па до р₂ = 1·10⁷ Па.

Решение. Примем коэффициент объемного сжатия воды β_V = 5·10^-10 Па^-1. Как известно, плотность воды: ρ = M/W. При сжатии воды ее объем V изменится на величину ∆V:

,

где

Δр = р₁ - р₂ =1·10⁵ -1·10⁷ =- 0,99·10⁷.

Так как масса воды останется неизменной, поэтому

Задача 1.2.5. Для периодического аккумулирования дополнительного объема воды, получаемого при изменении температуры, к системе водяного отопления в верхней ее точке присоединяют расширительные резервуары, сообщающиеся с атмосферой. Определить наименьший объем расширительного резервуара при частичном заполнении водой. Допустимое колебание температуры воды во время перерывов в работе топки ∆t = 95 - 70 = 25 ⁰С. Объем воды в системе V= 0,55 м³.

Решение. Наименьший объем расширительного резервуара должен быть равен изменению объема воды при повышении ее температуры на 25 ⁰С. Изменение объема найдем по формуле для коэффициента температурного расширения β_t (⁰С^-1), отражающего относительное изменение объема жидкости при изменении температуры на 1 ⁰С:

,

где ∆V - изменение объема воды, соответствующее изменению температуры на величину Δt.

Для воды в соответствии с таблицей 1.5 можно принять:

- при нормальных условиях ;

- при температуре 80 ⁰С .

Тогда

ΔV = β_t V·Δt = 600·10^-6 ·0,55·25 = 0,0083 м³ = 8,3 л.

Задача 1.2.6. В нагревательный котел поступает объем воды V= 50 м³ при температуре 70 ⁰С. Какой объем воды V₁ будет выходить из котла при нагреве воды до температуры 90 ⁰С?

Решение. Из формулы коэффициента температурного расширения имеем: ∆V=β_t V·∆t.

Коэффициент температурного расширения воды по таблице 1.5 β_t = 600·10^{-6 0}С ^-1, следовательно, ∆V= 600·10^-6 ·50·20 = 0,6 м³. Тогда V₁ = 50 + 0,6 = 50,6 м³.

Задача 1.2.7. Определить изменение плотности воды при нагревании ее от t₁ = 7 ⁰С до t₂ = 97 ⁰С.

Решение. Примем коэффициент температурного расширения воды: β_t ~ 400·10^{-6 0}С ^-1 . При нагревании воды от t₁ = 7 ⁰С ее объем изменится на ∆V.

Тогда из формулы коэффициента температурного расширения имеем ∆V/V= β_t·∆t. Плотность воды ρ = M/V. Учитывая, что масса воды М сохраняется неизменной, найдем

Задача 1.2.8. Вязкость нефти, определенная по вискозиметру Энглера, составляет 8,5 ⁰Е. Вычислить динамическую вязкость нефти, если ее плотность ρ = 850 кг/м³.

Решение. Найдем кинематическую вязкость нефти по эмпирической формуле Убеллоде:

.

Кинематическую вязкость измеряют также в стоксах. Так как

1 Ст = 1·10^-4 м²/с, то ν = 0,614·10^-4 Ст.

Проверим полученный результат по теоретической формуле Альтшуля:

,

где С₁ и С₂ - экспериментальные коэффициенты, равные:

Подставив в формулу Альтшуля С₁ и С₂, получим:

Для кинематической вязкости функции ⁰Е = 8,5 соответствует ν = 0,6139·10^-4 м²/с.

Динамическая вязкость нефти μ=ν·ρ= 0,614·10^-4·850 = 0,052 Па·с.

Динамическую вязкость измеряют также в пуазах. Так как 1 П = 0,1 Па·с, то μ = 0,052 Па·с = 0,52 П.

Задача 1.2.9. Определить давление внутри капли воды диаметром d = 0,001 м, которое создают силы поверхностного натяжения. Температура воды t = 20 ⁰С.

Решение. Давление внутри капли определим по формуле Лапласа для криволинейных поверхностей:

,

где σ - поверхностное натяжение, определяемое по формуле для воды при t = 20 ⁰С, соприкасающейся с воздухом, σ = 0,0726 Н/м; r - радиус капли.

Тогда

.

Задача 1.2.10. Как изменится плотность бензина А76, если температура окружающей среды изменится с 20 до 70 ⁰С?

Решение. Плотность нефтяных продуктов в зависимости от температуры определяется по формуле:

,

где β_t - коэффициент температурного расширения, учитывающий относительное изменение объема жидкости при изменении температуры на 1 ⁰С; для нефтепродуктов β_t = 0,0006 ⁰С^-1; ρ₂₀ - плотность бензина А76 при t=20 ⁰С; ρ₂₀ = 800 кг/м³ (табличная величина), ρ₇₀ = 776,7 кг/м³.

Следовательно, изменение плотности бензина при повышении температуры с 20 до 70 ⁰С будет равно 776,7/800 = 0,97, т.е. плотность уменьшится на 3 %.

Задача 1.2.11. Как изменятся объемный вес и плотность воды друг относительно друга на экваторе и Северном полюсе?

Решение. Примем среднюю годовую температуру на полюсе примерно 0 ⁰С, а на экваторе 40 ⁰С.

Тогда, согласно справочным таблицам, для воды:

ρ₄₀ = 992,2 кг/м³, а ρ₀ = 999,87 кг/м³,

.

Следовательно, плотность уменьшится в 0,99 раза.

Ускорение силы тяжести на экваторе g_экв = 9,781 м/с², а на полюсе g_пол = 9,831 м/с². Тогда объемный вес воды:

- на экваторе γ_экв = ρ₄₀·g_экв = 992,2·9,781 = 9704,70 Н/м³;

- на полюсе γ_пол = ρ₀·g_пол = 999,87·9,831 = 9829,72 Н/м³.

Следовательно, γ_пол/γ_экв ⁼ 9829,72/9704,72 = 1,013, т.е. объемный вес воды увеличится на полюсе в 1,013 раза.