2.5 Определение модального интервала распределения и вычисление моды

Для характеристики структуры совокупности применяются особые показатели, которые называются структурными средними. К таким показателям относятся мода и медиана.

Модой (М_о) называется вариант, наиболее часто встречающийся в данном ряду.

Это применимо для дискретного ряда.

В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту (частость).

Конкретное значение моды для интервального ряда определяется формулой:

М_о = х_мо + i_мо

где Х_мо – нижняя граница модального интервала;

i_мо – величина модального интервала;

f_мо – частота, соответствующая модальному интервалу;

f_мо-1 – частота, предшествующая модальному интервалу;

f_мо+1 –частота интервала, следующего за модальным.

Определяем модальный интервал и рассчитываем моду по данным таблицы 3.

2.6 Определение медианного интервала распределения и вычисление медианы

Медианой в статистике называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Для ранжированного ряда (т.е. построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом членов медианой является варианта расположенная в центре ряда.

Для ранжированного ряда с четным числом членов медианой будет средняя арифметическая из двух смежных центральных значений.

В интервальном вариационном ряду медиана рассчитывается на основе кумулятивных (накопленных) частот, под которыми понимается нарастающий итог частот, начиная с первого интервала.

Формула исчисления медианы для интервального вариационного ряда будет иметь такой вид:

М_е= х_ме+i_ме

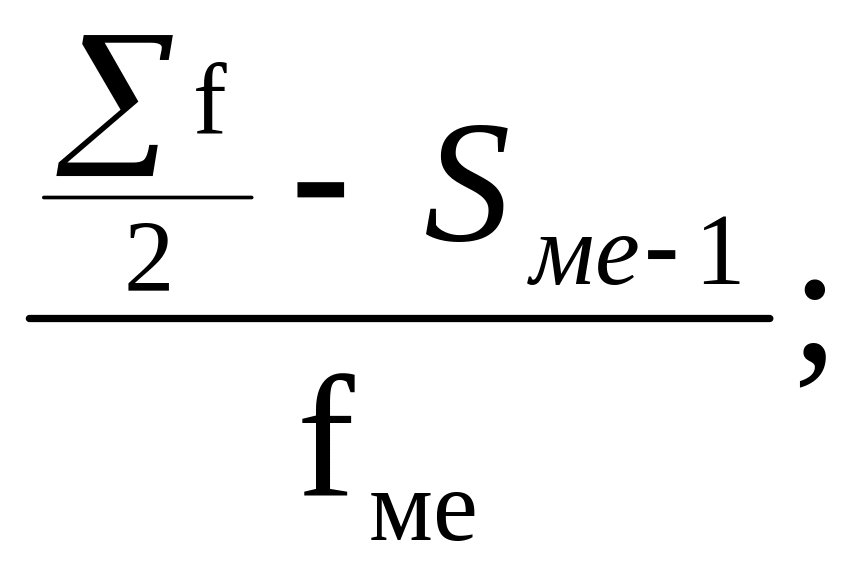
где х_ме – начальное значение медианного интервала; i_ме – величина медианного интервала; ∑f – сумма частот ряда; S_ме-1 – сумма накопленных частот в интервалах, предшествующих медианному; f_ме – частота медианного интервала.

Для определения медианы строим рабочую таблицу 4

Таблица 4 Данные для определения медианы

№ группы	Группы предприятий по величине стоимости основных фондов, млн. руб xi	Число предприятий шт., (частоты) fi	Кумулятивные (накопленные) частоты
	Итого

Медианным является интервал, кумулятивная частота которого равна или превышает половину суммы частот.

2.7 Расчет и анализ абсолютных показателей вариации

Полученные в процессе статистического наблюдения величины того или иного признака у отдельных единиц совокупности различаются между собой.

Колеблемость, многообразие, изменяемость величины признака у единиц совокупности называется вариацией.

Вариация порождается комплексом условий, действующих на совокупность и ее единицы.

Вариация существует во времени и в пространстве. Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям. Вариация во времени – это изменение значений признака в различные периоды или моменты времени.

По степени вариации можно судить об однородности совокупности , устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления, и признаками разных явлений.

Статистические показатели, характеризующие вариацию, широко применяются в практической деятельности, например, для контроля за ходом производственных процессов, для оценки ритмичности работы промышленных предприятий.

Показатели вариации делятся на две группы: абсолютные и относительные.

К абсолютным относятся:

- размах вариации;

- среднее линейное отклонение;

- дисперсия;

- среднее квадратическое отклонение.

Относительными показателями являются:

- коэффициент осцилляции;

- линейный коэффициент вариации;

- коэффициент вариации.

Р азмах вариации показывает, насколько велико различие между максимальными и минимальными значениями признака. Его рассчитывают следующим образом:

R=х_max-х_min;

где х_max – максимальное значение варьирующего признака;

х_min – минимальное значение варьирующего признака.

Для анализа вариации, кроме размаха вариации, необходим еще показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику вариации. Все то общее, что свойственно всем единицам совокупности, находит отражение в средних величинах. Однако каждой единице свойственны и индивидуальные особенности, которые ведут к отклонениям от среднего уровня. Следовательно, средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание значений признака. При обобщении этих колебаний необходимо найти среднюю величину этих отклонений.

Такая средняя называется средним линейным отклонением ( ). Оно определяется как средняя арифметическая из отклонений индивидуальных значений признака от средней без учета знака этих отклонений:

= ;

По приведенной формуле рассчитывается простое (невзвешенное) среднее линейное отклонение.

Для вариационного ряда с неравными частотами используют формулу взвешенного среднего линейного отклонения:

=

где х_i – варианты признака; – средняя величина; f_i – частоты.

Таким образом, среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности. Этот показатель более обоснован по сравнению с размахом вариации, так как он не зависит от случайных колебаний вариантов и учитывает всю сумму отклонений вариантов от средней величины. Суммирование показателей без учета знака в ряде случаев имеет экономический смысл. Например, общий оборот рабочей силы определяется, как сумма принятых и уволенных, оборот внешней торговли как сумма экспорта и импорта и т.д. Однако при исчислении среднего линейного отклонения приходится допускать некорректные с точки зрения математики действия.

Поэтому более широкое распространение получили обобщающие показатели вариации, рассчитанные с использованием вторых степеней отклонений. К этим показателям относятся дисперсия и среднее квадратическое отклонение.

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака и от их величины. Обозначается дисперсия греческой буквой ² (сигма в квадрате) и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

²= – простая дисперсия;

²= - взвешенная дисперсия.

Среднее квадратическое отклонение равно корню квадратному из дисперсии:

= =

Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах измерения, что и признак (рублях, метрах, тоннах, процентах т.д.)

Смысловое содержание среднего квадратического отклонения такое же, как и среднего линейного отклонения, чем меньше , тем следовательно , однороднее совокупность, типичнее средняя и более устойчивое явление или процесс.

Приведенные формулы исчисления среднего линейного и квадратического отклонения относятся к случаям, когда эти показатели определяются на основе либо отдельных наблюдений, либо дискретного ряда распределения.

В статистике чаще всего приходится исчислять такие показатели по интервальным рядам. Такой расчет отличается от аналогичного расчета по дискетному ряду распределения лишь тем, что требует предварительного определения середины интервала.

Серединные значения интервалов определяются как простые средние арифметические из двух крайних значений интервалов.

Для расчета и анализа абсолютных показателей вариации необходимо построить рабочую таблицу 5

Таблица 5 Исходные и расчетные данные для определения абсолютных показателей вариации.

Группы предприятий по величине стоимости основных фондов, млн. руб. хi	Число предприятий fi	Расчетные показатели
		Х1i	Х1i fi	[хi- ]	[хi- ]fi	(хi- )2	(хi- )2* fi
А	1	2	3	4	5	6	7
Итого		-		-