3.1.2 Симплекс-метод решения задачи

Рассмотрим теперь решение задачи с параметром в целевой функции симплекс-методом.

Возьмем фиксированное значение параметра L=L₀. Пусть для этого значения получена оптимальная симплексная таблица. Поскольку коэффициенты целевой функции зависят от параметра, элементы критериальной строки также будут представлять собой выражения, содержащие параметр. Рассмотрим симплексную таблицу для такой задачи^* (таблица 3).

Таблица 3 – Симплексная таблица

				c1`+ Lc1``	. . .	cj`+ Lcj``	. . .	cn`+ Lcn``
№	xб	cб	В	х1	. . .	хj	. . .	хn
1	. . .	. . .	b1	a 11	. . .	a 1j	. . .	a1n
. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .
m	. . .	. . .	bm	a m1	. . .	a mj	. . .	amn
m+1			d`+Ld``	1`+L1``	. . .	j`+Lj``	. . .	n`+Ln``

Сравним выражения в критериальной строке с нулем (проверим выполнение критерия оптимальности). На промежутке изменения L, на котором заключительная таблица остается оптимальной, полученный результат останется решением задачи.

(4)

(если задача на максимум, иначе - ).

В полученных неравенствах перенесем свободный член _j` в правую часть и разделим обе части на (при этом если _j``< 0, то знак неравенства меняется не противоположный).

(5)

Если положительных или отрицательных _j`` не существует, то соответствующим концом промежутка будет - или +.

При выходе за пределы этого промежутка в некотором столбце таблицы нарушится критерий оптимальности. Этот столбец следует выбрать в качестве разрешающего и далее преобразовать таблицу обычным способом. Из критериальной строки новой таблицы находят новый промежуток оптимальности. Эти действия повторяют до тех пор, пока не будет рассмотрен весь промежуток изменения параметра.

Если для начального значения L целевая функция задачи оказалась неограниченной, вначале находят бесконечный промежуток изменения L, для которого это имеет место (в соответствующем столбце нарушается критерий оптимальности):

(6)

Затем выходят за пределы этого луча и далее действуют обычным образом.

Если при поиске других промежутков оптимальности в выбранном столбце нет разрешающего элемента, то на соответствующем открытом промежутке L целевая функция задачи неограничена, и следует рассматривать оставшуюся часть числовой оси.

Например, решим симплекс-методом задачу о кондитерской фабрике. Для этого ее нужно вначале привести к канонической форме:

max (108 + 40L)х₁ + (140 + 20L)х₂

0 ,8х₁ + 0,5х₂ + х₃ = 800

0,2х₁ + 0,4х₂ + х₄ = 600

0,01х₁+0,1х₂ + х₅ = 120

х_1-5 0

L[0; +∞]

В этой задаче дополнительные переменные х₃, х₄ и х₅ обозначают неизрасходованные остатки ресурсов в тоннах (соответственно сахара, патоки и фруктового пюре).

Положим вначале L=0 и решим задачу для этого значения (при проверке критерия оптимальности пока не будем обращать внимание на коэффициент при L, поскольку это слагаемое будет равно нулю). Решение задачи представлено в таблице 4, разрешающие элементы выделены. При построении симплексной таблицы для этой задачи удобно строку коэффициентов целевой функции и критериальные строки представить в виде двух строк электронной таблицы, в первой из которых записывается слагаемое, не содержащее L, а в другой - коэффициент при L. Например, вместо ₁ = -108 – 140L в первой строке запишем -108, а во второй -140. Это делается для того, чтобы иметь возможность вычислять с помощью электронной таблицы (ведь выполнять арифметические действия с текстовыми выражениями программа не сможет).

Таблица 4 – Решение задачи симплекс-методом для L=0

				108	140	0	0	0
			L*	40	20	0	0	0
N	xб	cб	B	x1	x2	x3	x4	x5
1	x3	0	800	0,8	0,5	1	0	0
2	x4	0	600	0,2	0,4	0	1	0
3	x5	0	120	0,01	0,1	0	0	1
m+1			0	-108	-140	0	0	0
m+1(L*)			0	-40	-20	0	0	0
N	xб	cб	B	x1	x2	x3	x4	x5
1	x3	0	200	0,75	0	1	0	-5
2	x4	0	120	0,16	0	0	1	-4
3	x2	140 + 20L	1200	0,1	1	0	0	10
m+1			168000	-94	0	0	0	1400
m+1(L*)			24000	-38	0	0	0	200
N	xб	cб	B	x1	x2	x3	x4	x5
1	x1	108 + 40L	266,67	1	0	1,3333	0	-6,6667
2	x4	0	77,333	0	0	-0,2133	1	-2,9333
3	x2	140 + 20L	1173,3	0	1	-0,1333	0	10,667
m+1			19306,7	0	0	125,33	0	773,33
m+1(L*)			34133,3	0	0	50,667	0	-53,333

Из таблицы видно, что решением задачи будет Х^*=(266,7; 1173,3; 0; 77,333; 0), z^*=19306,7+34133,3L. Это решение останется верным до тех пор, пока все выражения в критериальной строке будут неотрицательными. Проверим это.

1 25,3 + 50,7L 0 L -2,5

773,3 - 53,3L 0 L 14,5

Итак, -2,5 L 14,5. Отметим, что для определения границ промежутка по модулю очень удобно воспользоваться Microsoft Excel. Предположим, например, что необходимые для расчетов числа находятся в диапазоне ячеек G20:I21 (таблица 5). Тогда достаточно в любую ячейку, например, в G22 ввести формулу «=G20/G21», которую затем скопировать по строке на соседние ячейки. Результат вычислений в электронной таблице представлен в таблице 5^* (он округлен с большей точностью: 2,5  2,4737).

Таблица 5 – Вычисление границ промежутка

	G	H	I
20	125,33	0	773,33
21	50,667	0	-53,333
22	2,4737	#ДЕЛ/0!	-14,5

Теперь следует выйти за пределы найденного промежутка. Поскольку отрицательные значения параметра в этой задаче нас не интересуют, рассмотрим L>14,5. Тогда коэффициент ₅ = 773,3 - 53,3L станет отрицательным, т.е. в столбце при х₅ нарушится критерий оптимальности. Преобразуем таблицу по этому столбцу (результат приведен в таблице 6).

Таблица 6 – Решение задачи симплекс-методом для L>14,5

N	xб	cб	B	x1	x2	x3	x4	x5
1	x1	108 + 40L	1000	1	0,625	1,25	0	0
2	x4	0	400	0	0,275	-0,25	1	0
3	х5	0	110	0	0,09375	-0,0125	0	1
m+1			108000	0	-72,5	135	0	0
m+1(L*)			40000	0	5	50	0	0

Из таблицы видно, что решением задачи будет Х^*=(1000; 0; 0; 400; 110), z^*=108000+40000L.

Найдем промежуток времени, для которого это решение останется верным.

1 35L -72,5 0 L 14,5

135 + 50 L 0 L -2,7

Итак, 14,5 L +.

Найденное решение снова представим в виде таблицы (таблица 6). Она отличается от таблицы 2 только тем, что теперь получена дополнительная информация о неизрасходованных ресурсах.

Таблица 6 – Результат решения задачи о кондитерской фабрике симплекс-методом

Время, месяцы (L)	Производство карамели		Неизрасходованный остаток			Выручка, тыс. руб. (z*)
	«Снежинка», т (х1*)	«Яблочная», т (х2*)	сахара, т (х3*)	патоки, т (х4*)	фруктового пюре, т (х5*)
[0; 14,5]	266,7	1173,3	0	77,3	0	193066,7 + 34133,3L
[14,5; +[	1000	0	0	400	110	108 000 + 40 000L

В силу экономической интерпретации данной задачи здесь бессмысленно рассматривать отрицательные значения L. Тем не менее, с теоретической точки зрения рассмотрим L < -2,5. Значение -2,5 было получено из таблицы 4: она являлась оптимальной при L [-2,5; 14,5]. При уменьшении параметра в этой таблице нарушится критерий оптимальности в столбце x₃. Если выбрать этот столбец в качестве разрешающего, то разрешающим элементом будет 1,33 (единственное положительное число в этом столбце). Этот коэффициент стоит в первой строке, где базисной переменной является х₁. Следовательно, необходимо преобразовать симплексную таблицу, введя в базис x₃ вместо х₁. Таким образом, в новой таблице базисными переменными будут x₃, x₄, x₂. Однако, нет необходимости осуществлять вычисления и строить новую таблицу. Дело в том, что таблица с таким составом базиса уже встречалась в ходе решения задачи – это предыдущая симплексная таблица в таблице 4. Из нее можно сразу же извлечь ответ: Х^* = (0; 1200; 200; 120; 0); z^* = 168000 + 24000L.

Это решение останется оптимальным при выполнении следующей системы:

- 94 - 38L 0 L -2,5

1400 + 200L 0 L -7

Осталось рассмотреть L < -7, т.е. преобразовать вторую симплексную таблицу в таблице 4 по последнему столбцу. При этом в базис войдет x₅ вместо x₂, и новый состав базиса будет x₃, x₄, x₅. Такой базис тоже уже встречался – в первой симплексной таблице. Тогда ответом будет Х^* = (0; 0; 800; 600; 120); z^* = 0.

Таким образом, если рассматривать не L  [0; +∞], а L  ]-∞; +∞], то ответ задачи следует представить в виде таблицы 7.

Таблица 7 – Результат решения задачи

Промежуток изменения L	Оптимальный план (Х*)	Оптимум (z*)
] -; -7]	(0; 0; 800; 600; 120)	0
[-7; -2,5]	(0; 1200; 200; 120; 0)	168000 + 24000L
[-2,5; 14,5]	(266,7; 1173,3; 0; 77,3; 0)	193066,7 + 34133,3L
[14,5; +[	(1000; 0; 0; 400; 110)	108 000 + 40 000L

Рассмотрим другой пример.

mах (6 + L)х₁ + (-3 – 5L)х₂

х ₁ - х₂ 2

х_1-2 0

L]-; +[

После приведения к канонической форме он примет вид:

mах (6 + L)х₁ + (-3 – 5L)х₂

х ₁ - х₂ + х₃ 2

х_1-3 0

В качестве базисной можно взять переменную х₁ либо х₃ (и там, и там столбец коэффициентов единичный). Возьмем х₁. Тогда симплексная таблица примет вид таблицы 8 (коэффициент ₂ вычислен по формуле (-1)*(6 + L) – (-3 – 5L) = 4L – 3; ₃ = 1*(6 + L) – 0 = 6 + L; значение целевой функции 2*(6 + L) = 12 + 2L).

Таблица 8 – Решение задачи симплекс-методом.

				6	-3	0
			L*	1	-5	0
N	xб	cб	B	x1	x2	x3
1	x1	6 + L	2	1	-1	1
m+1			12	0	-3	6
m+1(L*)			2	0	4	1

При L=0 критерий оптимальности нарушается в столбце x₂, но нет возможности ввести эту переменную в базис, так положительных коэффициентов в разрешающем столбце нет. Следовательно, целевая функция задачи не ограничена (задача не имеет решений). Определим, при каких значениях L это имеет место: 4L – 3 < 0  L < 0,75. Выйдем за пределы этого открытого промежутка. При L  0,75 ₂  0, т.е. в этом столбце критерий оптимальности не нарушен. Проверим выполнение этого критерия в остальных столбцах, а именно, для ₃: 6 + L  0  L  -6.

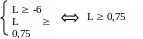
Следовательно, при L  0,75 полученная таблица оптимальна. Ответ можно представить в виде таблицы 9.

Таблица 9 – Результат решения задачи

Промежуток изменения L	Оптимальный план (Х*)	Оптимум (z*)
]-; 0,75[	Целевая функция не ограничена.
[0,75; + [	(2; 0; 0)	12 + 2L

Следует обратить внимание, что первый промежуток является открытым с обеих сторон. Граничное значение L = 0,75 здесь нельзя включать в оба промежутка, так как задача не может быть одновременно разрешимой и неразрешимой.