8. Вещественные квадратичные формы

Пусть V – пространство над - квадратичная форма на V. Тогда в V существует базис, в котором q(x) имеет нормальный вид где - не зависит от выбора базиса.

Теорема. (закон инерции) Число положительных и отрицательных коэффициентов в нормальном виде квадратичной формы не зависит от выбора базиса (т.е. s и r-s всегда одни и те же).

Пусть (в базисе ) (в базисе ). Предположим, что t < s. Обозначим Тогда Пусть Т.к. то где Аналогично, q(a)  0 т.к. Противоречие. Следовательно, t не может быть меньше s и наоборот. 

Опр. Если то s – положительный индекс инерции, а число (r – s) – отрицательный индекс инерции q.

Опр. Квадратичные формы p(x) и q(x) эквивалентны, если существует невырожденная матрица A, такая, что , где P и Q – матрицы p и q.

Следствие. Формы p(x) и q(x) эквивалентны  положительные и отрицательные индексы инерции совпадают.

 1)  Приведем к нормальному виду.

2)  аналогично. 

9. Теорема Якоби.

Пусть - матрица квадратичной формы f. Главные миноры .

Лемма. Ядро невырожденной симметрической БФ равно нулю.

 Пусть весь вектор матрица f в . Тогда где Но если Z – вектор-столбец, для которого то Z = 0. Следовательно, Но 

Теорема (Якоби). Пусть q – вещественная квадратичная форма с матрицей F, и Тогда  базис V, в котором q имеет вид где

Индукция по n.

1) Положим Тогда

2) n > 1. Обозначим Пусть f на U имеет матрицу По предположению индукции  базис в котором

Рассмотрим базис пространства V. Пусть Тогда - система из (n-1) линейных уравнений с n неизвестными   ненулевое решение Если то Но - ограничение f на U – невырожденная БФ, а - невырожденная квадратичная форма  (по лемме) на U. Условие u – решение системы означает, что -противоречие. Следовательно, Это значит, что -базис V, в котором f имеет матрицу 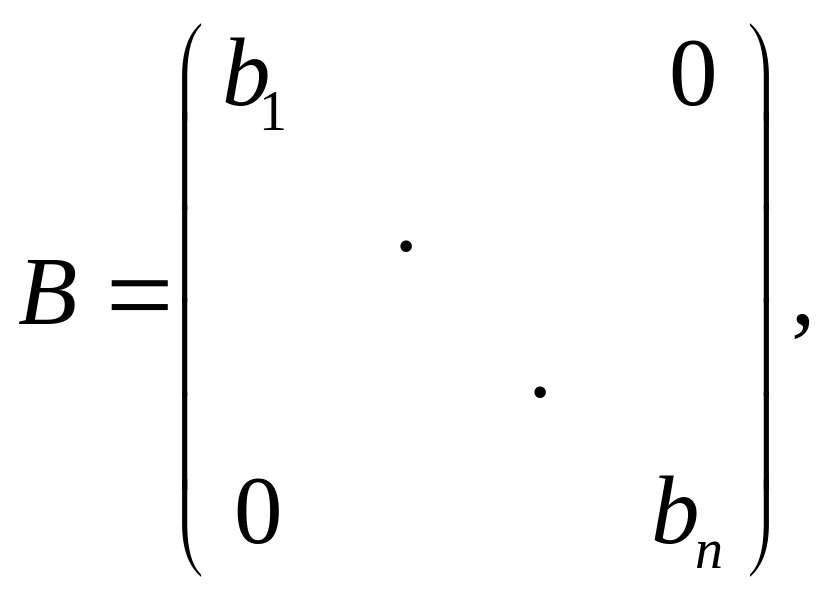причем

Пусть C – матрица перехода  тогда где Отсюда Но Положим Тогда и 

10. Положительно определенные квадратичные формы.

Опр. q – положительно определена на V, если

Канонический вид:

Нормальный вид:

Теорема (критерий Сильвестра). Квадратичная форма q с матрицей F положительно определена .

Предположим, что Тогда ограничение f – полярная БФ на имеет нетривиальное ядро (доказать!). Но тогда для некоторого - не положительно определенная. Следовательно, все . Теперь все следует из теоремы Якоби. 

Опр. Симметричная БФ называется положительно определенной, если - положительно определенная квадратичная форма.

11. Канонический вид кососимметричной бф

Пусть - кососимметричная БФ на V и

Замечание. Кососимметричная (или симметричная) БФ f невырождена (для фиксированного ).

Лемма. Пусть Тогда для любого подпространства такого, что ограничение f на невырождено.

Если для некоторого то (т.к. где .

Т.к. 

05.03.05

Теорема. Пусть – векторное пространство с невырожденной кососимметричной формой (билинейной). Тогда и существует разложение где , при . Кроме того, ограничение на имеет в некотором базисе матрицу .

Проведем индукцию по . - это противоречит невырожденности. Пусть .

Берем произвольный из . Тогда и т.к. то такой что . При этом и линейно независимы. Можно выбрать так, что и для все доказано.

Пусть теперь . Выберем любой из . Т.к. то такой что и , линейно независимы.

Обозначим . Дополним до базиса : . Рассмотрим . Тогда – подпространство, более того – пространство решений однородной системы линейных уравнений:

Где – матрица в базисе

Т.к. невырождена, то строки линейно независимы ранг системы равен 2. Поэтому и . Если ограничение на пространство имеет ненулевое ядро , то , что противоречит невырожденности, а это значит, что ограничение на – невырожденная кососимметричная билинейная функция

По индукции и все имеют требуемые базисы

Следствие. Для любой кососимметрической билинейной формы на пространстве существует базис, в котором она имеет матрицу

Где количество блоков равно половине ранга .