Polarplot ([переменная, выражение,параметры переменной],опции);
Пример.
Построить график функции sin(3*r) при r=0..7 (рис. 4.6).
[> restart; with(plots):
Warning, the name changecoords has been redefined
[>polarplot([r, sin(3*r),r=0..7],color=black,
thickness=3);
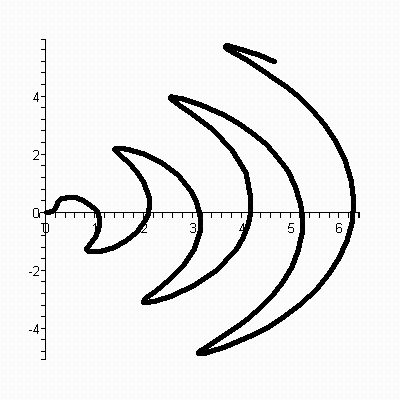
Рис. 4.6. График функции, построенный в полярной системе координат
В графическом пакете plot есть команда для построения графика по координатам точек, для этого нужно ввести координаты точек командой
data_list:=[[x1,y1],…,[xn,yn]];
а затем выполнить команду
Pointplot(data_list,опции);
Пример.
Построить график по координатам точек [2,4],[-4,4],[-2,3],[-1,4], [0,5] (рис. 4.7).
[> restart;
[> with(plots):
Warning, the name changecoords has been redefined
[> data_list:=[[2,4],[-4,4],[-2,3],[-1,4], [0,5]];
[>pointplot(data_list,style=line,color=black, thickness=3);
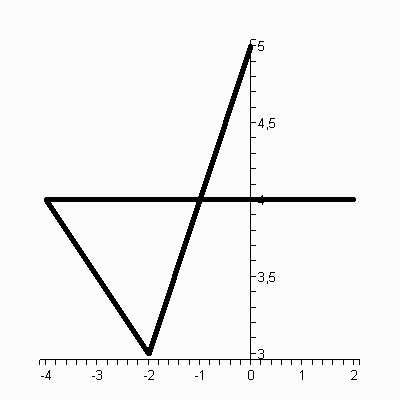
Рис. 4.7. График, построенный по координатам точек
Формат команды построения графиков в координат:
Sphereplot ((выражение), параметры_, параметры_, опции);
или
Sphereplot ([r_выражение, _выражение, _выражение], параметр_1, параметр_2, опции);
Пример.
Построить график функции в сферической системе координат (4/3)^theta*sin(phi), при theta=-1..2*Pi, phi=0..2*Pi (рис. 4.8).
[> restart;
[> with(plots):
Warning, the name changecoords has been redefined
[> sphereplot ((4/3)^theta*sin(phi),theta=-1..2*Pi, phi=0..2*Pi);
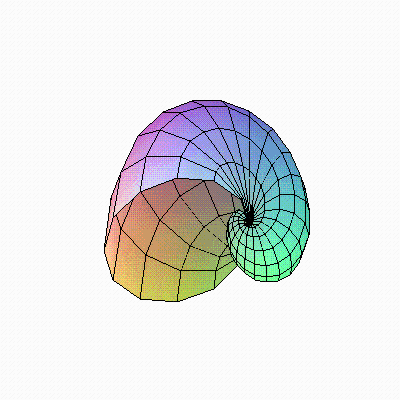
Рис. 4.8. График функции, построенный в сферической системе координат
4.1.2. Трехмерная графика
Команды трехмерной графики аналогичны командам двумерной графики и имеют окончания “3d”. Причем число параметров, как правило, больше на единицу, а точки определяются тремя координатами. Общий вид команды:
plot3d ({выражение_1, выражение_2,…}, переменная_1=а..b, переменная_2=c..d, опции);
Опции этой команды совпадают с параметрами построения двумерной графики. Кроме того, к специфическим опциям пакета plot3d следует отнести:
light=[x1,y1,c1,c2,c3] – задание подсветки поверхности, создаваемой источником света из точки со сферическими координатами x1, y1, цвет которой задается долями красного (с1), зеленого (с2), синего (с3) цветов из интервала [0,1];
style – задает стиль рисунка;
POINT – точки;
LINE – линии;
HIDDEN – сетка с удалением невидимых линий;
PATCH – заполнитель;
WIREАFRAME – сетка с выводом невидимых линий;
CONTOUR – линии уровня;
PATCHCONTOUR – заполнитель и линии уровня.
Параметр shading – задает опцию интенсивности заполнения, NONE – без раскраски.
Данная команда позволяет выводить на одном рисунке несколько поверхностей, задаваемые однотипными Maple выражениями, которые зависят от двух переменных переменная_1[а,b], переменная _2[c,d]. Вид рисунка можно менять при помощи опций.
Пример.
Построить поверхности функций xsin(2y)+ycos(3x), sqrt(x^2+y^2)-10, при x=-Pi..Pi, y=-Pi/2..Pi/2 (рис. 4.9).
[> restart;
[>plot3d({x*sin(2*y)+y*cos(3*x), sqrt(x^2+y^2)-10}, x=-Pi..Pi, y=-Pi/2..Pi/2, grid=[20,20],title="2 poverhnosti", axes=FRAMED, orientation=[20,60], color=x+y);
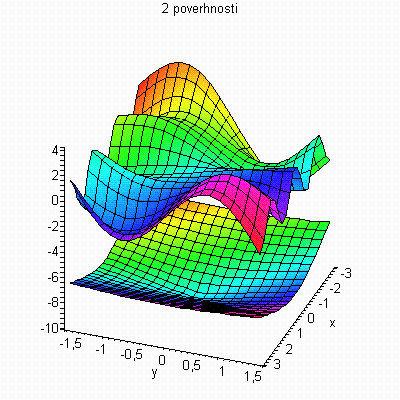
Рис. 4.9. Поверхности трехмерных функций
Если поверхность задана параметрически: x=x(u,v), y=y(u,v), z=z(u,v), построение графика задается командой
plot3d([x(u,v), y(u,v), z(u,v)],u=u1..u2, v=v1..v2);
В случае если поверхность задана неявно F(x,y,z)=0, то построение поверхности осуществляется с помощью следующей команды:
implicitplot3d(F(x,y,z)=0, x=x1..x2, y=y1..y2, z=z1..z2);
Кроме того, в пакете plot имеется команда spacecurve для построения пространственной кривой, заданной параметрически. Даная команда имеет следующую структуру:
spacecurve([x(t),y(t),z(t)],t=t1..t2);
Пример.
Построить поверхности функций, заданных параметрически x^2-y^2+z^2=4 при x=-10..10, y=-10..10, z=-10..10 (рис. 4.10, а).
[> restart;
[> with(plots):
Warning, the name changecoords has been redefined
[> implicitplot3d(x^2-y^2+z^2=4, x=-10..10, y=-10..10, z=-10..10, scaling=CONSTRAINED);
Если уменьшить границы просмотра графика ( с x=-10..10, y=-10..10, z=-10..10 до x=-2..2, y=-2..2, z=-2..2), то это приведет к его сильному искажению (рис. 4.10, б).
[> restart;
[> with(plots):
Warning, the name changecoords has been redefined
[> implicitplot3d(x^2-y^2+z^2=4, x=-2..2, y=-2..2, z=-2..2, scaling=CONSTRAINED);
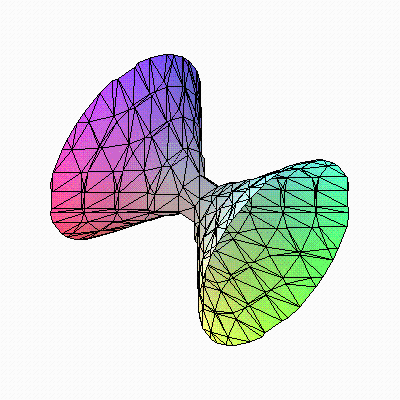
а)
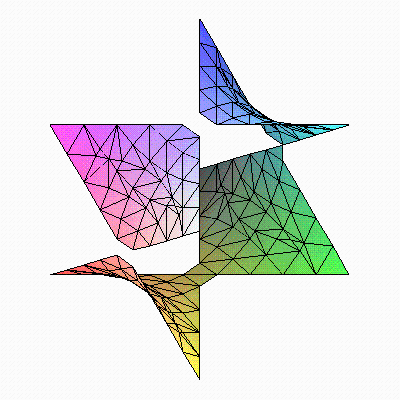
б)
Рис. 4.10. Поверхность функции, заданной параметрически
(а –x=-10..10, y=-10..10, z=-10..10;
б – x=-2..2, y=-2..2, z=-2..2)
Пример.
Построить трехмерное отображение изменения давления (Р=1,45,25,50,70,100,150,180 МПа) по уравнению регрессии, полученного экспериментально от трех переменных (х1, х2, х3).
Р=5.47-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+ +5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+ +5.02*x3^2.
Чтобы получить уравнения для построения трехмерного отображения нужно указанные в задании величины давления вычесть из первого члена уравнения, таким образом, получим восемь уравнений регрессии
[> restart;
[> with(plots):
Warning, the name changecoords has been redefined
[> implicitplot3d({4.47-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2,
-19.53-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+
5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2,
-39.53-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+
5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2,
-44.53-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+ 5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2,
-64.53-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+ 5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2,
-94.53-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+ 5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2,
-144.53-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+ 5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2,
-174.53-32.19*x1-22.09*x2-11.32*x3+0.625*x1*x2+ 5.63*x1*x3+0.625*x2*x3+38.26*x1^2+16.33*x2^2+5.02*x3^2 }, x1=-1..1, x2=-1..1 ,x3=-1..1, scaling=CONSTRAINED, orientation=[-56,49], axes=boxed);
На графике (рис. 4.11) отображено шесть поверхностей зависимости давления от трех факторов от трех переменных (х1, х2, х3) вместо восьми поверхностей, это объясняется тем, что давление больше 150 нецелесообразно использовать.
Рис. 4.11. Поверхности зависимости давления от трех факторов от трех переменных (х1, х2, х3).