12.1.2. Решение задачи
[> restart;
Используем пакет plot для вывода графиков на экран.
[> with(plots):
Warning, the name changecoords has been redefined
Вводим исходные данные.
Скорость энергоносителя на срезе разгонной трубки, м/с.
[> v1:=231.5;
Расстояние от среза разгонной трубки до плоскости встречи струй, м.
[> z0:=0.036;
Скорость энергоносителя от среза разгонной трубки до плоскости соударения струй изменяется по следующему закону:
[> v:=-v1*(z-z0)/z0;
Введем дифференциальное уровнение, описывающее процесс изменения скорости частиц и энергоносителя в помольной камере от среза разгонной трубки до области соударения встречных потоков:
[> ur:=u(z)*diff(u(z),z)=0.14*(v-u(z))*abs((v-u(z)));
Скорость энергоносителя на срезе разгонной трубки, м/с:
Построим графики, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,005 м (рис. 12.2); 0,003 м (рис. 12.3); 0,002 м (рис. 12.4); 0,001 м (рис. 12.5) при скорости энергоносителя на срезе разгонной трубке V0=231,5 м/с.
[> us:=u(0)=66.4;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027); re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
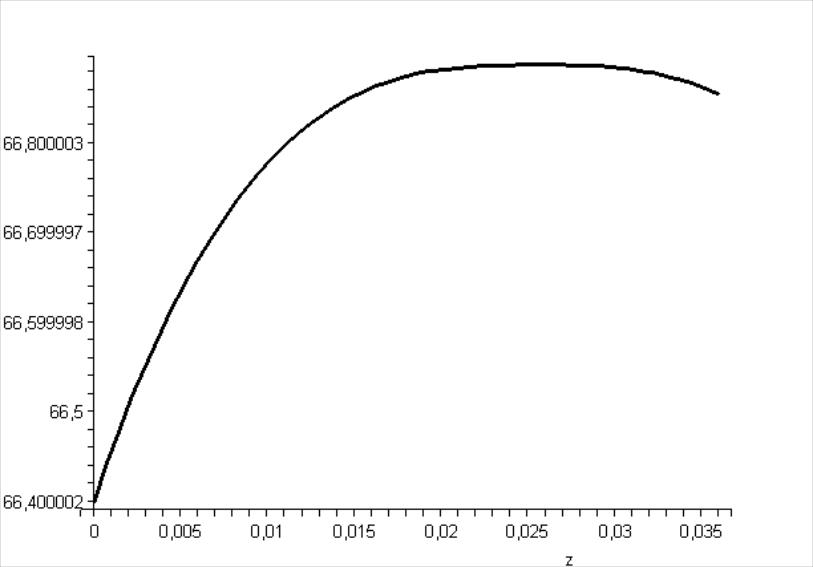
Рис. 12.2. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,005 м при V0=231,5 м/с
Частицы на начальном участке помольной камеры продолжают разгоняться энергоносителем, это происходит до того момента пока скорость энергоносителя выше скорости самих частиц.
[> us:=u(0)=80.6;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027); [> re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
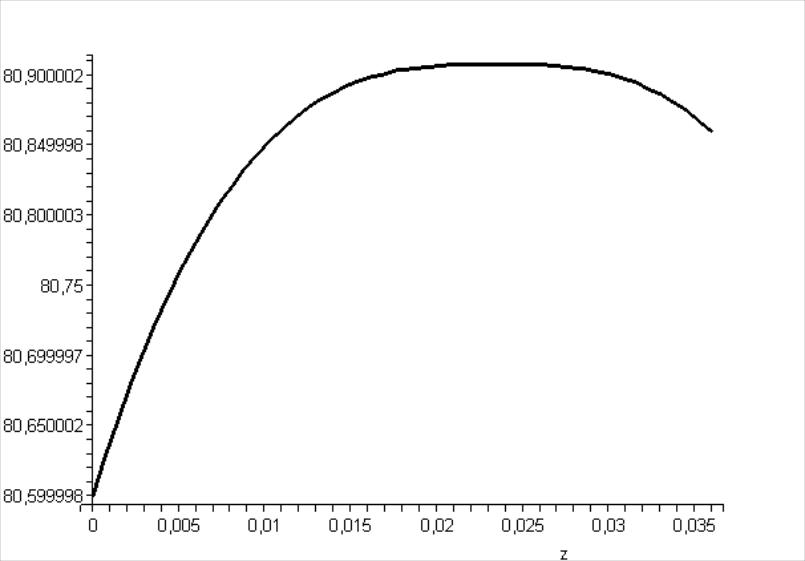
Рис. 12.3. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,003 м при V0=231,5 м/с
[> us:=u(0)=93.2;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027); re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
[> us:=u(0)=116.4;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027); re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
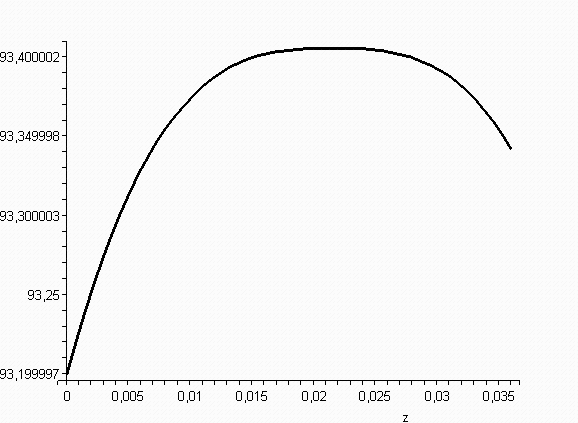
Рис. 12.4. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,002 м при V0=231,5 м/с
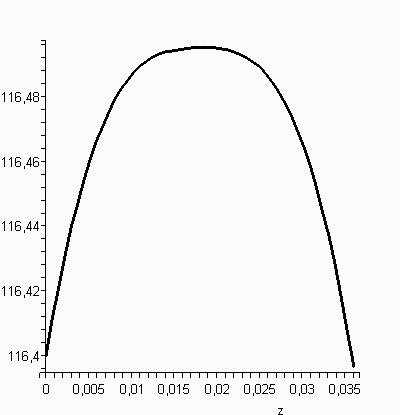
Рис. 12.5. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,001 м при V0=231,5 м/с
Построим графики, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,005 м (рис. 12.6); 0,00025 м (рис. 12.7) при скорости энергоносителя на срезе разгонной трубке V0=232,3 м/с.
[> us:=u(0)=232.1;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027);
[> re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
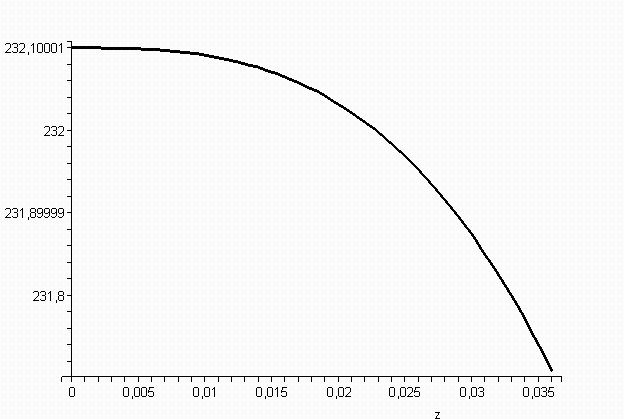
Рис. 12.6. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,005 м при V0=232,3 м/с
[> us:=u(0)=232.3;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027);
[> re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
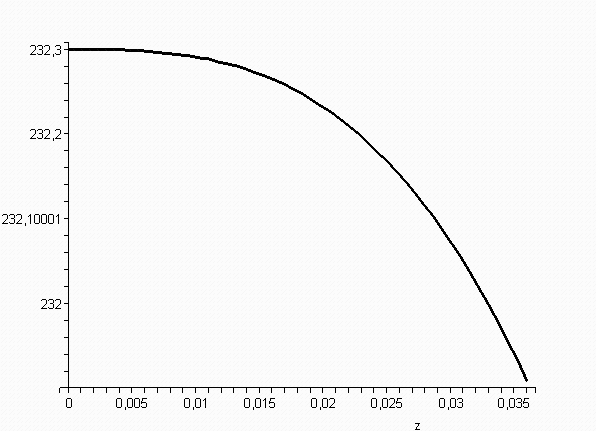
Рис. 12.7. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,00025 м при V0=232,3 м/с
Построим графики, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,005 м (рис. 12.8); 0,00025 м (рис. 12.9) при диапазоне скоростей энергоносителя на срезе разгонной трубке V0=293,5–297,3 м/с.
[> us:=u(0)=293.5;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027);
[> re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
[> us:=u(0)=297.3;
[> re:=dsolve({ur,us},u(z),numeric);
[> re(0.027);
[> re(0.036);
[> odeplot(re,[z,u(z)],0..0.036, color=black, thickness=2);
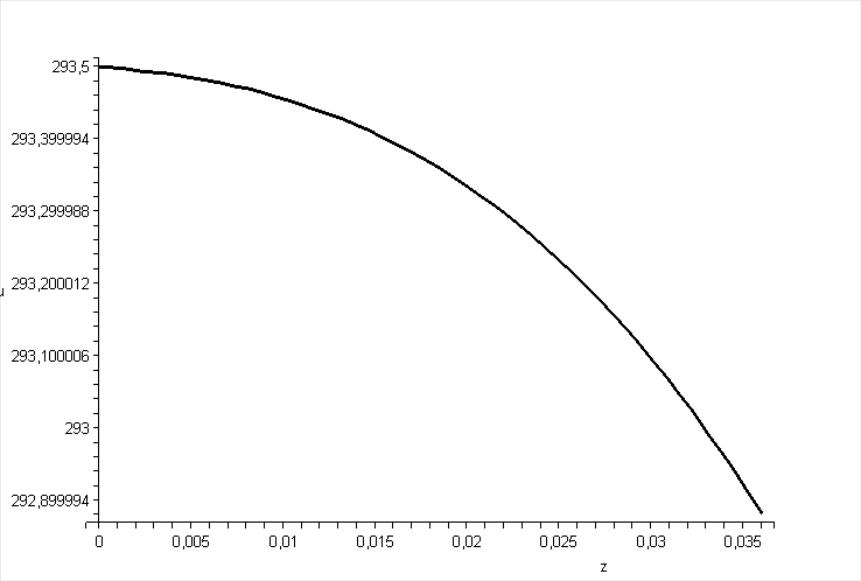
Рис. 12.8. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,005 м при V0=293,5 м/с
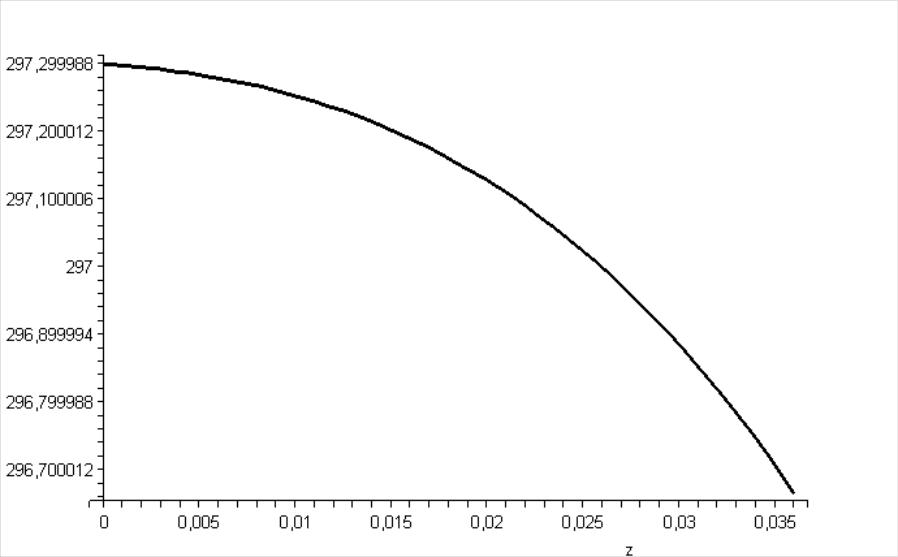
Рис. 12.9. График, зависимости изменения скорости частиц измельчаемого материала от среза разгонной трубки до встречи струй для частиц диаметром 0,005 м при V0=232,3 м/с
Расчитаем угол разлета материала. Введем исходные данные.
Скорость увлекаемой среды на срезе разгонной трубки.
[> v1:=0;
Коэффициент формы разгонной трубки.
[> k:=0.9;
Коэффициент зависящий от формы частиц увлекаемой среды.
[> psi1:=1;
Коэффициент учитывающий осесимметричность среды (для осесимметричной среды).
[> tgalpha:=0.222;
[> alpha:=arctan(tgalpha)*180/3.14;
Построим мультипликацию разлета частиц, где L изменяется от среза разгонной трубки до плоскости столкновения частиц 0…36 мм, =0…11.
[> for i from 0 by 1 to 11 do a[i]:=animate(cylinderplot, [L*tan(i*Pi/180)+0.009, theta=0..2*Pi, L=0..A],A=0..0.036); end do: for i from 1 by 1 to 5 do b[i]:=animate(cylinderplot, [i*0.009/5, theta=0..2*Pi, L=0..A], A=0..0.036); end do: display ({a[1], a[3], a[5], a[7], a[9], a[11], b[1], b[2], b[4], b[5]}, style=point);
Приведем графические структуры, отображающие изменение разлета частиц, где L изменяется с шагом 6 мм (рис. 12.10).
Выводы:
1. Практически все частицы, независимо от их размеров на входе помольной камеры продолжают разгоняться энергоносителем, происходит это до того момента пока скорость энергоносителя выше скорости самих частиц. После чего наиболее крупные из них (dэ=3..5мм), за счет большей инерции при полете к области взаимодействия встречных потоков, обладают практичсеки максимальной скоростью. А скорость мелких частиц (dэ=0,25..1 мм) начинает снижаться и в серединной плоскости помольной камерыдаже меньше, чем на выходе из разгонной трубке
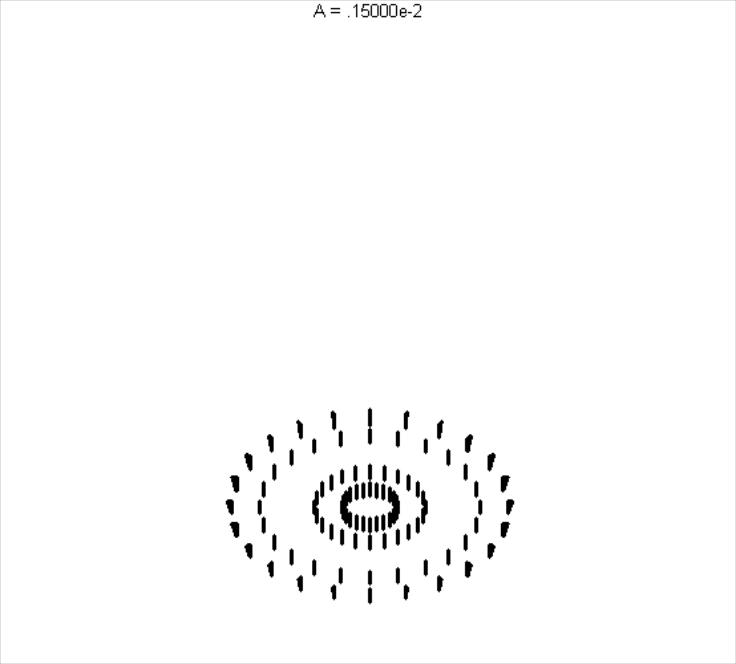
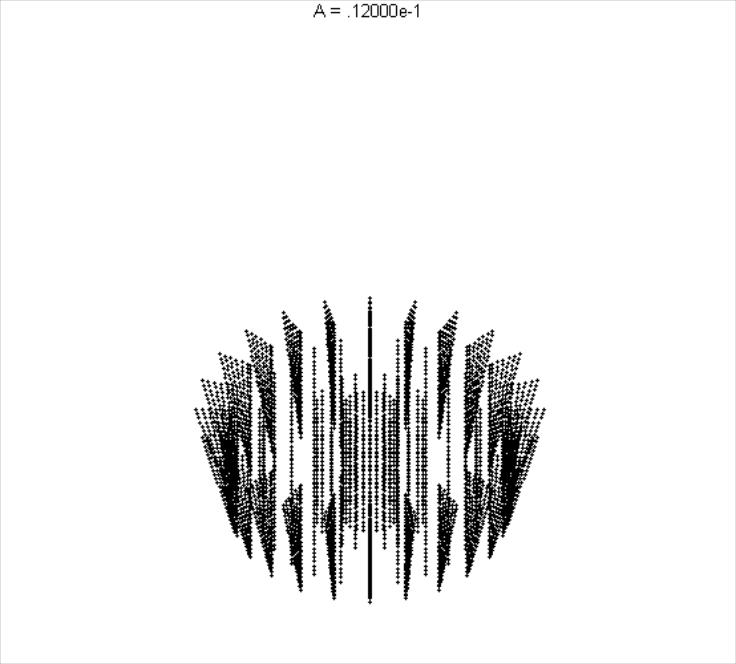
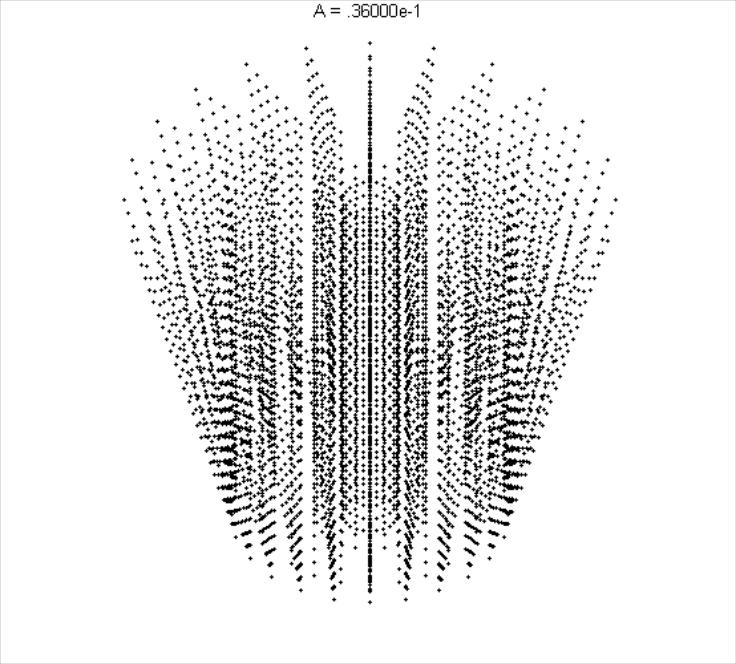
Рис. 12.10. Графические структуры, отображающие изменение разлета частиц с шагом 6 мм
2. Изменения скорости частиц при разных начальних скоростях энергоносителя на срезе разгонной трубки имеет одинаковый характер. Однако при более высоких значениях (V0=276..295 м/с) наблюдается эффект торможения частиц материала, даже для более крупных частиц. Это объясняется тем, что такие значения скорости на выходе из разгонной трубки можно достичь лишь при истечении из сопел эжекторов со скоростью близкой к критической, что приводит к увеличению турбулентных завихрений в разгоняемом потоке, а при выходе его из разгонной трубке имеет место раскрытие и «срыв» струи, и как следствие снижение эффективности процесса измельчения, за счет торможения частиц.