Is assumed to be: RealRange(Open(-1),3)

Согласно отмеченному выше вычисление интеграла с параметром , следует производить в таком порядке:

[> assume(a>0);

[>Int(exp(-a*x),x=0..+infinity)=int(exp(-a*x), x=0..+infinity);

Пример.

Найти определенный интеграл , при условии a > 0, b > 0.

[> assume (a>0); assume (b>0);

[>Int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*sin(x)^2)^2,x=0..Pi/2)=int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*sin(x)^2)^2,x=0..Pi/2);

[> q:=rhs(%);

[> simplify(%);

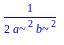
6.3. Основные методы интегрирования

В Maple имеется пакет student, который можно загрузить командой with(student). Данный пакет содержит набор подпрограмм, предназначенных для пошагового выполнения расчетов, приводящих к конечному результату. К таким командам относятся интегрирование по частям intparts и замена переменной changevar.

Как известно, формула интегрирования по частям имеет вид:

.

Если обозначить функцию, стоящую под интегралом f=u(x)v’(x), то параметры команды интегрирования по частям будут иметь вид: intparts(Int(f, x), u), где u(x) - функция, производную от которой предстоит вычислить по формуле интегрирования по частям.

Если в интеграле требуется сделать замену переменных x=g(t) или t=h(x), то параметры команды замены переменных будут иметь вид: changevar(h(x)=t,Int(f,x),t), где t  новая переменная.

Приведенные выше команды intparts и changevar не вычисляют окончательно интеграл, а лишь производят промежуточную подстановку. Для получения окончательного ответа, следует, после выполнения всех промежуточных вычислений ввести команду value(%); где % – обозначает выполнение команды от результата предыдущей строки.

Пример.

[> restart;

[> with(student):

[> intparts(Int(x^2*sin(x),x),x^2);

[> intparts(Int(-2*x*cos(x),x),x);

[> value(%);

Пример.

[> restart; with(student):

[>changevar(tan(x/2)=t,Int(1/(3*sin(x)+ 4*cos(x)), x),t);

[> expand(%);

[> simplify(%);

[> q:=value(%);

[> subs((t=tan(x/2)),q);

7. Дифференциальные уравнения

7.1. Аналитическое решение дифференциальных уравнений

7.1.1. Общее решение дифференциальных уравнений

Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение; var – неизвестная функция; options – параметры. С помощью параметров можно задавать метод решения задачи, по умолчанию ищется аналитическое решение: type=exact. При вводе дифференциального уравнения для обозначения производной нужно использовать команду прямого действия diff. Дифференциальное уравнение y''+y=x в среде Maple записывается в виде:

diff(y(x),x$2)+y(x)=x;

Общее решение дифференциального уравнения, которое, как известно, зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2 и т.д.

Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решение соответствующего однородного дифференциального уравнения), и слагаемые без произвольных постоянных (это частное решение этого же неоднородного дифференциального уравнения).

Команда dsolve выводит решение дифференциального уравнения в невычисляемом формате. Для того чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%).

Пример.

Найти общее решение дифференциального уравнения y'+y/x=e^x.

[> restart;

[> de:=diff(y(x),x)+y(x)/x=exp(x);

[> dsolve(de,y(x) );

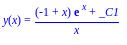
При записи решения дифференциального уравнения в Maple в строке вывода произвольная постоянная обозначена как _С1.

Пример.

Найти общее решение дифференциального уравнения второго порядка y''2y'+y=sinx+e^x.

[> restart;

[> eq:=diff(y(x),x$2)-2*diff(y(x),x)+y(x)

=sin(x)+exp(-x);

eq:=

[> dsolve(eq,y(x));

Так как исходное уравнение было второго порядка, то полученное решение содержит две произвольные константы, которые в Maple обычно обознаются как _С1 и _С2. Первые два слагаемых представляют собой общее решение соответствующего однородного дифференциального уравнения, а вторые два – частное решение неоднородного дифференциального уравнения.

Пример.

Найти общее решение дифференциального уравнения второго порядка y''+k²y=sin(qx) в двух случаях: qk и q=k (резонанс).

[> restart;de:=diff(y(x),x$2)+k^2*y(x)=sin(q*x);

de:=

[> dsolve(de,y(x));

Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q=k.

[> q:=k: dsolve(de,y(x));

Замечание: в обоих случаях частное решение неоднородного уравнения и общее решение, содержащее произвольные постоянные, выводятся отдельными слагаемыми.