Знф влечет 2нф влечет 1нф.

По этой причине, для того чтобы привести таблицы ко второй и третьей нормальным формам, достаточно пользоваться критерием третьей нормаль­ной формы. Если мы проверим, что каждый детерминант в таблице является ключом этой таблицы - критерий третьей нормальной формы - то все таб­лицы будут удовлетворять первой, второй и третьей нормальным формам. Это значительно упрощает процесс нормализации, поскольку нам нужно проверять только один критерий.

Наша версия третьей нормальной формы часто называется нормальной формой Бойса-Кодда (НФБК). Критерий третьей нормальной формы, ис­пользуемый многими авторами, логически несколько слабее критерия НФБК, которым мы пользуемся. Этот критерий утверждает, что таблица удовлетворяет ЗНФ, если в ней нет транзитивных зависимостей.

Транзитив­ная зависимость возникает, если неключевой атрибут функционально зави­сит от одного или более неключевых атрибутов.

Этот критерий не учитывает следующие два случая:

1. Неключевой атрибут зависит от ключевого атрибута, входящего в составной ключ (критерий нарушения 2НФ).

2. Ключевой атрибут, входящий в составной ключ, зависит от неключевого атрибута.

Нормальная форма Бойса-Кодда (НФБК). Любой детерминант, является ключом.

Транзитивная зависимость. Возникает, когда неключевой атрибут функцио­нально зависит от одного или более неключевых атрибутов.

НФБК учитывает оба эти случая. Таким образом, если таблица удовлетворяет НФБК, то она также удовлетворяет ЗНФ в смысле транзитивных зависимостей и 2НФ. Мы увидим, что наше определение ЗНФ упрощает процесс нормализации.

Задание 2.

Привести к 3НФ

A. EMPLOYEE (SS#, NAME, ADDRESS, PHONE, FATHER, SKILL)

ФЗ: ADDRESS -> PHONE

B. WORKER (W-ID, W-NAME, SPOUSE-SS#, SPOUSE-NAME)

ФЗ: SPOUSE-SS# -> SPOUSE-NAME

C. SALE (DATE, CUSTOMER, PRODUCT, VENDOR, VENDOR-CITY, SALESREP)

ФЗ: CUSTOMER -> SALESREP

D. EMPLOYEE (SS#, NAME, ADDRESS, PHONE, FATHER, FATHER-ADDRESS) ФЗ: FATHER -> FATHER-ADDRESS

E. WORKER (W-ID, W-NAME, SPOUSE-NAME, CHILDREN)

F. SALE (DATE, CUSTOMER, PRODUCT, VENDOR, VENDOR-CITY, SALESREP

ФЗ: VENDOR -> VENDOR-CITY, ФЗ: PRODUCT -> VENDOR

G. STUDENT (STUDENT-#, NAME, BLDG, FLOOR,-SENIOR-RESIDENT)

ФЗ: BLDG, FLOOR -> SENIOR-RESIDENT

Четвертая нормальная форма

Первая нормальная форма запрещает таблицам иметь неатомарные, или многозначные, атрибуты. Однако существует множество ситуаций моделиро­вания, требующих многозначных атрибутов. Например, в групповой системе медицинского страхования необходимо отслеживать нескольких людей, на­ходящихся на иждивении каждого работника. В колледже преподаватель факультета занят в нескольких комиссиях и отвечает за преподавание не­скольких предметов. Подобные примеры можно приводить довольно долго.

Как можно их смоделировать в реляционной базе данных, запрещающей многозначные атрибуты?

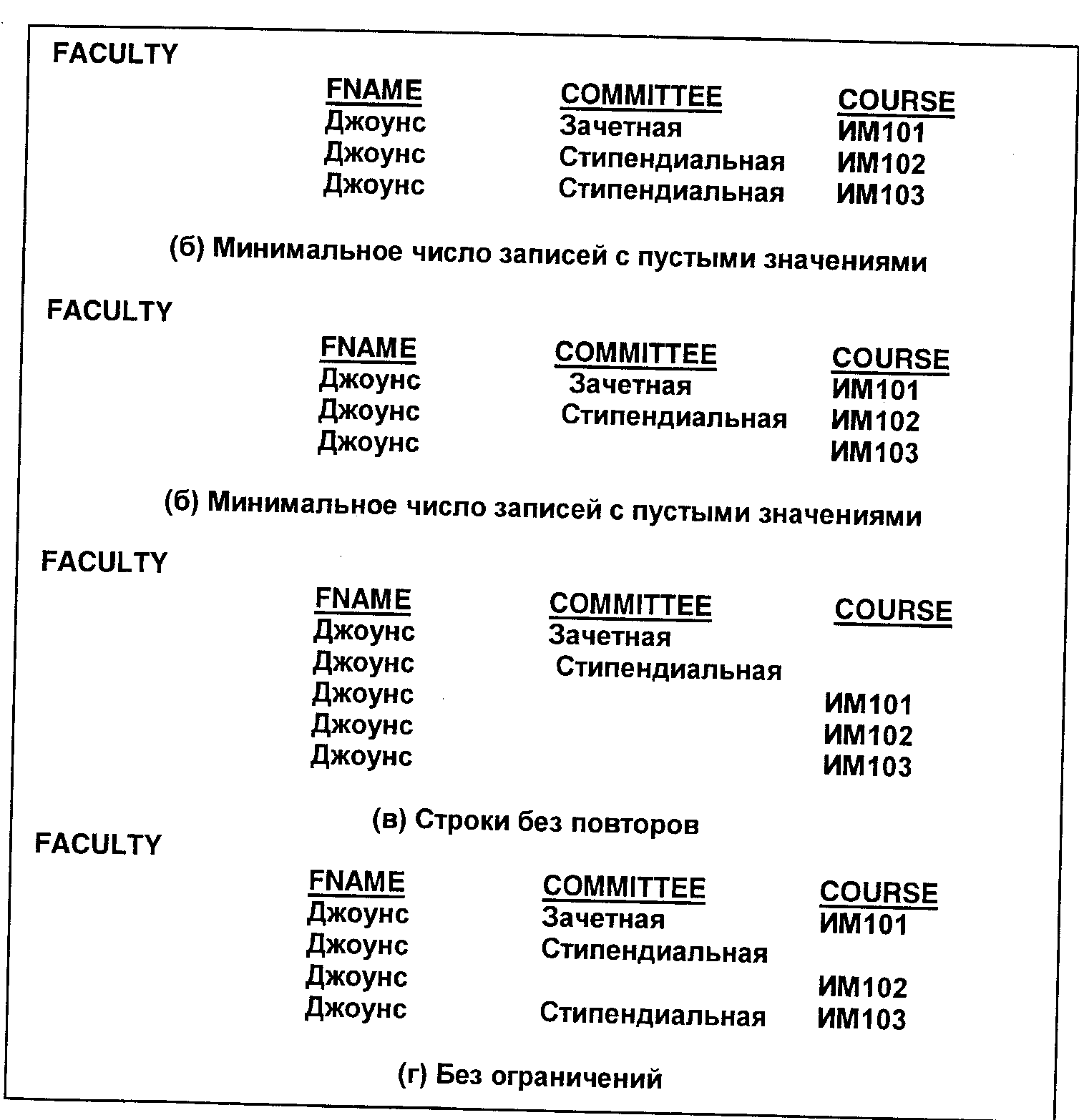
Рис. 9. Представление многозначных атрибутов в одной таблице

На рис. 9 представлены четыре возможных подхода к решению про­блемы участия преподавателей факультета в комиссиях и ведении предме­тов. Каждое решение имеет определенные недостатки. Все они требуют лиш­него места либо из-за наличия пустых значений, либо из-за необходимости вводить избыточные данные. Те из них, в которых есть пустые значения, нарушают категорную целостность, поскольку все атрибуты вместе состав­ляют ключ таблицы. Кроме того, предположим, что Джоунс назначен в ат­тестационную комиссию, и в базу данных требуется внести изменение. Нужно ли добавлять новую строку или исправлять старые данные? Наконец, не очевидно, что атрибуты COMMITTEE (КОМИССИЯ) и COURSE (ПРЕДМЕТ) не зависят друг от друга. Например, нельзя ли из рис. 9а сде­лать вывод, что зачетная комиссия каким-то образом зависит от предмета ИМ101?

Эти кажущиеся связи между независимыми атрибутами можно исклю­чить, потребовав, чтобы каждое значение атрибута сочеталось с каждым значением другого атрибута как минимум в одной строке. Это проиллюстри­ровано рис. 10, где и зачетная комиссия, и стипендиальная встречаются в строках с ИМ101, ИМ102 и ИМ103.

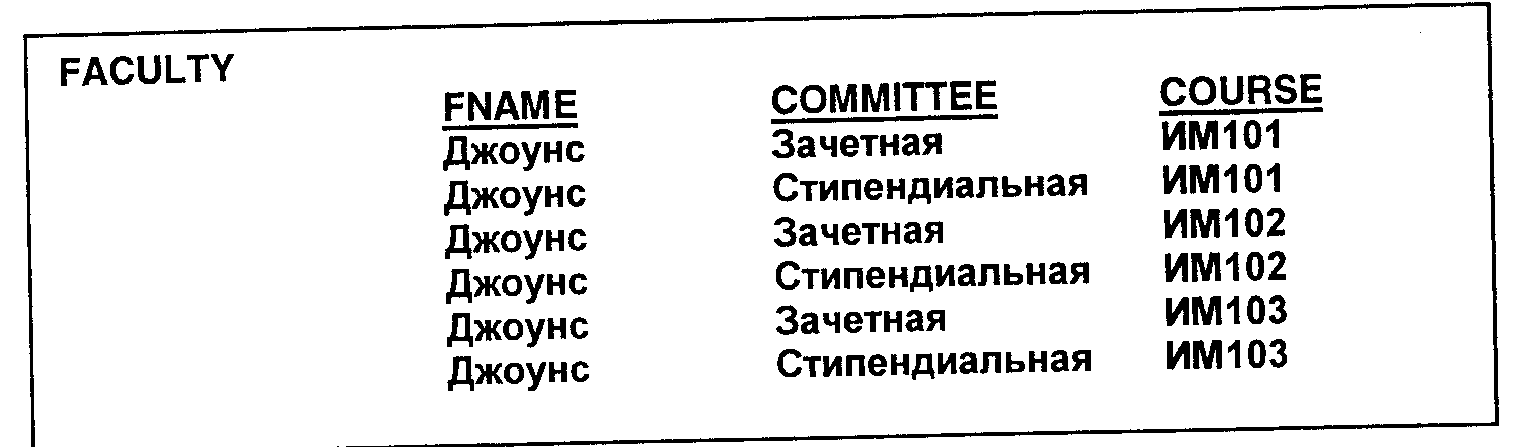
Рис. 10. Таблица FACULTY с многозначной зависимостью

Условие, обеспечивающее независимость атрибутов путем обязательного повторения значений, называется многозначной зависимостью (МЗЗ). МЗЗ является таким же ограничительным условием, как и ФЗ. Очевидно, что поскольку они требуют огромного числа повторений значений данных, важ­ный этап процесса нормализации состоит в избавлении от многозначных за­висимостей.

Многозначная зависимость (МЗЗ). Условие, обеспечивающее взаимную неза­висимость многозначных атрибутов.

Таблица имеет четвертую нормальную форму (4НФ), если она имеет ЗНФ и не содержит многозначных зависимостей. Поскольку проблема мно­гозначных зависимостей возникает в связи с многозначными атрибутами, то мы можем решить проблему, поместив каждый многозначный атрибут в свою собственную таблицу вместе с ключом, от которого атрибут зависит.

Рис. 11 иллюстрирует этот принцип. FNAME (ИМЯ-ПРЕПОДАВАТЕЛЯ) — ключ в некоторой другой таблице, идентифицирующей преподавателя, к ко­торому относится информация. Мы перечисляем комиссии, в которых участ­вует Джоунс, включив в таблицу по одной строке для каждой комиссии. Имя Джоунс повторяется в каждой строке. То же самое и для предметов, которые ведет Джоунс. Обе таблицы рис. 11 имеют четвертую нормальную форму (4НФ), так как все многозначные атрибуты (в нашем случае COMMITTEE и COURSE) были помещены в отдельные таблицы. Более того, такой подход преодолевает недостатки разных решений, представленных на рис. 9. Наконец, заметим, что ключом каждой нашей 4НФ-таблицы явля­ются оба атрибута таблицы. Таким образом, ключ таблицы FAC-COMM — (FNAME, COMMITTEE), а ключ таблицы FAG-COURSE — (FNAME, COURSE).

Четвертая нормальная форма (4НФ). Таблица, находящаяся в третьей нор­мальной форме и не содержащая многозначных зависимостей.

Рис. 11. Таблицы FAC-COMM и FAG-COURSE, обе в 4НФ