3.2. Позацентрово стиснуті елементи

До них належать колони та інші елементи, в яких поздовжні стискальні сили N діють з ексцентриситетом відносно поздовжньої осі, що проходить через центр ваги розглядуваного перерізу (рисунок 3.4,а), або в яких одночасно діють осьова поздовжня стискальна сила N і згинальний момент М (рисунок 3.4, б). І в тому, і в другому випадку розглядуваний переріз буде навантажений осьовою силою N і згинальним моментом М, дію якого можна змінити силою N, прикладеною з ексцентриситетом .

Залежно від величини ексцентриситету розрізняють два випадки позацентрового стиску: І — при великих ексцентри­ситетах, куди можна зарахувати і ,згин; II— при малих ексцентриситетах, зараховують і центральний (осьовий) стиск.

Отже, позацентровий стиск най­більш загальний і частий випадок на­пруженого і дефор­мованого стану еле­ментів конструкцій, а вигин і централь­ний стиск — його ок­ремі випадки.

При згині екс­центриситет прикла­дення поздовжньої сили такий великий, що практично мож­на знехтувати її вплив, а при так зва­ному центральному стискові можна зне­хтувати згинальний момент, бо ексцент­риситет малий.

Площу перерізу арматури, розміщену ближче до лінії дії поздовжньої сили прийнято позначати через , а віддале­ної — через (рисунок 3.5).

Фактичний ексцентриситет зручніше замінити роз­рахунковим тобто

ексцентриситетом поз­довжньої сили відносно центра ваги арматури А.

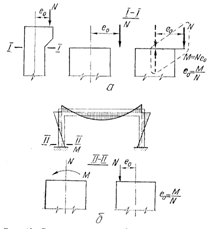
Рисунок 3.4 - Схема прикладення і сполучення розрахункових зусиль у перерізах позацентрово навантажених елементів

Перерізи елементів проектують звичайно розвинутими в пло­щині дії момента і симетричними

відносно обох осей (прямо­кутними, двотавровими, кільцевими) або несиметричними від­носно однієї з них, наприклад тавровими. В І і в IIвипадку позацентрового стиску поздовжню арматуру в поперечному пе­рерізі елементів можна розміщувати як симетрично, так і неси­метрично.

Таблиця 3.2 - Граничні значення l₀/h для обчислення с

Проектна марка бетону	l0/ri дорівнює або менше
	52	69	86	104	122
	l0/h дорівнює або менше
	15	20	25	30	35
«200»	0,55	0,40	0,30	0,20	0,10
«300»	0,50	0,35	0,25	0,15	-
«400»	0,40	0,30	0,20	0,10	-
«500»	0,35	0,25	0,15	0,05	-

Симетричне армування застосовують переважно тоді, коли в перерізі діють однакові або близькі за величиною, але різні за знаком згинальні моменти М (або М = е₀) і тоді, коли су­марний переріз робочої арматури ( ) перевищує не більш ніж на 5% економічне несиметричне армування.

Мінімальний переріз усієї поздовжньої робочої арматури в позацентрово стиснутих залізобетонних елементах повинен бути не менший, ніж величини, вказані в таблиці 2.2, і не слід призначатийого більшим за 3% від перерізу бетону. В противному разі треба додержувати додаткових конструктивних вимог

Критерієм, що визначає випадки позацентрового стиску є вже відома умова (2.4) достатньої міцності стиснутої зо­ни бутону: при має місце І випадок позацентрового стиску,а при —II випадок, де — коефіцієнт таблиця 6.

Висота стиснутої зони, як і в елементах, що зазнають згину, з подвійноюарматурою, повинна відповідати ще й умові (рис. 3.5,а), яка для прямокутних перерізів набирає вже відомого вигляду (2.16).

а – при великому ексцентриситеті; б – при малому ексцентриситеті прикладення повздовжньої сили

Рисунок 3.5 - Розрахунковий напружений стан у нормальних прямокутних перерізах позацентрово стиснутих елементів

Бетони високих марок якісно відрізняються від менш міцних.Високоміцні бетони більш чутливі до нерівномірності де­формацій за перерізом, бо зразу після того як напруги досягають межі утворення необоротних мікротріщин, швидко настає крихке руйнування таких бетонів. Здатність до перерозподілу напруг у бетонів високої міцності нижча, ніж у бетонів низьких і середніх марок ( < «400»). Тому граничне підношення прийнято за величину перемінну, що поступово знижується із збільшенням марки бетону (дивись таблицю 2.1).

При формули другого випадку позацентрового стиску, з одного боку, задовільно змикаються з формулами для центрального стиску, а з другого (оскільки ) —переходять у формули першого випадку.

Щоб така нерозривність зберігалась і при значеннях , треба ввести додаткові умови, що зроблено за пропозицією І.Л. Богаткіна, Б.Ф. Васильєва, О.О. Гвоздєвої і О.С. Залєсова: було введено поняття про граничний ексцентриситет і умову . Додатковий множник [А] у величини призмової міцності бетону при цент­ральному стиску дорівнює одиниці, а із збільшенням ексцентри­ситету лінійно зменшується.

Розглянемо, як дістають розрахункові і робочі формули для позацентрово стиснутих елементів з найбільш вживаних бетонів і марки «400» і менше.

Прямокутні перерізи. І випадок — великого ексцен­триситету — має місце, коли — при си­метричному армуванні, або коли —при несиметрич­ному.

При елемент розраховують як такий, що зазнає згину.

Розміри поперечних перерізів позацентрово стиснутих еле­ментів, як правило, відомі, бо їх вибирають, а потім ще пере­віряють під час статичного розрахунку. Тому їх розрахунок зво­диться до підбору перерізу поздовжньої арматури і . Для цього на підставі передумов, викладених у 1.5, і розглядаючи рисунок 3.5,а, записують два рівняння:

перше — сума моментів усіх сил відносно центра ваги ар­матури дорівнює нулю ( )

Звідки

(3.8)

друге— сума проекцій всіх сил на вісь елемента дорівнює нулю

( ):

,

звідки

. (3.9)

Робочі формули дістають з цих рівнянь залежно від способу армування елементів.

При симетричному армуванні переріз арматури і зна­ходять з рівняння (3.8)

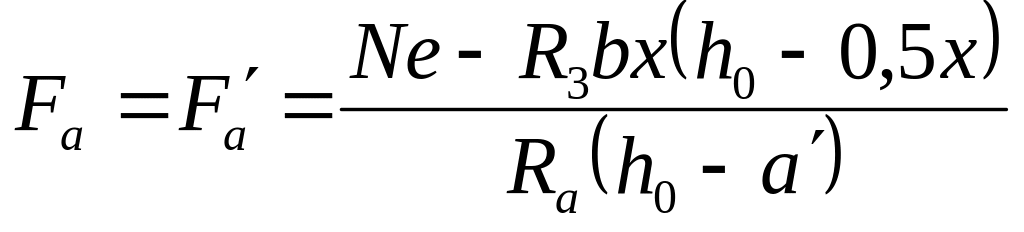, (3.10)

де при симетричному армуванні не тільки , а й .

До формули (3.10) входить висота стиснутої зони бетону х, яку знаходять з рівняння (3.9), вважаючи (оскільки армування симетричне)

(3.11)

При несиметричному армуванні може бути багато варіантів, серед яких слід вибирати такий, в якому сумарне значення і було б мінімальним.

З цією метою записують величини з рівняння (3.8) і з рівняння (3.5), потім знаходять мінімум їх суми, прирівнюючи першу похідну по х нулю

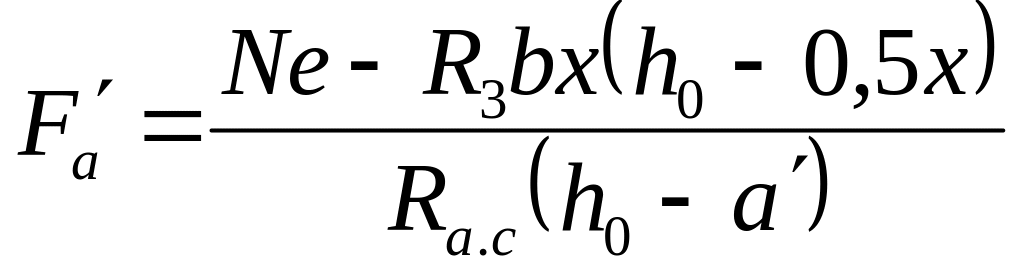, (3.12)

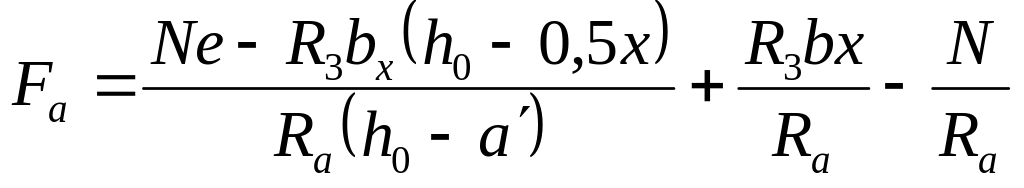, (3.13)

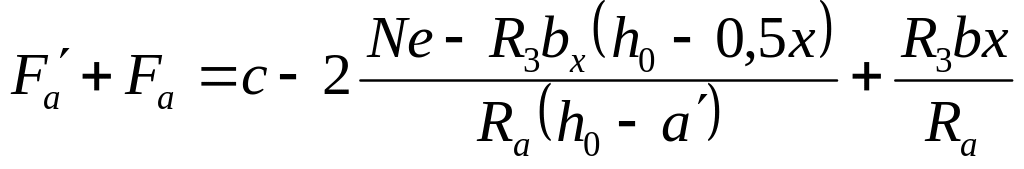
де сума членів ,які не містять змінної .

;

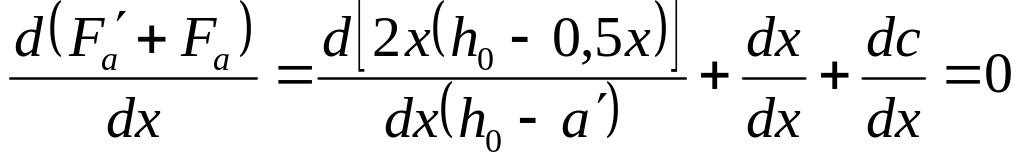
Прийнявши , дістанемо шукане відношення , при якому

( ) дорівнює мінімуму.

Помноживши другий доданок у чисельнику формули для на дістанемо

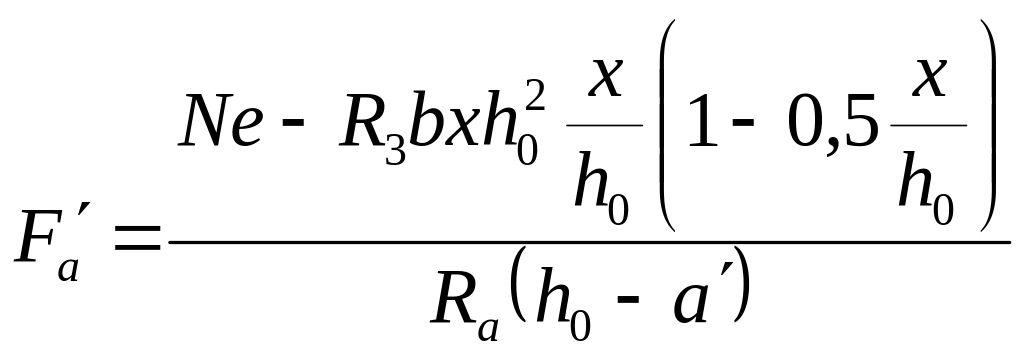
Підставивши в цю формулу числове значення дістаємо остаточно

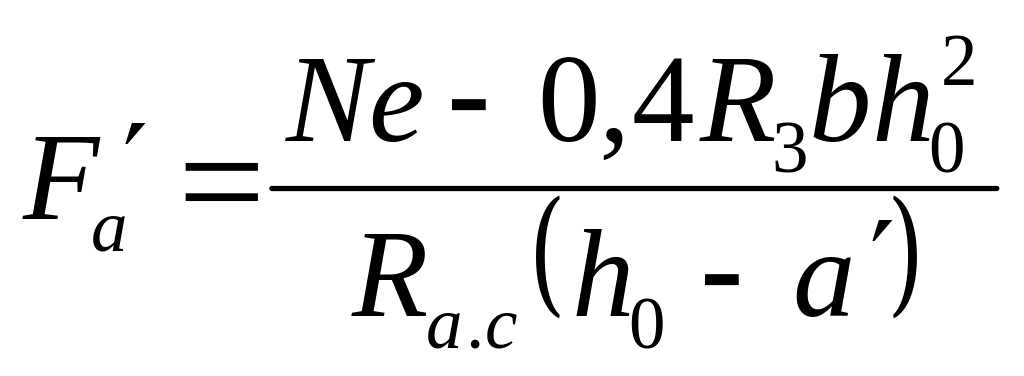. (3.14)

Зауважимо, що ця формула при цілком збігається з формулою (2.17) для визначення перерізу в елементах,що зазнають згину, з подвійною арматурою (дивись приклад 3).

Переріз арматури знаходять з рівняння (3.9) . Підставивши , дістанемо

, (3.15)

де знаходять за формулою (3.14).

IIвипадок — малогоексцентриситету — має міс­це при

(для ) і (для )

При малих ексцентриситетах арматура буде слабо стис­нута або слабо розтягнута (бо напруги в ній в тому і в дру­гому випадку ). Це вносить невизначеність у картину напруженого стану за перерізом елемента в стадії його руйну­вання. Для розв'язання цієї невизначеності потрібні були до­даткові експериментальні дані. В 1935 р. в результаті широких досліджень, здійснених М.С.Бориніанським та О.О.Гвоздєвим, такі дані було здобуто, причому прийнято, що при малих ексцентриситетах момент граничного зусилля, що сприймається стиснутим бетоном, відносно центра ваги арматури можна вважати незалежним від величини ексцентриситета і практично величиною сталою: N_бе_б =const.

А оскільки це так, то величину можна записати як для випадку центрального стиску

Замінюючи призмову міцність R_пр = 0,8R₃, оскільки і в II ви­падку позацентрового стиску деформації згину мають місце, дістанемо

Тепер можна скласти перше рівняння

звідки

. (3.16)

Другерівняння відносно центра ваги арматури складають так, щоб при несиметричному армуванні, коли і малих ексцентриситетах руйнування перерізу не поча­лося з слабшої, але дуже стиснутої (бо ексцентриситет малий) арматури

звідки

, (3.17)

де в першому доданку залишають R_пр замість оскільки ексцентриситети дуже малі.

При симетричному армуванні переріз арматури дістають з рівняння (3.16)

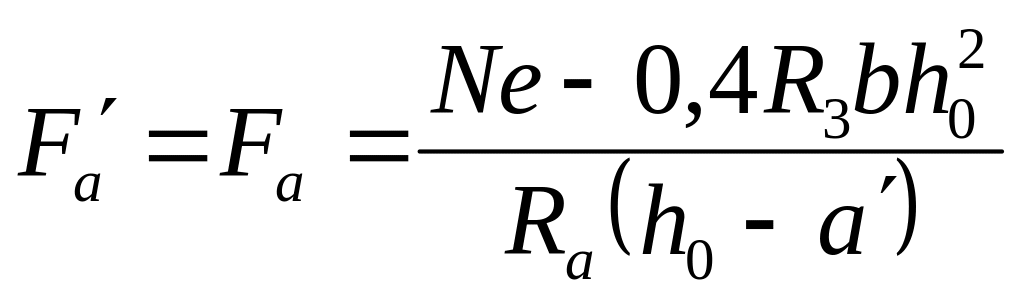. (3.18)

При несиметричному армуванні

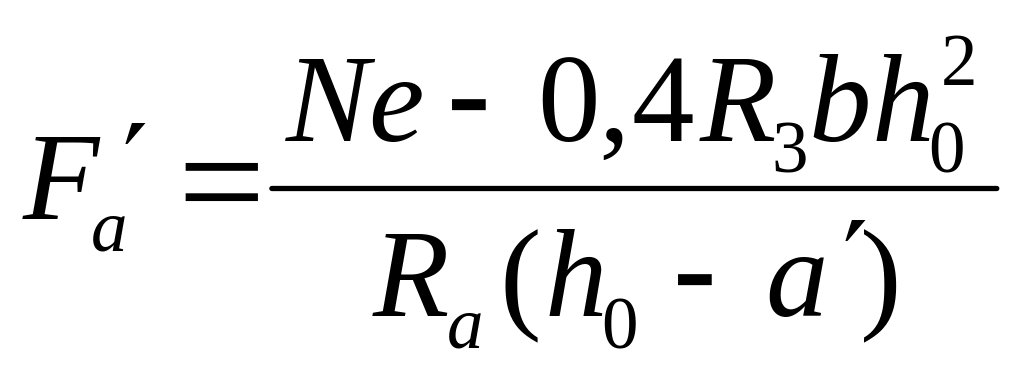, (3.19)

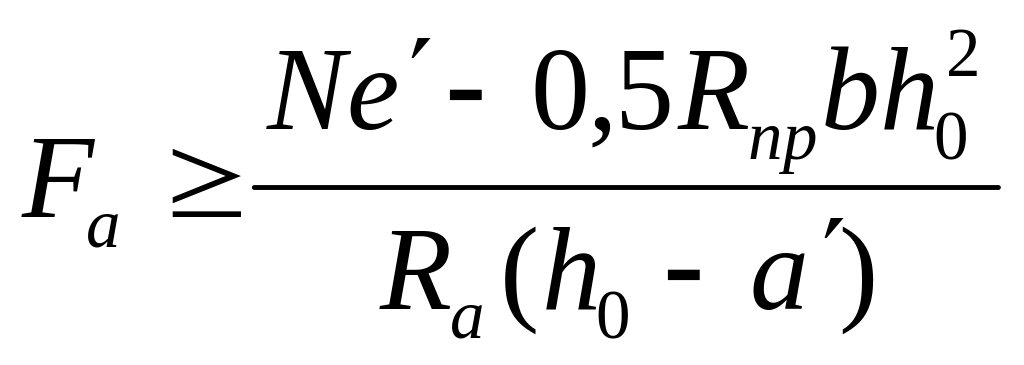, (3.20)

де або .

Прирівнявши для граничного випадку праві частини рівнянь (3.8) і (3.16), можна дістати критерій переходу великого ексцентриситета в малий або навпаки: , звідки, розв’язуючи квадратне рівняння, дістанемо граничну умову.

При цьому, тобто при малій висоті стиснутої зони х, має місце випадок — великого ексцентриситета, а при , тобто при великій висоті стиснутої зони, що поширюється і на переріз,— II випадок — малого ексцентриситета. Ці граничні умови і записані вище, коли розглядався кожний випадок позацентровості. Ті окремі випадки, коли переріз або дістаютьрівним нулю або від'ємним (оскільки у відповідних формулах числівники записані як різниця двох величин), розглядають прикладах розрахунків.

Контрольні питання

1. Що вважають центрально стискуючими елементами

2. Що відноситься до центрово-навантажених елементів

3. На чому ґрунтується розрахунок міцності центральностиснутих елементів

4. Як проводиться розрахунок при симетричному і несиметричному армуванні елемента