8 Оптимизация режима работы неоднородной электрической сети

8.1. Постановка задачи

Для неоднородной замкнутой электрической сети, рис.8, опре­де­лить условия размыкания контура на шинах подстанции Б для снижения потерь активной мощности в сети.

Рис.8. Схема неоднородной электрической сети

8.2. Основные соотношения

Ограничения и допущения:

• рассматривается единственный режим для заданных значений активной и реактивной мощности нагрузки;

• минимизируются только нагрузочные потери мощности в сети;

• ограничения на уровни напряжений в узлах отсутствуют.

Математическая формулировка задачи.

Формально имеем задачу нелинейного программирования: минимизировать f(x), x Î Eⁿ при m ограничениях в виде равенств h_j(x) = 0, j = 1,2,...,m и (p - m) ограничениях в виде неравенств g_j(x) ³ 0, j = m + 1, m + 2,...,p.

Целевой функцией f(x) в данной задаче является величина суммарных потери мощности DP_, включающие потери во всех элементах схемы сети (две ЛЭП и два трансформатора).

В данной задаче ограничения типа неравенств не являются определяющими, так как при допустимом исходном режиме изменение потокораспределения с целью снижения потерь в сети (при ее размыкании), как правило, не утяжеляет режим ни по нагрузке, ни по уровням напряжения.

Расчетная схема сети.

Расчетная схема сети приведена на рис. 9.

Рис. 9. Расчетная схема сети

Мощность нагрузки S_Н представим в виде суммы двух нагрузок S_Н = S_Н1 + S_Н2, распределенных между двумя секциями шин.

Представим каждый из четырех элементов электрической сети (две ЛЭП и два трансформатора) четырехполюсниками в А-форме, рис. 10.

Рис. 10. Расчетная схема сети при ее представлении в виде четырехполюсников

Коэффициенты четырехполюсника для ЛЭП определяются по формулам:

Для повышающего трансформатора:

Для понижающего трансформатора:

Здесь Z и Y – сопротивление и проводимость ЛЭП, Z_т и Y_μ – сопротивление и проводимость трансформатора.

В трансформаторах ветвь проводимости Y_ присоединена в схеме замещения со стороны питания, т. е. Y_1 на напряжении 110 кВ, а Y_2 на напряжении 220 кВ. Заметим, что для ЛЭП четырехполюсник является симметричным, а для трансформаторов – несимметричным. Для всех элементов сети четырехполюсники фактически являются трехполюсниками, т. е. потенциал одного полюса входа и выхода одинаковый и для трехфазной симметричной системы равен нулю и теоретически может быть соединен с общей гипотетической нейтралью системы N.

С учетом каскадного соединения Т-1 с Л-1 и Т-2 с Л-2 имеем эквивалентный четырехполюсник #1, рис. 11:

Рис. 11. Эквивалентная схема с четырехполюсниками

Целевая функция и ограничения.

В качестве независимых переменных примем нагрузку шин 1 (P₁ и Q₁) подстанции Б. Нагрузка шин 2 выражается при этом как P₂ = P_Н – P₁ и Q₂ = Q_Н – Q₁.

Целевая функция в данном случае может быть явно выражена через независимые переменные:

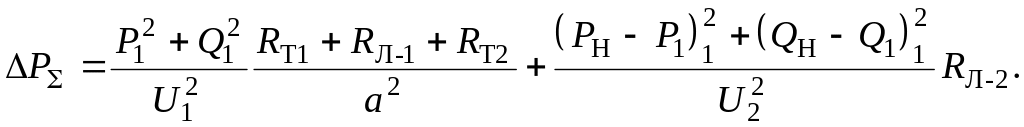
Условие экстремума запишется как:

Эти два уравнения и ограничения в виде равенств, записанные как УУН для шин 1 и 2 через коэффициенты четырехполюсников, образуют систему уравнений для решения задачи оптимизации. Кроме мощностей P₁ и Q₁ искомыми переменными являются модули и фазы напряжений шин 1 и 2: U₁, ₁, U₂ и ₂.