1. Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Числа a_ij називають елементами матриці,а запис m x n – розмірністю матриці. Рангом матриці називається найбільший з порядків її мінорів відмінних від 0.

2.Дії над матрицями:

• Сумою матриць A i B називається матриця С=А+В, будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В(тільки для матриць однакового розміру).

• Добутком матриці A на деяке число k називається така матриця С, кожен елемент якої cij одержується множенням відповідних елементів матриці А на k:cij=k*aij.

• Різниця матриць А і В визначається як сума м.А і м.В помноженої на -1.

• Добутком матриць С=А*В називається матриця, у якої елемент cij дорівнює сумі добутків елементів і-го рядка м.А на відповідні елементі j–го стовпця м.В.

3.Матриця А^-1 називається оберненою до м.А, якщо виконується наступна умова:

А * А^-1 =А^-1 * А=Е (тільки для квадратних матриць).Обернені матриці існують тільки для невироджених матриць .

4.

5.Вичерпну відповідь на запитання про існування розв’язку системи рівнянь дає теорема Кронекора-Капелі. Для того щоб система лінійних рівнянь була сумісною необхідно і достатньо, щоб ранг її основної матриці = рангу розширеної матриці, якщо ранг основної матриці = рангу розширеної матриці і = числу невідомих, то система має єдиний розв’язок. Якщо ранг основної матриці = рангу розширеної матриці, але менше числа невідомих, то система має безліч розв’язків.

6. Метод координат - спосіб визначати положення точки або тіла за допомогою чисел або інших символів (наприклад, положення шахових фігур на дошці визначається за допомогою чисел і літер). Числа (символи), що визначають положення точки (тіла) на прямий, площині, впросторі, на поверхні і так далі, називаються її координатами. Залежно від цілей і характеру дослідження вибирають різні системи координат. Положення точки на прямій визначається однією координатою х.

7. Прямокутна система координат на площині утворюється двома взаємно перпендикулярними осями координат X 'X і Y 'Y . Осі координат перетинаються в точці O , яка називається початком координат.

8. Ві́дстань між двома́ то́чками — довжина уявного відрізка, кінцями якого є ці точки. Найкоротший шлях, яким можна дістатися з однієї точки в іншу. Квадрат, відстані між двома точками дорівнює сумі квадратів різниць їх відповідних координат.

9. Нехай відрізок AB задано координатами його кінців A( x1,y1) і B(x2,y2) . Відомо,

що на цьому відрізку між точками A і B знаходиться точка M , яка ділить відрізок у

заданому відношенні L(лямбда) > 0 . У векторній формі указаний поділ має вигляд

AM/MB=L, де AM і MB – колінеарні вектори. Необхідно знайти координати точки M (x, y).

x=(x1+L*x2)/(1+L); y=(y1+L*y2)/(1+L)

1 0.

11. Рівняння F (x, y) = 0 називається рівнянням деякої лінії в заданій системі координат, якщо це рівняння задовольняють координати (х, у) будь-якої точки, що лежить на цій лінії, і не задовольняють координати жодної точки, що не лежить на цій лінії.

Нехай задано деяку пряму, знайдемо її рівняння.

Позначимо tg = k і назвемо цю величину кутовим коефіцієнтом прямої лінії. Тоді, враховуючи, що NM = y – b, BN = x, маємо рівняння прямої з кутовим коефіцієнтом:

у = kx + b.

Нехай деяка точка М1 (х1, у1) належить заданій прямій, тоді у1 = kx1 + b. Знайдемо з цього рівняння значення b і, підставивши його в рівняння прямої (2.14), дістанемо:

у – у1 = k (х – х1)

12.

13.

14.

15.

1 6. Колом називають множину усіх точок площини, відстані яких від заданої точки площини, що називається центром кола, є величина постійна і дорівнює радіусу кола.

1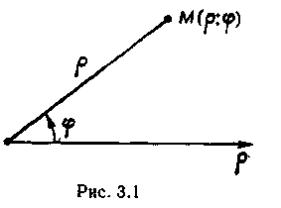 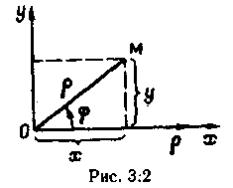7.Еліпсом називають множину усіх точко площини,сума відстаней яких від двох заданих точок цієї площини, які називаються фокусами є величина стала і більша за відстань між фокусами.

18.Із означення еліпса 2а>2с і b²=a²-c².

Оскільки канонічне рівняння еліпса містить тільки члени з парними степенями х і у, то еліпс симетричний відносно осей Ох і Оу, а також початку координат. Точку О(0,0) – називають центром еліпса. Еліпс перетинає осі координат в точках А1(-а,0), В1(0,b), А2(а,0), B2(0,-b). Ці точки називаються вершинами еліпса.

Величини А1А2=2а, В1В2=2b – називаються великою і малою осями еліпса відповідно. а і b – називаються великою и малою півосями еліпса. Весь еліпс вміщується в прямокутник зі сторонами 2а і 2b. Сторони прямокутника дотикаються до еліпса в його вершинах.

Якщо а=b, то рівняння еліпса має вигляд х²+у²=а².

Відстань F1F2=2c називається фокальною відстанню, F1(-c,0), F2(c,0).

Міра відхилення еліпса від кола характеризується величиною ε, яка називається ексцентриситетом еліпса і дорівнює ε=с/a.(0≤ε≤1).

Нехай М(х,у) – довільна точка еліпса, з фокусами F1 і F2. Відстань F1M=r1 і F2M=r2 – називаються фокальними радіусами еліпса. r1+r2=2a.

Прямі x=a/ε і x= -a/ε називаються директрисами еліпса. Відношення фокальних радіусів довільної точки еліпса до відстаней цієї точки від відповідних директрис є величина стала і дорівнює ексцентриситету еліпса(r1/d1=r2/d2=ε).

19.Гіперболою називаються множину усіх точок площини,модуль різниці відстаней яких від двох заданих точок цієї площини, що називаються фокусами є величина стала і меньше відстані між фокусами.

20.

21.Параболою називаються множину всіх точок площини, кожна з яких знаходиться на однаковій відстані від даної точки, яка називається фокусом і від даної прямої, що зветься директрисою и не проходить через фокус.

22.

Вектор – це величина,яка крім числового значення характеризується ще і напрямком.

Два вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих. Колінеарні вектори можуть буди напрямлені однаково або протилежно.

23.

24.Сума двох векторів а і b є вектор с напрямлений з початку вектора а в кінець вектора b, за умовою, що початок вектора b збігається з кінцем вектора а. Це правило додавання векторів називається правилом трикутника. Суму двох векторів можна побудувати за правилом паралелограма. а+ b є вектор с, який є діагоналлю паралелограма побудованого на векторах а і b, зведених до спільного початку, і яка виходить з нього.

Віднімання векторів визначається як дія обернена додаванню. Різницею а- b називається вектор с, який будучи доданий до вектора b дає вектор а.

Добутком вектора на число називається вектор (або , що має довжину , колінеарний векторові , має напрямок вектора , якщо і протилежний напрямок, якщо .

Властивості:

1.Комунікативність відносно додавання:

2.Асоціативність відносно додавання:

3.Асоціативність відносно множення на число:

m(k*a)=(m*k)a;

4. Дистрибутивність відносно додавання:

(k+m)a=k*a+m*a;

k(a+b)=k*a+k*b;

25. Скалярним добутком двох ненульових векторів і називається число, рівне добуткові довжин цих векторів на косинус кута між ними.

Позначається або . Отже, за означенням,

Властивості скалярного добутку.

Комунікативна властивість множення:

Асоціативна властивість відносно множення на число: .

Дистрибутивна властивість відносно додавання векторів:

26. Скалярний добуток векторів дорівнює сумі добутків їхніх однойменних координат.

27.Векторним добутком вектора на вектор називається вектор , що:

1. перпендикулярний векторам і , тобто

2. має довжину, чисельно рівну площі паралелограма, побудованого на векторах і як на сторонах,тобто:

;

Векторний добуток позначається

Властивості векторного добутку.

1. Антикомунікативність множення:

2. Асоціативність відносно скалярного множника:

3. Дистрибутивність відносно додавання векторів:

4. Два ненульових вектори і колінеарні тоді і тільки тоді, коли їхній векторний добуток дорівнює нульовому векторові, тобто ║

5. _{Модуль векторного добутку не колінеарних векторів дорівнює площі паралелограма, побудованого на цих векторах, віднесений до спільного початку}

Векторний добуток через координати:

28. Розглянемо добуток векторів і , складений в такий спосіб: Тут перші два вектори перемножуються векторно, а їхній результат скалярно на третій вектор. Такий добуток називається мішаним добутком трьох векторів. Мішаний добуток являє собою деяке число.

Властивості мішаного добутку:

1.Мішаний добуток змінює свій знак при зміні місць будь-яких двох векторів-співмножників, тобто , ,

2.Мішаний добуток не змінюється при циклічній перестановці його співмножників, тобто

3.Мішаний добуток не міняється при зміні місцями знаків векторного і скалярного множення, тобто

_{4.Модуль мішаного добутку = V паралелограма, побудованого на векторах a, b, c, віднесених до спільного початку.}

Мішаний добуток ненульових векторів і дорівнює нулеві тоді і тільки тоді, коли вони компланарні:

Якщо то - компланарні.

29.Нехай у просторі площина задана точкою і вектором , перпендикулярним цій площині. Виведемо рівняння площини . Візьмемо на ній довільну точку і складемо вектор . При довільному місці точки на площині вектори и взаємно перпендикулярні, тому їх скалярний добуток дорівнює нулю: , тобто:

.

Це рівняння називається рівнянням площини, що проходить через дану точку перпендикулярно вектору .

Окремі випадки загального рівняння площини:

1. Якщо , то воно приймає, вигляд . Цьому рівнянню задовольняє точка .Отже, в цьому випадку площина проходить через початок координат.

2. Якщо , то маємо рівняння . Нормальний вектор перпендикулярний осі Oz. Отже, площина паралель осі Oz; якщо — паралель осі , — паралель осі .

3. Якщо , то площина проходить через паралель осі , тобто площина проходить через вісь . Аналогічно рівнянням і , відповідають площини, що проходять відповідно через осі і .

4. Якщо , то рівняння (12.4) приймає вигляд тобто . Площина паралельна площині. Аналогічно, рівнянням

5. і відповідають площини, відповідно паралельні площинам і .

6. Якщо , то рівняння (12.4) прикмет вигляд , тобто . Це рівняння площини . Аналогічно: — зрівняний площині ; — рівняння площини .

30. Рівняння площини, що проходить через три дані точки

Використовуємо умову компланарності трьох векторів (їх змішаний добуток дорівнює нулю), одержуємо , тобто

Рівняння площини у відрізках

Нехай площина відсікає на осях і відповідно відрізки і с тобто проходить через три точки і (див. рис. 70).

П ідставляючи координати цих точок в рівняння, отримуємо

Розкривши детермінант, маємо, тобто . або

(12.7)

Рівняння (12.7) називається рівнянням площини у відрізках на осях. Їм зручно користуватися при побудові площини.

31. Кут між площинами:

або

Якщо і площини перпендикулярні (див. рис. 73, а), то такі ж їх нормалі, тобто (і навпаки). Але тоді, тобто Отримана рівність є умова перпендикулярності двох площин і .

Якщо площина і паралельні (див. рис. 73, б), то паралельні і їх нормалі і (і навпаки). Але тоді, як відомо, координати векторів пропорційні: . Це і є умова паралельності площин і .

32. Пряму в просторі можна задати як лінію перетину двох непаралельних площин. Розглянемо систему рівнянь

Кожне з рівнянь цієї системи визначає площину. Якщо, площини не паралельні (координати векторів і не пропорційні), то система визначає пряму як геометричне місце точок простору, координати яких задовольняють кожному з рівнянь системи. Рівняння називають загальними рівняннями прямої.

33. Нехай — направляючий вектор прямої і — точка, що лежить на цій прямій. Вектор , що сполучає точку з довільною точкою прямої , паралель вектору . Тому координати вектора і вектора пропорційні:

Рівняння називаються канонічним рівняннями прямої в просторі.

34.Нехай прямі і задані рівняннями

і

Під кутом між цими прямими розуміють кут між направляючими векторами і . Тому, по відомій формулі для косинуса кута між векторами, одержуємо або

Якщо прямі і перпендикулярні, то в цьому і тільки в цьому випадку маємо . Отже, чисельник дробу (12.16) рівний нулю, тобто .

Якщо прямі і паралеьні, то паралеьні їх направляючі вектори і . Отже, координати цих векторів пропорційні, тобто .

35. Якщо задано рівняння прямої l то нескладно знайти s = {m; n; p} - напрямний вектор прямої і M1(x1, y1, z1) - координати точки що належить цій прямій. Із властивостей векторного добутку відомо, що модуль векторного добутку векторів дорівнює площі паралелограма побудованого на цих векторах

S = |M0M1×s|.

З іншого боку площа паралелограма дорівнює добутку його сторони на висоту проведену до цієї сторони

S = |s|d.

В нашому випадку висота буде дорівнювати відстані від точки до площини d, а сторона паралелограма дорівнює модулю напрямного вектора s.

Прирівняв площі нескладно отримати формулу відстані від точки до прямої:

d = |M0M1×s|/|s|

36.Нехай площина задана рівнянням , а пряма рівняннями

і пряма не перпендикулярна площині. Кутом між прямою і площиною називають гострий кут між прямою и її проекцією на площину:

Якщо пряма паралельна площин і, то вектори і перпендикулярні, а тому , тобто є умовою паралельності прямої і площини.

Якщо пряма перпендикулярна площині , то вектори і паралельні. Тому рівність

є умовами перпендикулярності прямої і площини.

Перетин прямої з площиною. Умова приналежності прямої площини

Нехай вимагається знайти точку перетину прямої

(12.18)

з площиною (12.19)

Для цього треба вирішити систему рівнянь (12.18) і (12.19). Простіше всього це зробити, записавши рівняння прямої (12.18) в параметричному вигляді:

Підставляючи ці вирази для і в рівняння площини (12.19), одержуємо рівняння або (12.20)

Якщо пряма не паралель площині, тобто якщо то з рівності (12.20) знаходимо значення :

Підставляючи знайдене значення t в параметричні рівняння прямої, знайдемо координати точки перетину прямої з площиною. Розглянемо тепер випадок, коли :

а) якщо то пряма паралель площині і перетинати її не буде (рівняння (12.20) рішення не має, оскільки має вигляд , де );

б) якщо то рівняння (12.20) має вигляд йому задовольняє будь-яке значення , будь-яка точка прямої є точкою перетину прямої і площини. Висновок: пряма лежить в площині. Таким чином, одночасне виконання рівності

є умовою приналежності прямої площини.

37.Поняття множини є одним з фундаментальних у математиці. Воно належить до понять яким не можна дати строге означення, тобто до так званих первісних, які не можна визначити через простіші поняття. Інтуєтивно множину розуміють як сукупність (сімейство, набір, зібрання, клас) деяких, обєктів об’єднаних за певною ознакою чи властивістю. Наприклад; множина студентів першого курсу, сукупність тих із них, які здали вступні екзамени без трійок і сімейство зірок Великої Ведмедиці, система трьох рівнянь з 3-ма невідомими, множина цілих чисел.  Об’єкти, із яких складається множина, називаються її елементами. Множини позначається великими буквами, а її елементи малими. Те, що елемент а належить множені А записується так а   А. Запис а  є А або а  А означає, що елемент а  не належить множені А.  Окремі найважливіші множини мають загальноприйняте позначення  · N – множина натуральних чесел (1, 2, 3, 4…)  · Z – множина цілих чисел (…-3, -2, -1, 0, 1, 2, 3…)  · Q – множина раціональних чисел (Z + дробові числа)  · I – множина всіх ірраціональних чисел  · R – множина дійсних чисел ( Q +  ірраціональні чисела)           Множина, що містить безліч елементів називається нескінченною. Приклад: множина усіх точок даного відрізку, що проходить через задану точку, множина усіх прямих паралельних заданій прямій.  Множина, яка містить скінчену кількість елементів називається скінченою.  Запис A={a₁, a₂, a₃… a_n} означає, що множина А скінчена і містить n елементів. Множина Х={x₁, x₂… , x_n….} – є незкінченою. Множина, яка не містить жодного елементу називаєтся порожньою і позначається символом  . 

Нехай задано дві множини А і В. Якщо кожен елемент множини А є елементом мнгожини В, то множину А називають підмножиною множини В і пишуть А  В (А міститься в В).  Наприклад N   Z. Очевидно, що кожна множина є своєю підмножиною, а порожня множина є підмножиною будьякої множини.  Якщо множини А і В містять одні і ті ж елементи, тобто А  В і В  А, то їх називають рівними і пишуть А=В.  Множину, різні підмножини якої доводиться розглядати в процесі вивчення якогось питання, називають універсальною множиною. 

Операції над множинами

Об’єданням двох множин А і В, називається множина А U В, елементи якої належать хочаб одній із цих множин.

A_i = A₁ U A₂ U A₃ U…U A_n 

Перерізом двох множин А і В називається множина А ∩ В елементи якої належать як і множині А, так і множені В.

A_i={x | x є А₁ і х є А₂, х є А₃…х є А_n} 

Властивості об’єдання і перерізу множин:  1.    Комутативний (переставний) закон         А U B = В U А;               А ∩ В = В ∩ А;  2.    Асоціативний (сполyчний) закон.  А ∩ (В ∩ С) = (А ∩ В) ∩ С  А U (В U С) = (А U B) U С  3.    Дистрибутивний (розподільний) закон.  А U (В ∩ С)=(А U B) ∩ (А U С)  А ∩ (В U С)=(А ∩ В) U (А ∩ С)  4.    А U Ш = А.  5.    А ∩ Ш = Ш. 

Різницею множин А та В називається множина А\В, яка складається зусіх тих елементів, які належать множині А і не належать В.

Властивості різниці :  ·       А \ В ≠ В \ А – не комутативна .  ·       А \ (В \ С)  ≠ (А \ В) \ С – не асоціативна  ·        А U Ш = А.  ·       А ∩ Ш = Ш.  ·       (B U C) \ A=(B \ A) U (C \ A) – дисрибутивний закон віднімання відносно об’єдання;  ·       (B ∩ C) \ A = (B \ A) ∩ (C \ A) – дистрибутивний закон віднімання відносно перерізу; 

Якщо А є В, то різницю В \ А називають доповненням множини А до множини В і записують -   = В \ А    

Отже, доповненням до підмножини А в множину В називається множина всіх елементів із множини В, які не належать А

Властивості доповнення, якщо  А  В 

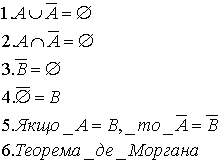
38,39,40,41.

42.Одним з основних математичних понять є поняття функції. Поняття функції пов'язано зі встановленням залежності ( зв'язки) між елементами двох множин.

Нехай дано дві не порожні множини і . Відповідність , яка кожному елементу ставить один і лише один елемент називається функцією і записується , або . Говорять ще, що функція відображає множину на множину. Змінна називається при цьому аргументом або незалежною змінною, а – функцією або залежною змінною (від ). Щодо самих величин і говорять, що вони знаходяться у функціональній залежності. Іноді функціональну залежність у від х пишуть у вигляді , не вводячи нової букви ( ) для позначення залежності. Множина називається областю визначення функції і позначається . Множина всіх називається множиною значень функції і позначається .

Найбільш часто зустрічаються три способи завдання функції : аналітичний, табличний, графічний.

Аналітичний спосіб : функція задається у вигляді однієї або декількох формул або рівнянь.

Наприклад :

Якщо область визначення функції не вказана, то передбачається, що вона співпадає з множиною всіх значень аргументу, при яких відповідна формула має сенс. Так, областю визначення функції =2 є відрізок [-1; 1].

Аналітичний спосіб завдання функції є самим зручним, оскільки до нього прикладені методи математичного аналізу, що дозволяють повністю досліджувати функцію

Графічний спосіб : задається графік функції.

Часто графіки викреслюються автоматично самописними приладами або зображаються на екрані дисплея. Значення функції , відповідні тим або іншим значенням аргументу , безпосередньо знаходяться з цього графіка.

Перевага графічного способу є його наочність, недоліком – його неточність.

Табличний спосіб : функція задається таблицею ряду значень аргументу і відповідних значень функції. Наприклад, відомі таблиці значень тригонометричних функцій, логарифмічні таблиці.

На практиці часто доводиться користуватися таблицями значень функцій, отриманих досвідченим шляхом або в результаті спостережень.