45

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЗАПОРІЗЬКИЙ КОЛЕДЖ РАДІОЕЛЕКТРОНІКИ

ЗАПОРІЗЬКОГО НАЦІОНАЛЬНОГО ТЕХНІЧНОГО УНІВЕРСИТЕТУ

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

ДО САМОСТІЙНОЇ РОБОТИ

з дисципліни: «МІКРОСХЕМОТЕХНІКА»

ЗА ТЕМАТИКОЮ: АРИФМЕТИЧНІ ТА ЛОГІЧНІ ОСНОВИ ОБЧИСЛЮВАЛЬНОЇ ТЕХНІКИ

для студентів спеціальності: 5.05080201 «Конструювання, виробництво та технічне обслуговування виробів електронної техніки»

2010

М етодичні рекомендації до самостійні роботи з дисципліни «Мікросхемотехніка» за тематикою: арифметичні та логічні основа обчислювальної техніки для студентів спеціальності: 5.05080201 «Конструювання, виробництво та технічне обслуговування виробів електронної техніки»

Укладач: Коваль О.В. – викладач вищої категорії.

Відповідальний за випуск: Довгаль О.М.

Рецензент: Рибін В.О. – заступник декана ФІОТ,

старший викладач кафедри КСМ.

Розглянуто та схвалено на засіданні циклової комісії за напрямом «Електроніка» протокол № ___ від _____________ Голова комісії ____________ І.В. Винокурова

Затверджено на засіданні методичної ради коледжу протокол № ___ від «___» ____________ 20 __ Голова методичної ради ____________ О.К. Баршай

Рецензія

В наданих на рецензію м етодичних рекомендаціях з дисципліни «Мікросхемотехніка» для студентів спеціальності 5.090805 «Конструювання, виробництво і технічне обслуговування виробів електронної техніки» розглянуті питання щодо самостійного вивчення окремих розділів предмету за тематикою: арифметичні та логічні основа обчислювальної техніки у відповідності до навчальної програми.

Окрема увага приділяється самоперевірці засвоєння теоретичного матеріалу студентами та самостійному визначенню рівня підготовки за даним розділом у відповідності до розроблених критеріїв

Рекомендації виконані на державній мові, на доступному для студентів рівні. Вони надають можливість студентам узагальнити та доповнити знання теоретичного курсу дисципліни, ґрунтуючись на здобутому під час засвоєння як лекційного так практичного матеріалу.

Надані методичні рекомендації сприяють забезпеченню системного підходу щодо вивчення даної дисципліни та послідовності викладання матеріалу, враховуючи обґрунтування зв’язку теоретичних знань з практичними навичками.

Методичні вказівки виконані на достатньо високому рівні та рекомендуються для впровадження в навчальному закладі.

Рецензент:

З МІСТ

ВСТУП. АРИФМЕТИЧНІ ТА ЛОГІЧНІ ОСНОВИ ОБЧИСЛЮВАЛЬНОЇ ТЕХНІКИ 5

1 Системи числення 7

2 Спеціальні системи числення. Критерій вибору системи числення для використання ЕОМ 10

3 Подання чисел до ЕОМ з фіксованою, плаваючою крапкою 14

4 Поняття машинного числа, переповнення розрядної сітки 20

5 Форми, діапазон і точність представлення чисел 23

6 Кодування від'ємних чисел 28

Р ІІ 7 Практичні схеми на логічних елементах сімейства ТТЛ 33

8 ТЕСТОВІ ЗАВДАННЯ ДЛЯ САМОПЕРЕВІРКИ ЗНАНЬ

СТУДЕНТІВ 39

8.1 Тестові завдання щодо засвоєння матеріалу з розділу арифметичні та логічні основи обчислювальної техніки достатнього рівня складності 39

8.2 Тестові завдання щодо засвоєння матеріалу з розділу арифметичні та логічні основи обчислювальної техніки середнього рівня складності 40

8.3 Тестові завдання щодо засвоєння матеріалу з розділу арифметичні та логічні основи обчислювальної техніки високого рівня складності 42

8.4 Критерії оцінювання 44

РЕКОМЕНДОВАНА ЛИТЕРАТУРА 45

Вступ. Арифметичні та логічні основи обчислювальної техніки

В нинішній час великий розвиток отримали цифрові методи обробки інформації, та цифрові системи на основі сучасної елементної бази.

Упорядкована взаємодіюча сукупність приладів, яка призначена для приймання, обробки, перетворення та зберігання інформації називається цифровою системою. Цифрові системи складаються з цифрових пристроїв, що є функціонально завершеними.

Спосіб подання будь-якого числа за допомогою деякого алфавіту символів(цифр) називають системою числення.

В непозиційних системах числення. Прикладом системи, в якій значення конкретної цифри постійне і не залежить від її розташування в запису числа, є Римська система запису чисел.

Позиційною називають систему числення, якщо та сама цифра має різне значення, обумовлене позицією цифри в послідовності цифр, що зображує число/

Система числення, що використовується в повсякденному житті, має десять різних цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) і тому її називають десятковою системою числення.

У комп'ютерах застосовуються такі позиційні системи числення: десяткова, двійкова, вісімкова і шістнадцяткова.

Як відомо з історії обчислювальної техніки, основу роботи цифрових схем і пристроїв становить спеціальний математичний апарат - булева алгебра, алгебра логіки або числення висловлювань. При цьому під висловлюванням розуміють будь-яке твердження, яке можна вважати істинним чи хибним.

Якщо висловлювання істинне, то вважають, що його значення дорівнює одиниці, якщо ж висловлювання хибне, то його значення дорівнює нулю. Отже, значення висловлювань можна розглядати як змінну величину, що набуває тільки двох дискретних значень: 0 чи 1. Це приводить до повної відповідності між логічними висловленнями в математичній логіці та двійковими цифрами у двійковій системі числення, що дозволяє описувати роботу логічних схем, виконувати їх аналіз і синтез за допомогою математичного апарату алгебри логіки.

Будь-який пристрій комп'ютера, що виконує арифметичні чи логічні операції, можна розглядати як функціональний перетворювач.

В алгебрі логіки існує три основних логічних функції

Конюнція АБО «І» Логічне множення			диз’юнкція АБО «ИЛИ» логічне додавання			Інверсія АБО «НІ» Логічне заперечення
X1	X2	F	X1	X2	F	X	f
0	0	0	0	0	0	0	1
0	1	0	0	1	1	1	0
1	0	0	1	0	1
1	1	1	1	1	1
F=X1.X2; X1  X2; X1&X2			F=X1+X2=X1X2			F= = X
Коньюнтор			Дезьюнктор			Інвертор

Відповідно до логічних функцій в Булевій алгебрі існують логічні елементи в цифровій схемотехніці

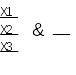
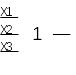
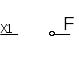
Логічний елемент «І» Логічний елемент «АБО» Логічний елемент «НІ»

Рисунок 1 – Умовне графічне позначення основних логічних елементів

На підставі перелічених логічних елементів можна реалізувати будь-яку функціонально завершену цифрову схему.