7. Смо с отказами Одноканальная смо с отказами

СМО состоит из одного канала на который поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ. Найти предельные вероятности системы и показатели ее эффективности.

Р ассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний: S₀ – свободен, S₁ – занят. Размеченный граф состояний представлен на рисунке 2.

Рисунок 2

Обозначим вероятности состояний p₀ и p ₁. p₀ - среднее время пребывания СМО в состоянии S_{0 ,} p₁ - среднее время пребывания СМО в состоянии S_1. Очевидно, что p ₀+p ₁=1.

Среднее время обслуживания равно .

Система уравнений Колмогорова для вероятностей состояний имеет вид:

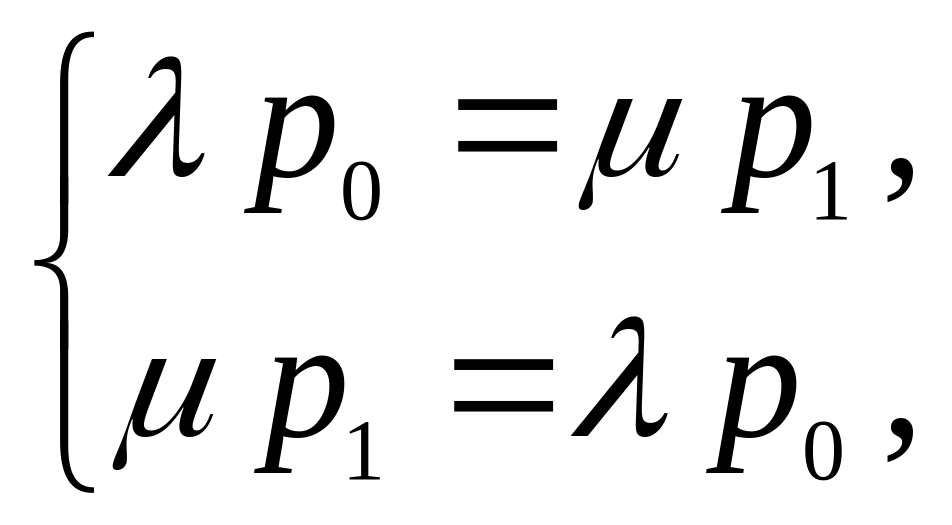
Учитывая условие , можно найти предельные вероятности состояний:

.

Предельные вероятности выражают среднее относительное время пребывания системы в состоянии (когда канал свободен) и (когда канал занят), т.е. определяют соответственно относительную пропускную способность системы и вероятность отказа :

.

Тогда абсолютную пропускную способность ( среднее число заявок, поступающих в СМО в единицу времени) можно найти так:

.

8. Многоканальная система с отказами (задача Эрланга)

Рассмотрим классическую задачу ТМО – задачу Эрланга. Имеется каналов, на которые поступает поток заявок с интенсивностью . Поток обслуживаний (выходной поток) каждого канала имеет интенсивность . Найти предельные вероятности состояний системы и показатели ее эффективности.

Система имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): , ,…, , где – состояние системы, когда в ней находится заявок, т.е. занято каналов.

Р азмеченный граф состояний соответствует процессу гибели и размножения (рис. 3).

Рисунок 3

Поток заявок переводит систему из левого состояния в соседнее правое с одной и той же интенсивностью . Интенсивность потока обслуживаний, переводящих систему из правого состояния в соседнее левое, меняется. Например, если СМО находится в состоянии (два канала заняты), то она может перейти в состояние (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживаний будет . Аналогично суммарный поток обслуживаний, переводящий СМО из состояния (три канала заняты) в , будет иметь интенсивность , т.е. может освободиться любой из трех каналов, и т.д.

По формуле для схемы гибели и размножения получим:

,

где , ,…, .

Обозначим . Величина называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала. Она выражает среднее число заявок, приходящих за среднее время обслуживания одной заявки. Тогда формулы Эрланга

.

Где

, , … , .

Вероятность отказа СМО есть предельная вероятность того, что все каналов системы будут заняты, т.е.

.

Относительная пропускная способность – вероятность того, что заявка будет обслужена:

.

Тогда абсолютная пропускная способность:

.

Среднее число занятых каналов - это математическое ожидание:

.

С другой стороны , т.к абсолютная пропускная способность - это интенсивность потока обслуженных системой заявок (в единицу времени), поскольку каждый занятый канал обслуживает в среднем заявок (в единицу времени), тогда:

.