МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

"Южно-Российский государственный университет экономики и сервиса" (ФГБОУ ВПО «ЮРГУЭС»)

Волгодонский институт сервиса (филиал)

(ВИС ФГБОУ ВПО «ЮРГУЭС»)

Ю.В. Никонорова

Основы теории массового обслуживания

Методические указания

для самостоятельной работы

для студентов очной и заочной форм обучения

направления 100100 «Сервис» бакалавриат

Волгодонск 2011

Составитель:

канд.физ.-мат.наук, доцент кафедры «Экономика и управление»

ФГБОУ ВПО ВИС ЮРГУЭС

Ю.В.Никонорова

Рецензент:

канд.физ.-мат.наук, доцент кафедры «Естественно-научные и гуманитарные дисциплины»

ФГБОУ ВПО ВИС ЮРГУЭС

А.Г. Кремлев

Методические указания разработаны для студентов - бакалавров направления 100100 «Сервис» ВИС в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования. В методических указаниях изложены основы теории массового обслуживания, вопросы к зачету по дисциплине.

© Волгодонский институт сервиса (филиал) государственного образовательного учреждения

высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса», 2011

Содержание

1. Основные понятия..................................................................................... 4

2. Классификация СМО ............................................................................... 5

3. Простейший поток.................................................................................... 6

4. Показатели эффективности...................................................................... 7

5. Уравнения Колмогорова...........................................................................7

6. Процессы гибели и рождения.................................................................. 8

7. СМО с отказами.

Одноканальная СМО с отказами................................................................. 9

8. Многоканальная система с отказами (задача Эрланга)......................... 10

10. СМО с ожиданием (с очередью)

Одноканальная СМО с ожиданием и с ограничением на длину очереди.......................................................................................................... 11

Одноканальная СМО с (неограниченным) ожиданием.................. 12

Вопросы к зачету ................................................................................. 13

Библиографический список......................................................................... 15

1. Основные понятия

Теория массового обслуживания (теория очередей) — раздел теории вероятностей, целью исследований которого является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящие из неё, длительности ожидания и длины очередей.

Первые задачи ТМО (Теории Массового Обслуживания) были рассмотрены сотрудником Копенгагенской телефонной компании, ученым Агнером Эрлангом, в период между 1908 и 1922 годами. Перед Эрлангом стояла задача упорядочить работу телефонной станции и заранее рассчитать качество обслуживания потребителей в зависимости от числа используемых устройств.

При исследовании операций часто приходится сталкиваться с работой своеобразных систем, называемых системами массового обслуживания (СМО). Примерами таких систем могут служить: торговые базы, телефонные станции, автозаправочные станции, поликлиники, ремонтные мастерские, билетные кассы, справочные бюро, порты, магазины, парикмахерские, системы сбора и обработки информации, автоматизированные производственные цеха, поточные линии, транспортные системы, системы ПВО и т. п. Каждая СМО состоит из какого-то числа обслуживающих единиц (или «приборов»), которые называются каналами обслуживания. Каналами могут быть: линии связи, рабочие точки, кассиры, продавцы, лифты, автомашины и др. СМО могут быть одноканальными и многоканальными.

Система массового обслуживания (СМО) - система, которая производит обслуживание поступающих в неё требований.

Всякая СМО предназначена для обслуживания какого-то потока заявок (или «требований»), поступающих в какие-то случайные моменты времени. Обслуживание заявки продолжается какое-то, случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времен обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок (они либо становятся в очередь, либо покидают СМО необслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

Требование (заявка) — запрос на обслуживание.

Входящий поток требований — совокупность требований, поступающих в СМО.

Время обслуживания — период времени, в течение которого обслуживается требование.

Математическая модель СМО — это совокупность математических выражений, описывающих входящий поток требований, процесс обслуживания и их взаимосвязь.

П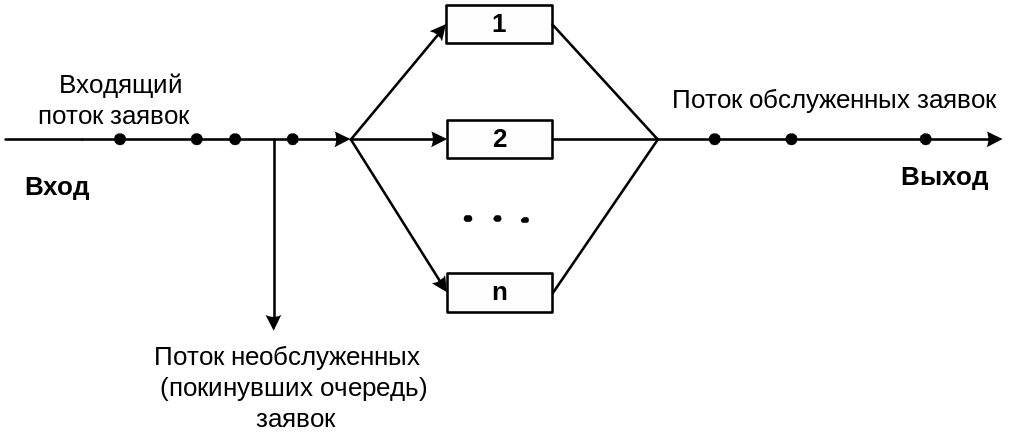 редмет теории массового обслуживания — построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с показателями эффективности СМО, описывающими ее способность справляться с потоком заявок. В качестве таких показателей (в зависимости от обстановки и целей исследования) могут применяться разные величины, например: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания; вероятность того, что число заявок в очереди превысит какое-то значение, и т. д.

Схема СМО