Частотные характеристики параллельного резонансного контура

В параллельном резонансном контуре (рис.2.37а) активная проводимость не зависит от частоты, а индуктивная, ёмкостная и реактивная проводимости изменяются в соответствии со следующими выражениями:

B_L() = 1/ωL;

B_C() = ωC;

B() = B_L()- B_C();

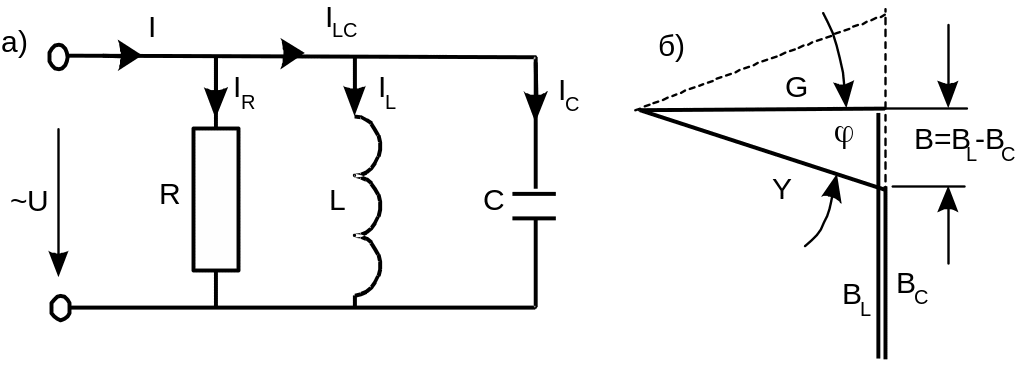
Рис. 2.37

Полная проводимость, как следует из треугольника проводимостей (рис.2.37б):

Y()=√(G²+B²).

Вид этих зависимостей от частоты представлен на рис.2.38а.

При изменении частоты и неизменном приложенном напряжении токи изменяются пропорционально соответствующим проводимостям:

I() = UY);

I_L() = U/L;

I_C = UC,

I_LC = UB().

При резонансной частоте =₀ ток I, потребляемый от источника, имеет минимум и равен току в активном сопротивлении I_R, а ток на реактивном участке цепи I_LС равен нулю (см. рис. 2.38а). Реальные кривые могут несколько отличаться от рассмотренных идеальных, так как здесь не учитывалось активное сопротивление катушки.

Рис. 2.38

Угол сдвига фаз (рис. 2.38б) изменяется в соответствии с выражением:

φ = arctg[(1/L-C)/G].

При <₀ цепь носит индуктивный характер (ток отстаёт от напряжения на угол ), при =₀ - активный, а при >₀ - ёмкостный (ток опережает напряжение). Если Q>1, то при резонансе токов I_L(_) и I_C(_) превышают ток источника I в Q раз.

На рис. 2.38б кроме () построены также зависимости от частоты полного Z() и реактивного X() сопротивлений. B общем случае (см.сплошные линии на рисунке):

Z() = 1/Y() = 1/√(G²+B²);

X() = B/(G²+B²).

При резонансе полное сопротивление принимает максимальное значение а реактивное обращается в ноль. В идеализированном случае, когда активная проводимость настолько мала, что ей можно пренебречь (G=0):

X() = 1/B;

Z() = 1/|B|.

Тогда в точке резонанса кривые X() и Z() имеют разрыв (см. пунктирные линии на рис.2.38б).

Лабораторная работа № 4 «Исследование цепей переменного тока»

Цель работы: Исследование цепей переменного тока: экспериментальная проверка законов Ома и Кирхгофа, построение векторных диаграмм и составление баланса мощности.

Задание к лабораторной работе

1. Для схемы (рис. 1) с последовательным соединением резистора и конденсатора рассчитайте и измерьте действующие значения падений напряжения на резисторе U_R и конденсаторе U_C, ток I, угол сдвига фаз , полное сопротивление цепи Z и емкостное реактивное сопротивление X_C. Результаты занесите в табл. 1. Постройте векторную диаграмму.

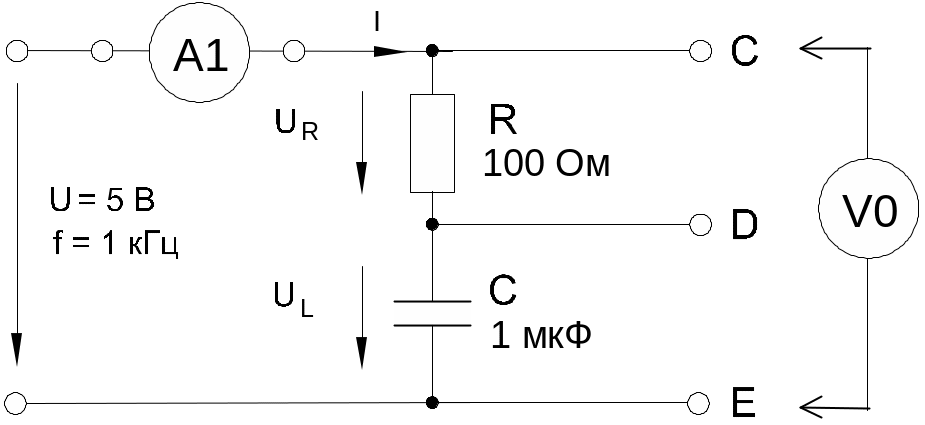
Рис. 1

2. Для схемы (рис. 2) с параллельным соединением резистора и конденсатора рассчитайте и измерьте действующие значения тока в резисторе I_R и конденсаторе I _C, полный ток I и вычислите угол сдвига фаз , полное сопротивление цепи Z и емкостную реактивную проводимость B_C. Результаты занесите в табл.2. Постройте векторную диаграмму.

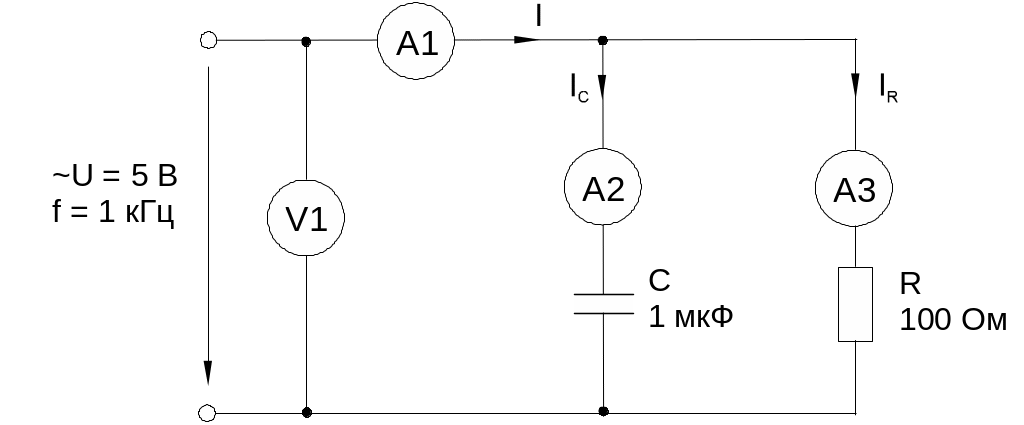
Рис. 2

3. Для схемы (рис. 3) с последовательным соединением резистора и катушки индуктивности рассчитайте и измерьте действующие значения падений напряжения на резисторе U_R и катушке U_L и ток I. Вычислите угол сдвига фаз , полное сопротивление цепи Z, индуктивное реактивное сопротивление X_L и фазовый сдвиг между полным напряжением цепи U и падением напряжения на катушке U_L. Активным сопротивлением катушки ввиду его малой величины можно при этом пренебречь. Результаты занесите в табл. 3. Постройте векторную диаграмму.

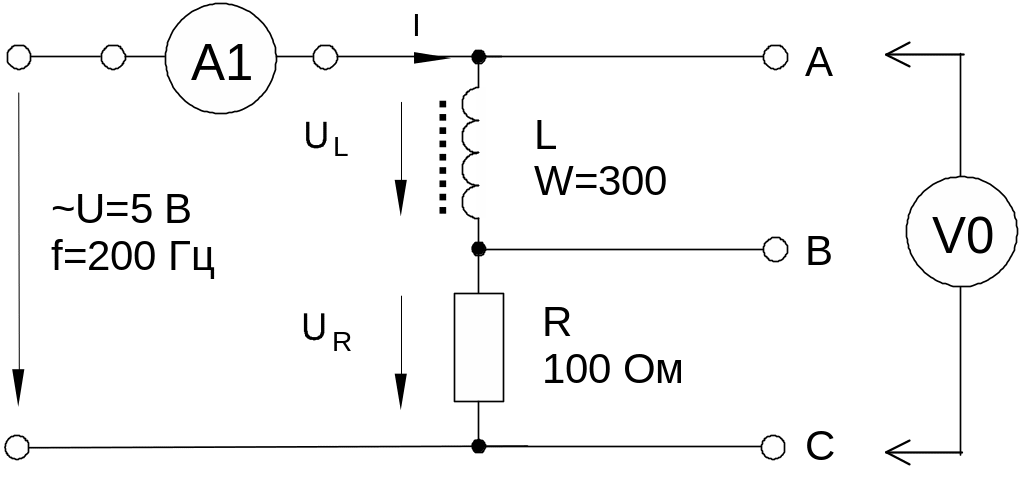
Рис. 3

4. Для схемы (рис. 4) с параллельным соединением резистора и катушки индуктивности рассчитайте и измерьте действующие значения тока в резисторе I_R и катушке I_L, полный ток I и вычислите угол сдвига фаз , полное сопротивление цепи Z и индуктивную реактивную проводимость B_L. Результаты занесите в табл.4. Постройте векторную диаграмму.

Рис. 4

5. Для схемы (рис. 5) рассчитайте и измерьте с помощью виртуальных приборов токи и мощности в цепи синусоидального тока. Проверьте баланс активных и реактивных мощностей. Результаты занесите в табл. 5. Постройте векторную диаграмму.

Рис.5.

Порядок выполнения лабораторной работы

1. Соберите цепь согласно схеме (рис. 1), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.

Выполните мультиметрами или виртуальными приборами измерения действующих значений тока и падений напряжений, указанных в табл.1. При измерениях падений напряжений подключайте мультиметр или канал V0 коннектора к зажимам C-E, C-D, D-E:

Таблица 1.

U, B	UR, B	UC, B	I, мА	, град	R, Ом	XC, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

Вычислите:

Угол сдвига фаз

 = arctg (U_C  U_R).

Полное сопротивление цепи

Z = U  I.

Активное сопротивление цепи

R = Z cos .

Емкостное реактивное сопротивление цепи

X_C = Z sin .

Если вы работаете с виртуальными приборами, то измерьте с помощью блока «Приборы II» R, , X_C, Z и запишите их значения также в табл. 1 под рассчитанными величинами. Сравните результаты.

Выберите масштабы и постройте векторную диаграмму напряжений (рис. 6) и треугольник сопротивлений (рис. 7).

Рис. 6 Рис. 7

2. Соберите цепь согласно схеме (рис. 2), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.

Выполните измерения U, I, I_C, I_R и занесите результаты в табл. 2. Если измерения производите виртуальными приборами, то измерьте также R, , X_C, Z.

Таблица 2

U, B	I, мА	IС, мА	IR, мА	, град	R, Ом	XC, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

Вычислите и запишите в таблицу:

Фазовый угол

 = arctg (I _C  I _R).

Активные проводимость цепи и сопротивление цепи

G = I_R  U ; R = U  I_R.

Емкостные реактивные проводимость и сопротивление цепи

B_C = I_C  U ; X_C = U  I_C.

Полные проводимость и сопротивление цепи

; Z = 1  Y.

Сравните результаты вычислений с результатами виртуальных измерений (если они есть).

Постройте векторную диаграмму токов (рис. 8) и треугольник проводимостей (рис. 9).

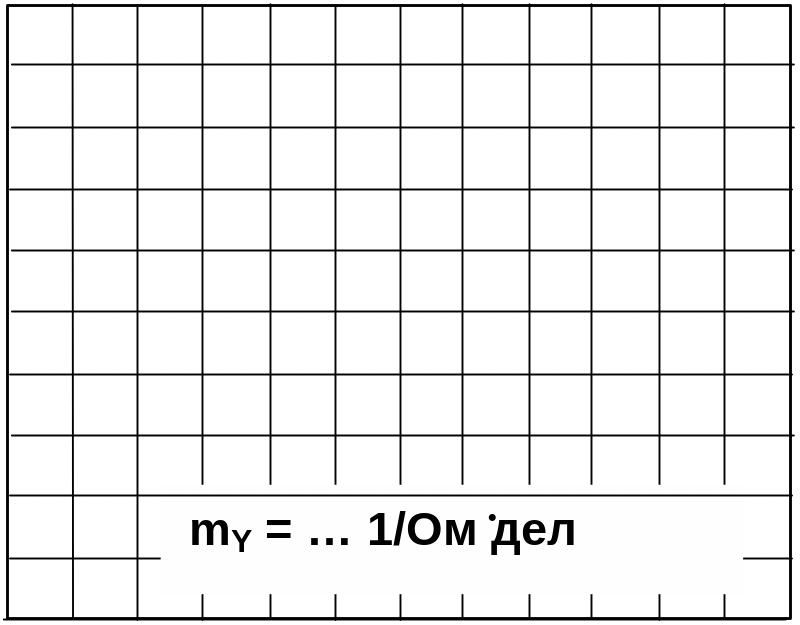
Рис. 8 Рис. 9

3. Соберите цепь согласно схеме (рис. 3), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).

Выполните измерения тока и падений напряжений, указанных в табл. 3. Если измерения производятся виртуальными приборами, то измерьте также R, , X_L, Z.

Таблица 3.

U, B	UL, B	UC, B	I, мА	, град	R, Ом	XL, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

Вычислите

Угол сдвига фаз

 = arctg (U_L  R).

Полное сопротивление цепи

Z = U  I.

Индуктивное реактивное сопротивление цепи

X_L = U_L  I

Занесите результаты вычислений в табл. 3 и сравните с результатами виртуальных измерений, если они есть. Выберите масштабы и постройте векторную диаграмму напряжений (рис. 10) и треугольник сопротивлений (рис. 11).

Рис. 10 Рис. 11

4. Соберите цепь согласно схеме (рис.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).

Выполните измерения U, I, I_L, I_R и занесите результаты в табл. 4. Если измерения производятся виртуальными приборами, то измерьте также R, , X_L, Z и вычислите G = 1/R, B_L = 1/X_L и Y = 1/Z. Занесите эти результаты в строку «виртуальные измерения» табл. 4.

Таблица 4

U, B	I, мА	IL, мА	IR, мА	, град	G, 1/Ом	BL, 1/Ом	Y, 1/Ом	Примечание
								Расчет
								Вирт. изм

Вычислите

Фазовый угол

 = arctg (I _L  I _R ).

Активная проводимость цепи

G = I_R  U.

Индуктивная реактивная проводимость

B_L = I_L  U.

Полная проводимость

Y = I  U.

Занесите результаты вычислений в таблицу и сравните с результатами измерений виртуальными приборами, если они есть. Выберите масштаб и постройте векторную диаграмму токов (рис. 12) и треугольник проводимостей (рис. 13).

Рис. 12 Рис. 13

5. Перед проведением исследований разветвленной схемы (рис. 5):

- измерьте омметром активное сопротивление R_к катушки индуктивности 40мГн:

- вычислите реактивные сопротивления катушки X_L (L=40 мГн) и конденсатора X_C (С=1 мкФ):

Соберите цепь согласно схеме (рис. 5), включив в неё виртуальные приборы V1 и A1 и виртуальные или реальные приборы А2 и А3.

Подайте синусоидальное напряжение частотой 500 Гц и установите максимальную амплитуду напряжения генератора.

Активизируйте виртуальные приборы: для измерения напряжения и тока на входе цепи, а также активной и реактивной мощности источника.

Примечание:

Избегайте включать одновременно большое количество виртуальных приборов в основном блоке. Это уменьшает количество отсчётов и снижает точность измерений!

Запишите в табл. 5 значения токов I_RL, I_R, I_C и мощностей Р_ист и Q_ист.

Таблица. 5

Ветвь	RкL	R	C	Баланс мощностей, мВт, мВАр
I, мА
Р=I2R,мВт			0	Рист		Pпотр
Q=I2X, мВАр		0		Qист		Qпотр

Вычислите по приведённым в табл. 5 формулам значения активной и реактивной мощностей каждого потребителя. Вычислите сумму активных и алгебраическую сумму реактивных мощностей их суммы и проверьте баланс мощностей.

Содержание отчета:

1. Цель работы.

2. Схемы рис. 1 … рис. 5.

3. Расчетная часть работы.

4. Таблица 1 … таблица 5.

5. Векторные диаграммы, треугольники сопротивлений и проводимостей.

6. Выводы.

Контрольные вопросы к защите лабораторной работы:

1. Сформулируйте определение синусоидального тока, амплитудного значения, фазы, начальной фазы, угловой частоты.

2. Что называется действующим значением синусоидального тока? Как связаны действующее и амплитудное значения синусоидального переменного тока?

3. Сформулируйте закон Ома для цепи синусоидального тока.

4. Треугольник сопротивлений. Дайте понятие активного, реактивного и полного сопротивлений цепи.

5. Как определяется среднее значение периодического синусоидального тока?

6. Напишите закон Ома и законы Кирхгофа в комплексной форме записи.

7. Цепь состоит из идеальной индуктивности L. Записать комплексное сопротивление цепи, построить векторную диаграмму и показать, что угол .

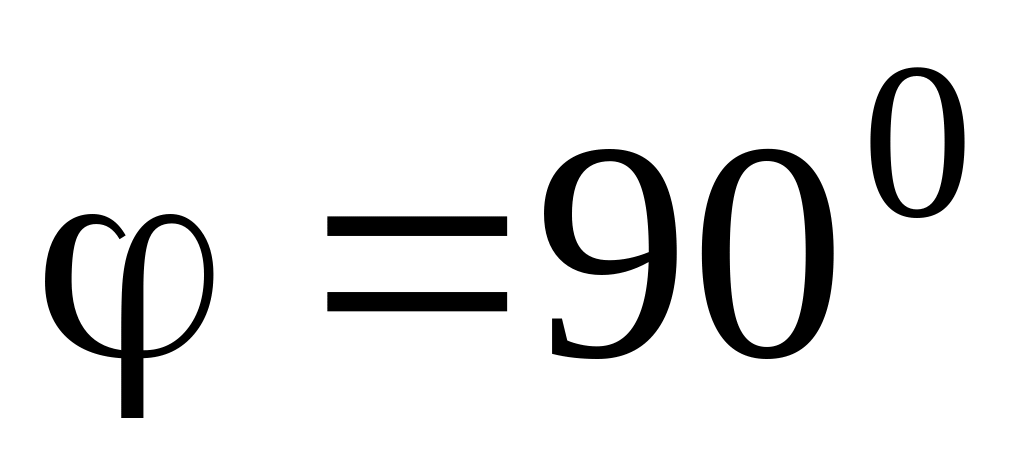8. Цепь состоит из идеального конденсатора C. Записать комплексное сопротивление z_C , построить векторную диаграмму и показать, что угол .

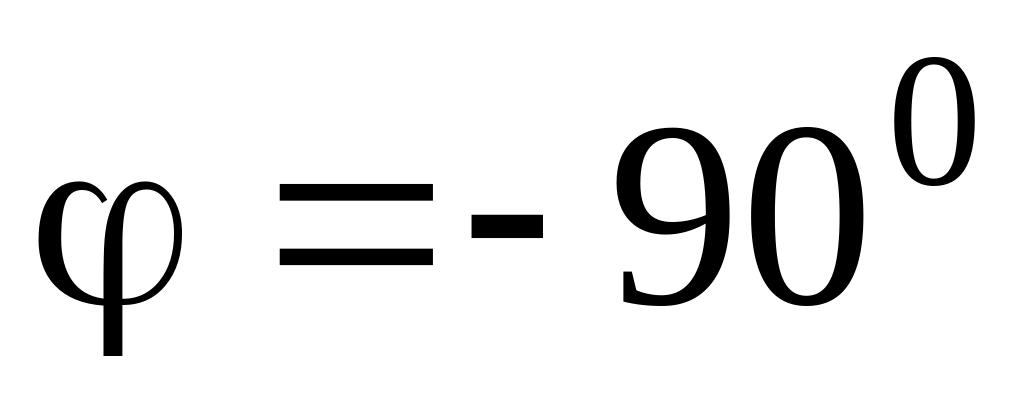9. Поясните порядок построения векторной диаграммы.