§2.13 Электромагнитные волны в вакууме.
Электромагнитное поле, как известно полностью описывает уравнение Максвелла которые в вакууме будут иметь вид
Уравнение для
совпадает с волновым уравнением решение
которого было найдено в § 2.1. Точно также:
То есть мы получим волновое уравнение. Таким образом решение уравнения Максвелла в вакууме будет иметь вид волновых функций. Для простоты рассмотрим сначала случай гармонических волн.
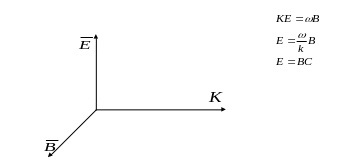
То есть мы ищем решение уравнения Максвелла в виде плоских монохроматических волн.
Подставим решение в уравнение Максвелла
при этом учтём, что оператор
можно
заменить на
§ 2.14 Энергия электромагнитного поля. Вектор Умова-Пойтинга
Рассеем некоторый замкнутый объём V ограниченно замкнутой поверхности S в котором существует электромагнитное поле.
Предположим, что это поле обладает
энергией плотность которой u.
Тогда полная энергия электромагнитного
поля будет
Вычислим
.
Изменение энергии в объёме V
может происходить по двум причинам: за
счёт переноса энергии через поверхность
S и за счёт мощности всех
сил действующих в системе. Смотри §2.4.
Для вычисления переносим через поверхность
S, введём вектор
,
где
скорость переноса энергии, которая
называется плотностью потока энергии.
Тогда энергия переноса в единицу времени,
через ds, будет
(смотри Электроток. Уравнение
непрерывности). Так как это будет энергия,
выносим из объёма
направленная наружу, то за единицу
времени энергия в объёме уменьшится на
величину -
.
Если внутри объема V имеются электромагнитные заряды, то электронное поле будет совершать работу, что приведёт к уменьшению энергии поля (работа магнитного поля равна 0)
В § « Законы электрического тока» было
показано, что мощность электромагнитных
сил в единицу объёма вещества будет
поэтому за единицу времени энергия
электромагнитного поля в объёме V
уменьшится на величину -
Так как это равенство должно выполняться для любого объекта V
Рассмотрим уравнение Максвелла в сфере.
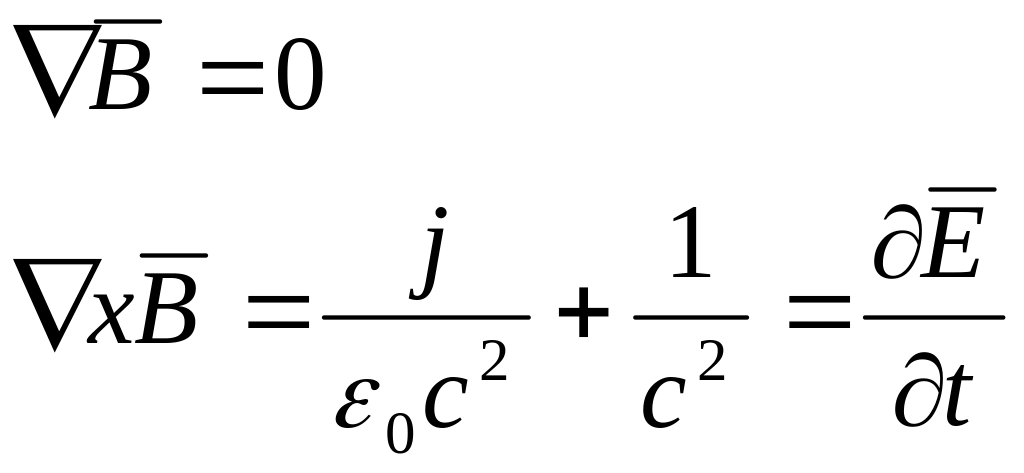
Рассмотрим
Сравнивая полученное выражения, находим, что плотность энергии электромагнитного поля будет
Вектор Умова-Пойтинга
Для того чтобы убедится, что полученные
результаты верны вспомни §2.13, что
,
тогда
Таким образом электромагнитное поле
обладает энергией, плотность которой
Часть 4 Квантовая механика.
§1 Экспериментальные основы квантовой механики.
К началу 20го века основные физические явления были объяснены классической физикой за исключение нескольких явлений:
1) тепловое излучение тела. Как известно
любая движущаяся с ускорением заряженная
частица излучает электромагнитные
волны. Так как все тела содержат заряженные
частицы, то при температуре выше
абсолютного 0 они двигаются. Поэтому
любое тело при T>0 излучает
электромагнитные волны частота которых
от 0 до
Пусть энергия излучает электромагнитные
волны за единицу времени приходящаяся
на единицу поверхности в интервале
частот от
до
будет
спектральная
плотность излучения.
С помощью
классической электродинамики Максвелла
можно получить зависимость
-закон
Релея и Джинкса или «ультрафиолетовой
катастрофой»
2) Фотоэффект, который состоял в том, что электромагнитная волна вырывала с поверхности проводника электромагнит. Само это явление легко объясняется классической электродинамикой. Под действие электромагнитного поля электроны проводника начинают двигаться вдоль поверхности.
A на движение электронов
со стороны
со стороны магнитного поля направленного
наружу и она приводит к выражению.
Столетов экспериментом установил, что увеличение амплитуды волны то есть энергии волны, скорость вылетевших электронов не меняется, а меняется их число, что невозможно объяснить классической физикой.
3) Опыты по дифракции электрона
1. Опыт с пулями
Будем описывать попадание пуль в мишень вероятность попадания P. Если открыть оба отверстия то вероятности попадания складываются.
2. Опыт с волнами
Если открыть одно отверстие то (§2.6) будем наблюдать дифракцию, если второе-дифракцию
Если оба то интерференцию
3. Опыт с электронами
p- вероятность попадания в мишень.
Вероятности не складываются, а интерферируются
Электроны описывают вероятности как пули, а вероятности интерферируются как у волн.