Лабораторна робота № 1

Тема роботи: Логічні елементи і схеми

Мета роботи : Ознайомлення з основними характеристиками логічних елементів і основами синтезу логічних схем.

Теоретичні відомості

Дана робота присвячена вивченню найпростіших комбінаційних логічних пристроїв, що реалізують логічні функції додавання, множення і заперечення.

Аналіз комбінаційних пристроїв зручно проводити за допомогою алгебри логіки, що оперує тільки з двома поняттями: істинним (логічна 1) і хибним (логічний 0). В результаті, функції, що відображають інформацію, приймають в кожен момент часу тільки значення 0 або 1. Такі функції називають логічними, а сигнали (вхідні і вихідні змінні) - двійковими (бінарними).

Схемні елементи, за допомогою яких здійснюється перетворення двійкових сигналів, які поступають на їх входи, і безпосереднє виконання передбачених логічних операцій, називають логічними пристроями.

У загальному випадку логічний пристрій може мати n входів і m виходів. Розглядаючи вхідні сигнали х₁, х₂, ..., х_n в якості аргументів, можна відповідні вихідні сигнали представляти у вигляді функції у_i = F (х₀, х₁, х₂, ..., х_n) за допомогою операцій алгебри логіки.

У булевої алгебри виділяють три основні функції: кон'юнкція, диз'юнкція, заперечення. Решта функцій є похідними від наведених вище.

• логічне додавання або диз'юнкція, позначуване символом "v" (або "+") і зване також операцією АБО. При цьому число аргументів (доданків х) може бути будь-яким. Ця операція для функції двох змінних x1 і x2 описується у вигляді логічної формули

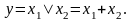
Це означає, що у істинно (дорівнює 1), якщо істинно хоча б одне з доданків x1 чи x2. І тільки у випадку, коли всі доданки х дорівнюють 0, результат логічного додавання у також дорівнює 0.

• логічне множення або кон'юнкція, позначуване символом " Ʌ " (або "∙") і зване також операцією І. При цьому число аргументів (співмножників х) може бути будь-яким. Ця операція для функції двох змінних x1 і x2 описується у вигляді логічної формули

Це означає, що у істинно (дорівнює 1), якщо істинні співмножники x1 і x2. У разі, якщо хоча б один із співмножників дорівнює 0, результат логічного множення у дорівнює 0.

• логічне заперечення або інверсія, позначуване рискою над змінною і зване операцією НЕ. Ця операція записується у вигляд

Це означає, що у істинно (дорівнює 1), якщо х хибне (дорівнює 0), і навпаки. Очевидно, що операція у виконується над однією змінною х і її значення завжди протилежно цієї змінної.

Основні логічні операції АБО, І та НЕ дозволяють аналітично описати, а логічні елементи АБО (діз'юнктор), І (кон'юнктор) і НЕ (інвертор) - реалізувати комбінаційне пристрій будь-якого ступеня складності, тобто операції 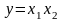володіють функціональною повнотою і становить функціонально повний набір.

_{В якості прикладу розглянемо функцію нерівнозначності у двох змінних}

х₁ і х₂, що приймають значення 1 при х₁ х₂ і значення 0 при х₁ = х₂ = 0 або при х₁ = х₂ = 1, тобто .

Операцію нерівнозначності частіше називають підсумовуванням за модулем 2 і позначають