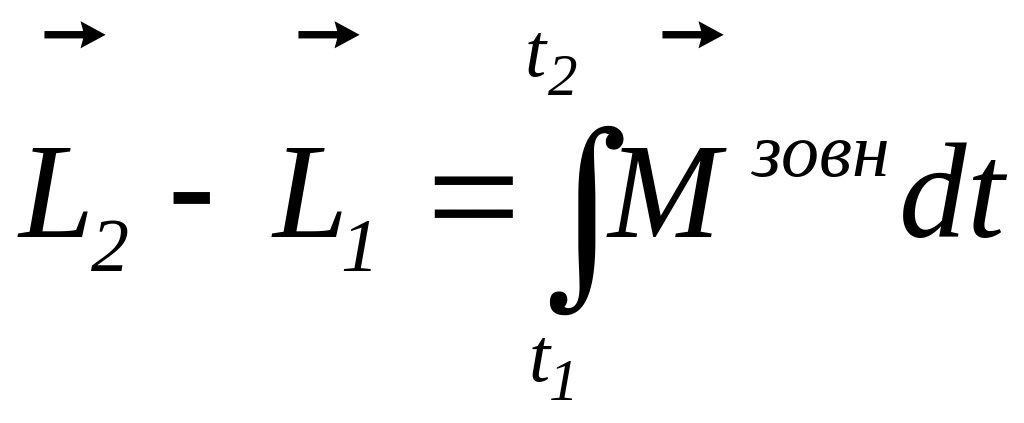9. Динаміка обертового руху.

1. Момент сили та момент імпульсу матеріальної точки відносно довільного центру.

Аналіз руху механічних систем вказує на існування ще однієї механічної величини, крім енергії та імпульсу, якій також властивий закон збереження. Це – момент імпульсу матеріальної точки (момент кількості руху).

Нехай – це радіус-вектор м.т. А відносно деякої нерухомої т. О вибраної системи відліку, а – її імпульс (т. О називають початком або полюсом).

Моментом імпульсу м.т. А відносно т. О називають вектор , що дорівнює векторному добутку векторів і :

(9.1)

З означення випливає, що є аксіальним вектором. Модуль вектора дорівнює:

,

(9.2)

де – кут між векторами і , – плече вектора відносно т. О (див. рис. 9.1).

Н а рис. 9.2 теж показані вектори для випадку, коли кут між векторами дорівнює 90^о.

Візьмемо похідну від виразу (9.1) по часу:

Так як т. О нерухома, то , значить ║ , тому . Згідно другого закону Ньютона , де  – рівнодійна всіх сил, прикладених до м.т. Отже:

(9.3)

Величину, що стоїть в правій частині (9.3), називають моментом сили відносно точки О:

(9.4)

Як і вектор аксіальний вектор. Модуль дорівнює:

,

(9.5)

де l – плече сили відносно т. О.

Отже, похідна по часу від моменту імпульсу м.т. відносно деякої нерухомої т. О дорівнює моменту сили відносно тієї ж т. О:

(9.6)

Рівняння (9.6) називають рівнянням моментів.

З означення моменту сили (9.4) випливає, що момент сили не зміниться, якщо точку прикладання сили перенести в будь-яку іншу точку, розташовану на лінії дії сили (рис. 9.3).

Якщо , то на основі властивості векторного добутку:

(9.7)

Момент рівнодійної двох або декількох сил відносно деякої точки дорівнює геометричній сумі моментів складових сил відносно тієї ж точки.

Рівняння моментів (9.6) дозволяє розв’язати дві задачі:

1. Знайти момент сили відносно т. О в момент часу t, якщо відома залежність від часу моменту імпульсу м.т. відносно тієї ж т. О.

2. Визначити приріст моменту імпульсу м.т. відносно т. О за довільний проміжок часу, якщо відома залежність від часу моменту сили , що діє на цю м.т. (відносно тієї ж т. О).

Перша задача розв’язується знаходженням похідної по часу від моменту імпульсу, тобто . Друга задача розв’язується інтегруванням рівняння (9.6). Помножимо обидві частини його на , одержимо: . Інтегруємо цей вираз:

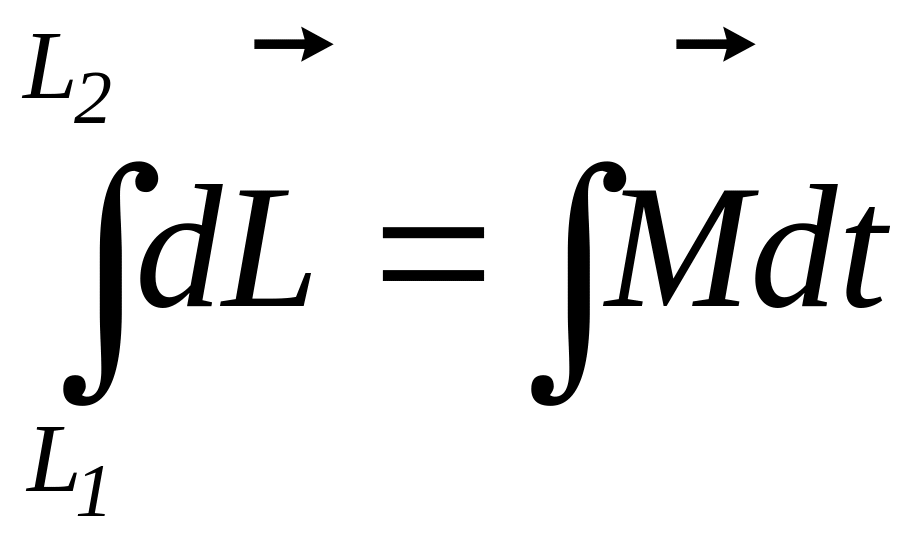
(9.8)

Величину, що стоїть в правій частині (9.8), називають імпульсом моменту сили.

Отже, приріст моменту імпульсу м.т. за довільний проміжок часу дорівнює імпульсу моменту сили за цей час.

2. Закон збереження моменту імпульсу замкненої системи.

Рівняння моментів легко узагальнити на випадок довільної системи матеріальних точок.

Моментом імпульсу системи м.т. відносно т. О називається векторна сума моментів імпульсу всіх м.т. системи відносно тієї ж т. О:

Момент всіх сил, що діють на систему м.т., визначається як векторна сума моментів окремих сил:

Сили, що діють на кожну м.т. системи, можна поділити на зовнішні і внутрішні, тому:

Записавши рівняння (9.6) для кожної м.т. даної системи і почленно додавши, одержимо:

Внутрішні сили – це сили взаємодії між м.т. даної системи. За третім законом Ньютона ці сили попарно однакові за модулем, протилежно направлені та лежать на одній прямій, тобто їх плечі однакові (див. рис. 9.4). Тому моменти сил кожної пари однакові за модулем і протилежні за напрямком; отже, вони компенсують один одного. Таким чином, сумарний момент всіх внутрішніх сил дорівнює нулю:

Отже, рівняння моментів для системи матеріальних точок має вид:

(9.9)

Похідна моменту імпульсу системи м.т. відносно довільної нерухомої т. О дорівнює геометричній сумі моментів всіх зовнішніх сил відносно тієї ж т. О.

Як і у випадку однієї м.т. з рівняння (9.9) випливає, що приріст моменту імпульсу системи за довільний проміжок часу дорівнює імпульсу сумарного моменту всіх зовнішніх сил:

(9.10)

Якщо момент зовнішніх сил відносно нерухомої т. О дорівнює нулю, то момент імпульсу системи відносно тієї ж т. О залишається сталим

Це твердження називають законом збереження моменту імпульсу. Для ізольованої системи за означенням, тому момент імпульсу ізольованої системи зберігається. Якщо зовнішні сили, що діють на матеріальні точки системи, центральні і центром сил є т. О, то момент їх відносно т. О дорівнює нулю, отже, момент імпульсу такої системи відносно т. О зберігається.

Поряд з законами збереження імпульсу та енергії закон збереження моменту імпульсу є одним з найважливіших фундаментальних законів фізики.