- •1. Сложение матриц
- •2. Умножение матриц
- •Матричные операции
- •4. Методы вычисления определителей.
- •5. Линейные неоднородные системы уравнения
- •6. Решение системы линейных уравнений матричным способом
- •7. Определители второго порядка, их свойства
- •8. Определитель третьего и п-го порядка, их свойства
- •9. Алгебраические дополнения и миноры
- •10. Понятие обратной матрицы. Ранг матрицы, его свойства
- •11. Система линейных уравнений. Однородные системы
- •12. Теория Кронекера-Капелли
- •Необходимость
- •Достаточность
- •13. Матричная запись системы линейных уравнений
- •14. Метод решения системы с помощью обратной матрицы
- •15. Решение системы линейных уравнений методом Крамера
- •16. Решение системы линейных уравнений методом Гаусса
- •17. Система линейных неравенств
- •18. Векторы. Основные понятия
- •19. Линейные операции над векторами
- •20. Скалярное произведение векторов, его свойства
- •Свойства скалярного произведения.
- •21. Векторное произведение векторов, его свойства
- •Свойства векторного произведения.
- •22. Базис. Коллинеарность и компланарность
- •23. Условие ортогональности двух векторов
- •25. Разложение вектора по ортам координатных осей
- •26. Модуль вектора. Направляющие косинусы
- •27. Действия над векторами, заданными проекциями
- •28. Смешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
22. Базис. Коллинеарность и компланарность
Коллинеа́рность — отношение параллельности векторов: два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допусти́м синоним — «параллельные» векторы.
Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).
Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости
Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.
Приведем некоторые рассуждения, основываясь на этих определениях.
Рассмотрим пространство n-мерных векторов.
Покажем, что размерность этого пространства равна n.
Возьмем
систему из n единичных векторов
вида
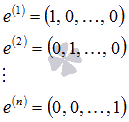 Примем
эти векторы в качестве строк матрицы А.
В этом случае матрица А будет
единичной матрицей размерности n на n.
Ранг этой матрицы равен n (при
необходимости смотрите статью ранг
матрицы: определение, методы нахождения).
Следовательно, система векторов
Примем
эти векторы в качестве строк матрицы А.
В этом случае матрица А будет
единичной матрицей размерности n на n.
Ранг этой матрицы равен n (при
необходимости смотрите статью ранг
матрицы: определение, методы нахождения).
Следовательно, система векторов ![]() линейно
независима, причем к этой системе нельзя
добавить ни одного вектора, не нарушив
ее линейной независимости. Так как число
векторов в системе
равно n,
то размерность пространства n-мерных
векторов равна n, а единичные
векторы
являются
базисом этого пространства.
линейно
независима, причем к этой системе нельзя
добавить ни одного вектора, не нарушив
ее линейной независимости. Так как число
векторов в системе
равно n,
то размерность пространства n-мерных
векторов равна n, а единичные
векторы
являются
базисом этого пространства.
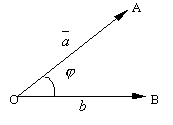
23. Условие ортогональности двух векторов
Ортогональные вектора=перпендикулярные вектора
Условие ортогональности двух векторов:
![]() или
или ![]() .
.
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
24. Проекция вектора на ось
Пусть в пространстве даны два
вектора Рассмотрим
ось l и отложим на ней единичный
вектор Под углом между
вектором
и
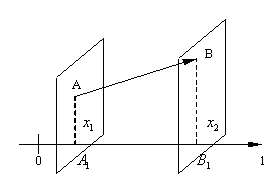
осью l понимают угол Итак, пусть l –
некоторая ось и Обозначим через A1 и B1 проекции на ось lсоответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l. Тогда проекцией вектора Проекцию
вектора
на
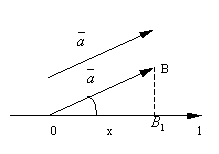
ось l будем обозначать Ясно, что если угол между вектором и осью l острый, то x2> x1, и проекция x2 – x1> 0; если этот угол тупой, то x2< x1 и проекция x2– x1<0. Наконец, если вектор перпендикулярен оси l, то x2= x1 и x2– x1= 0. Таким образом, проекция вектора на ось l – это длина отрезка A1B1, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр. Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор. Рассмотрим некоторые основные свойства проекций.
Доказательство.
Ясно, что проекция вектора не изменится
при его параллельном переносе, поэтому
достаточно рассмотреть случай, когда
начало вектора совпадает с началом
отсчёта O оси l. Так как координата
проекции начала равна нулю, то
обозначим
Доказательство.
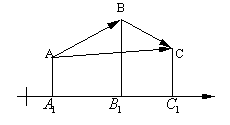
Пусть Это свойство можно обобщить на случай любого числа слагаемых.
Доказательство.
Пусть угол между вектором
и
осью Если λ > 0, то
вектор При λ > 0 Если же λ <
0, то
и
имеют
противоположные направления и
вектор
составляет
с осью угол π – φ и Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось. |
|

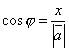 .
Откуда
.
Откуда 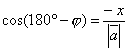 .
Т.е.
.
Т.е. 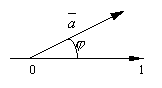 .
.