9. Алгебраические дополнения и миноры

Алгебраическим дополнением элемента   матрицы   называется число

,

Минор 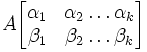  матрицы   ― определитель такой квадратной матрицы   порядка   (который называется также порядком этого минора), элементы которой стоят в матрице   на пересечении строк с номерами   и столбцов с номерами  .

Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ―угловым или ведущим главным.

Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.

Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.

10. Понятие обратной матрицы. Ранг матрицы, его свойства

Рангом матрицы A называется наибольший из порядков миноров матрицы A , отличных от нуля. Ранг нулевой матрицы считается равным нулю.

Алгоритм вычисления ранга матрицы:

• матрица приводится к ступенчатому с помощью элементарных преобразований;

• количество ненулевых строк в полученной матрице будет равно рангу первоначальной матрицы.

Свойства ранга матрицы:

• ранг матрицы не превосходит меньшего из ее размеров;

• ранг матрицы равен нулю тогда и только тогда, когда матрица нулевая;

• ранг матрицы не изменится, если из нее вычеркнуть все нулевые строки и столбцы;

• ранг матрицы не изменится при ее транспонировании;

• элементарные преобразования матрицы не меняют ее ранга

Определение: Квадратная матрица A^-1 порядка n называется обратной к матрице A, если выполняется условие A^-1A=AA^-1=E, где E - единичная матрица n-го порядка.

Матрица называется вырожденной, если ее определитель равен нулю. Иначе матрица называется невырожденной

Теорема: Для того, чтобы у матрицы A сущестовала обратная матрица, необходимо и достаточно, чтобы исходная матрица была невырожденной

11. Система линейных уравнений. Однородные системы

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.

Здесь   — количество уравнений, а   — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁,a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.