6. Двійкова арифметика

У позиційній системі числення з основою m будь-яке ціле невідємне число a записується послідовністю різних цифр x₁ x_2...x_n, що означає

.

Десяткова система числення використовує цифри 1,2,3,…,9. У цій системі число можна записати таким чином:

2907=210³+910²+110+710⁰.

Для двійкової системи числення достатньо двох цифр 0 та 1. Послідовність цифр x₁ x_2...x_n є записом двійкового n-розрядного числа .

Переведення цілих десяткових чисел у двійкові здійснюється послідовним діленням вихідного числа й кожної частки від ділення на два. Одержані при цьому залишки (0 та 1) і записані в зворотному порядку дають заявлення десяткового числа у двійковій системі числення.

Приклад 1. 26/2=13/2=6/2=3/2=1/2=0

26 12 6 2 0

0 1 0 1 1



26₁₀=11010₂

Перевірка: 12⁴+12³+02²+12¹+02⁰=16+8+2=26.

Дробове число переводиться у двійкову систему методом послідовного множення на 2. При цьому кожного разу після коми двійкового числа записується 0 або 1 відповідно до цілої частини результату множення. Послідовне множення продовжується до тих пір, поки дробова частина не перетвориться в 0 або поки не одержимо потрібну кількість двійкових знаків після коми.

Приклад 2. Представимо у двійковій системі число 0,3125.

0,31252= ,62502= ,25002= ,50002= ,0000.

0 1 0 1

0,3125₁₀=0,0101₂.

Перевірка: 02^-1+12^-2+02^-3+12^-4=1/4+1/16=5/16=0,3125.

Якщо число є змішаним, тобто ціла та дробова частини відрізняються від 0, то вони переводяться в двійкову систему окремо: ціла частина — послідовним діленням, а дробова – послідовним множенням.

Арифметичні операції над числами зводяться до операцій складання і множення однорозрядних чисел. У двійковій системі числення множення задається таблицею кон’юнкції

00=0; 10=0; 01=0; 11=1.

Додавання виконується за правилом

0+0=0; 1+0=0; 0+1=1; 1+1=10 (10 – двійкове число, що відповідає десятковому числу 2).

Приклад 3. 41+27=68 відповідно 101001+11011=1000100.

Приклад 4. 415=205 відповідно 101001101=11001101.

7. Аналіз систем на основі математичної логіки

Нечітка логіка (fuzzy logic) – це математична наука, яка є розширенням

класичної (бульової) логіки й основана на концепції часткової правди – правди, що знаходиться десь посередині між “і” та “немає”. Творець теоретичних основ нечіткої логіки Лотфи-заде (Lotfi Zaden) неодноразово підкреслював, що теорія нечітких висловлень не повинна трактуватись як самостійна, відособлена галузь знань. У деякому аспекті вона служить методологічним розширенням будь-якої іншої специфічної теорії, отриманої шляхом розмивання (fuzzification) її базисних об’єктів (наприклад, чисел), – їхнім перекладом із дискретного стану в безупинне. У наші дні дослідження проводяться, зокрема в області нечітких обчислень (fuzzy calculations), нечітких диференціальних рівнянь (fuzzy differential equations) та ін.

Безпосереднє використання алгоритмів нечіткої логіки в додатках – справа поки досить рідкісна. Втім, очевидною областю впровадження є всілякі експертні системи, у тому числі:

• нелінійний контроль за процесами (виробництво);

• системи, які самонавчаються, названі також класифікаторами (classifiers), дослідження ризикових і критичних ситуацій. У цій області особливо цінується спроможність системи з нечіткою логікою одночасно вдосконалювати декілька каналів узагальнення правил, що помітно відрізняє цей підхід від систем штучного інтелекту, по черзі охоплюючих одну закономірність за іншою;

• розпізнавання образів;

• фінансовий аналіз (ринки цінних паперів);

• дослідження даних (корпоративні сховища);

• удосконалення стратегій керування й координації дій, наприклад складне промислове виробництво.

Нечітка логіка застосовується також при створенні систем підтримки прийняття рішень фінансового аналізу.

Контрольні запитання

1. Дати поняття булевої змінної.

2. Назвати основні функції двозначної логіки.

3. Назвати основні закони булевої алгебри.

4. Назвати операції в алгебрі висловлень.

5. Дати визначення предиката, навести приклади.

Лекція 3

Синтез систем на основні поняття теорії графів

1. Походження графів.

2. Типи скінченних графів.

3. Орієнтовані графи, зважені графи.

4. Суміжність, інцидентність графів, ізоморфізм графів.

5. Маршрути, цикли графів.

6. Планарність графів.

1. Походження графів

Багато задач зводяться до розгляду сукупності об’єктів, суттєві властивості яких описуються зв’язками між ними. Наприклад, дивлячись на карту автомобільних доріг, можна цікавитися лише тим, чи існують зв’язки між деякими населеними пунктами, не звертаючи увагу на конфігурацію доріг, відстані й інші подробиці. При вивченні електричних ланцюгів на перший план може виступати характер з’єднань різних його компонентів: резисторів, конденсаторів, джерел тощо. Органічні молекули утворюють структури, характерними властивостями котрих є зв’язки між атомами. Інтерес можуть викликати різні зв’язки між людьми, подіями, станами і взагалі між будь-якими об’єктами. У подібних випадках зручно розглядати об’єкти точками, так називаними вершинами, а зв’язки між ними – лініями (довільної конфігурації), так називаними ребрами.

Множина вершин V, зв’язки між котрими визначаються множиною ребер E, називається графом G=(V,E).

Граф G задається множиною точок або вершин x₁, x₂,….., x_n , що й позначаються через V, і множиною ліній чи ребер e₁, e₂,….., e_n, які позначаються через E та з’єднують між собою всі або частину цих точок. Отже, граф являє собою пару G=(V, E) множин. Ми завжди будемо мати на увазі, що V E=ø. Зазвичай, граф являє собою креслення, котре складається з точок (вершин) і ліній (ребер), що з’єднують відповідні дві вершини (рис. 3.1.1).

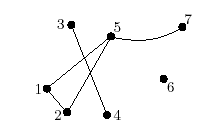
Рис. 3.1.1. Граф на V={1,…,7} з множиною ребер

E={{1,2}, {1,5}, {2,5}, {3,4}, {5,7}.

Множину вершин графа G позначають як V(G), а множину ребер – як E(G).

Кількість вершин графа називають його порядком і записують як |G|, кількість його ребер позначають як ||G||. Графи є обмеженими або не обмеженими відповідно до їх порядку. Граф порядку 0 або 1 називаємо тривіальним.

Перша робота щодо графів була опублікована двадцятирічним Леонардом Ейлером у 1736 році, коли він працював у Російській академії наук. Вона містила розв’язок задачі про кенінгсберзькі мости: чи можна здійснити прогулянку таким чином, щоб, вийшовши з будь-якого місця міста, повернутися на нього, пройшовши у точності лише один раз по кожному мосту? За умовою не має значення, як проходить шлях по частинах суші a,b,c,d, на котрих розміщено м. Кенінгсберг, тому їх можна представити вершинами. А так звані зв’язки між цими частинами здійснюються лише через сім мостів, але кожний із них зображується у вигляді ребра, що з’єднує відповідні вершини. У результаті одержуємо граф (рис. 3.1.2).

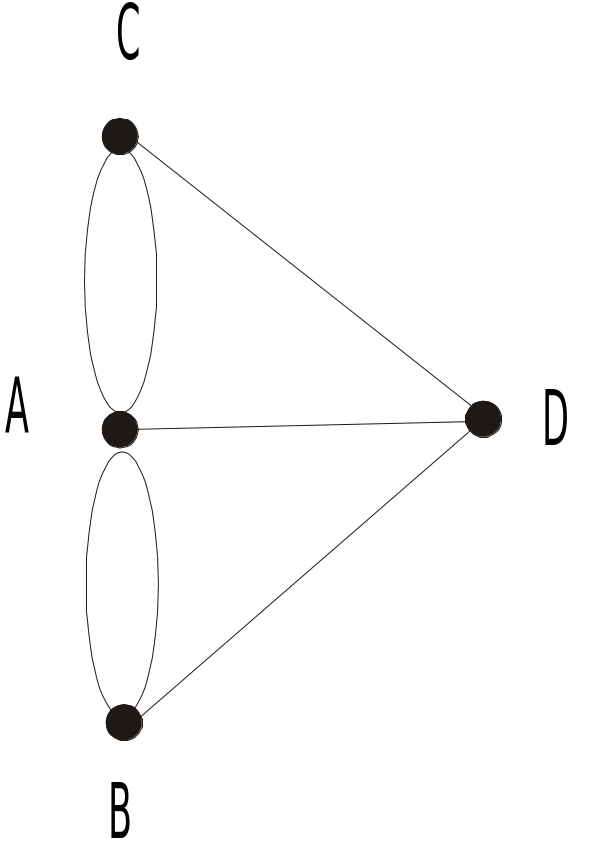
Рис. 3.1.2. Граф до задачі про кенінгсберзькі мости

Ейлер дав заперечну відповідь на поставлене питання. Більше того, він довів, що подібний маршрут існує лише для такого графа, кожна з вершин якого пов’язана з парним числом ребер. Але існує велика кількість задач із застосуванням графів, у яких розглядалися б важливі практичні проблеми, багато з них потребувало тонких математичних методів. Уже у XIX ст. Кірхгоф застосував графи для аналізу електричних ланцюгів, а Келі дослідив важливий клас графів для виявлення і перелічення ізомерів насичених вуглеводів. Однак теорія графів як математична дисципліна сформувалася лише у середині 30-их років XX ст. завдяки роботам таких дослідників, як Кенінг, Понтрягін, Зиков, Візинг. Теорія графів має потужний апарат розв’язання прикладних задач із найрізноманітніших галузей науки й техніки. Наприклад, аналіз та синтез ланцюгів і систем, проектування каналів зв’язку й дослідження процесів передачі інформації, побудова контактних схем і вивчення кінцевих автоматів, планування мереж та їх управління, дослідження операцій, вибір оптимальних маршрутів і потоків у мережах, моделювання нервової системи у живих організмів та багато інших задач. Теорія графів тісно пов’язана з такими розділами математики, як теорія множин, математична логіка, теорія ймовірностей.

Нехай маємо два графи G і G. Вважаемо, що та .

Якщо =, тоді G і G не перетинаються. Якщо та , то G є підграфом графа G (граф G – надграфом для G^’). У цьому випадкові записуємо , формально ми говоримо, що граф G містить граф G (рис. 3.1.3).

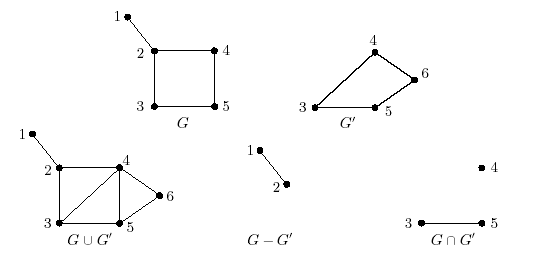
Рис. 3.1.3. Об’єднання, перетин, різниця графів G та G

Якщо містить усі ребра xy E x,y V, то G  індукований підграф у G.