Контрольні запитання

1. Що являє собою модель? Які існують класи моделей?

2. Що називається моделюванням?

3. Які ви можете назвати задачі оптимального керування?

4. У чому полягає геометричний зміст задач лінійного програмування?

5. Що являє собою цільова функція?

6. У якому випадку задача лінійного програмування має оптимальний розвязок?

7. Що являє собою математична модель задачі лінійного програмування?

Лекція 8 Поняття про складні системи керування

1. Умови існування системи керування.

2. Види зв’язків у системах керування.

3. Види керування.

4. Економічна система, її загальна характеристика.

5. Системний підхід при дослідженні економічної системи.

6. Економічна система як система керування.

1. Умови існування системи керування

Наявність керування є суттєвою ознакою складної системи, що забезпечує її цілісність.

Керування – це цілеспрямований вплив однієї системи на іншу для зміни її поведінки (стану) відповідно до зміни умов зовнішнього середовища.

Поняття керування є базовим поняттям у кібернетиці, оскільки визначає предмет дослідження цієї науки. Будь-яку систему, що є об’єктом кібернетичного дослідження можна представити у вигляді системи керування.

Системою керування називається організаційна динамічна система з оберненим звязком, у якій реалізуються причинові зв’язки за допомогою двох каналів.

Розглянемо схему реалізації системи керування (рис. 8.1.1).

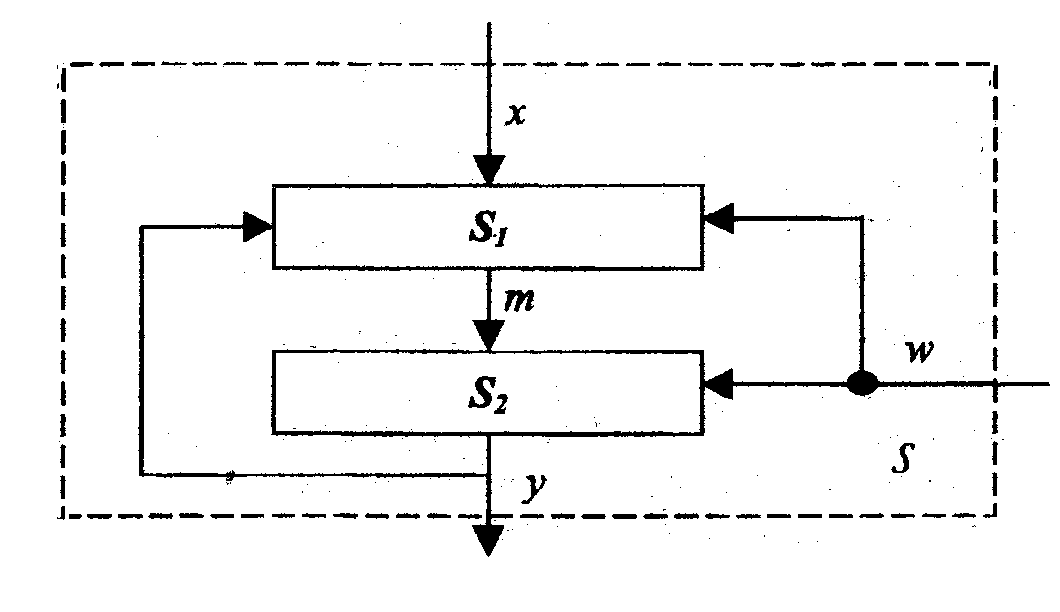
Рис. 8.1.1. Схема системи керування

Нехай x характеризує вхід, що визначає мету функціонування системи керування S. Керуюча система S₁ виробляє керувальну дію m, що передається на вхід управляючої системи S₂.

На систему S впливає збуджувальна дія w. Результати роботи системи y по каналу оберненого зв’язку надходять на вхід S₁, аналізуються і використовуються для оброблення наступних керуючих впливів.

Головними умовами існування системи керування є:

1. організованість: у системі керування виділяються елементи, що належать або до керуючих, або до тих, якими керують, або до керуючої підсистеми: S = S₁S₂;

2. різноманітність: кожна з двох виділених підсистем повинна допускати можливість появи декількох (багатьох) станів.

2. Види зв’язків у системах керування

Вид з’єднання елементів, при котрому вихідна дія одного елемента передається на вхід другого елемента, називається прямим зв’язком. Прямий зв’язок між двома елементами системи може здійснюватися безпосередньо чи через інші її елементи.

Вид з’єднання елементів, при якому вихідна дія одного елемента передається на вхід того самого елемента, називається оберненим зв’язком. Обернений зв’язок може здійснюватися або безпосередньо від виходу елемента системи на його вхід, або через інші елементи цієї системи. Обернений зв’язок буває зовнішнім та внутрішнім.

Зовнішнім, або головним, називається такий зв’язок за допомогою котрого здійснюється передача частини вихідного сигналу всієї системи керування на її вхід.

Внутрішні, або місцеві, обернені зв’язки з’єднують вихід окремих елементів чи груп послідовно з’єднаних елементів із їх входом.

Розрізняють додатний і від’ємний обернений зв’язок. Додатний обернений зв’язок підсилює дію вхідного сигналу, від’ємний – послаблює. Додатний обернений зв’язок використовується у багатьох технічних пристроях для збільшення коефіцієнта передачі. В економіці на принципі додатного оберненого зв’язку засновані системи матеріального стимулювання. Прикладом використання від’ємного оберненого зв’язку є термостат. Цей вид зв’язку допомагає встановленню рівноваги системи.

Обернений зв’язок відіграє важливу роль при розпізнаванні образів і прийнятті рішень. В організаційних системах обернені звязки використовують для вироблення керуючих сигналів, критерію ефективності керування й оцінювання його якості. У біологічних системах обернені зв’язки підтримують у нормальному стані основні показники життєдіяльності: температуру, масу тіла, рівень цукру, гемоглобіну в крові та ін.