2. Логічні операції над множинами та їх властивості. Тотожні перетворення виразів
Множину можна також визначити за допомогою операцій над іншими множинами. Нехай маємо дві множини А і В.
Об’єднання (сума) А В є множина всіх елементів, що належать А та В.
Наприклад, {1, 2, 3} {2, 3, 4} = {1, 2, 3, 4}.
Для наочного зображення співвідношень між множинами будь-якого універсума U використовують круги Ейлера. Зазвичай універсум подають множиною точок прямокутника, а його підмножини зображають у вигляді кругів або інших простих областей усередині цього прямокутника. Об’єднання зображується таким чином (рис. 1.2.1):
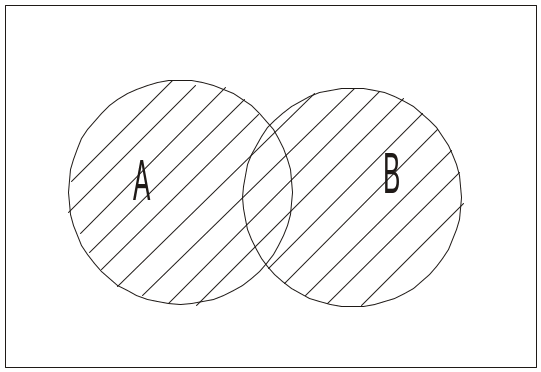
Рис. 1.2.1. Об’єднання (сума) А В
Перетин (добуток) А В є множиною всіх елементів, що належать одночасно як А, так і В (рис. 1.2.2).
Наприклад, {1, 2, 3} {2, 3, 4} = {2, 3}.
Рис. 1.2.2. Перетин (добуток) А В
Множини, які не мають спільних елементів, називаються різночленними або неперетинаючими А В = (рис. 2.3).
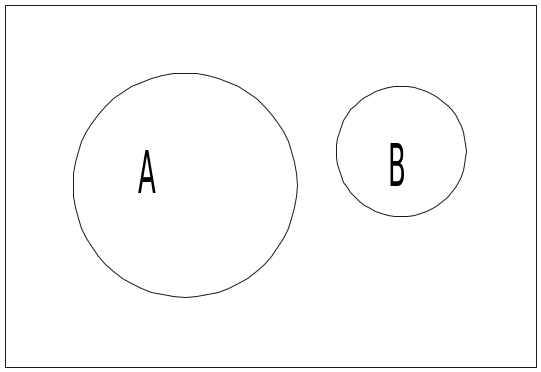
Рис. 1.2.3. Перетин (добуток) А В=
Різниця А \ В (чи А - В ) є множиною, котра складається з усіх елементів А, що не входять у В (рис. 1.2.4).
Наприклад, {1, 2, 3} \ {2, 3, 4} = {1}.
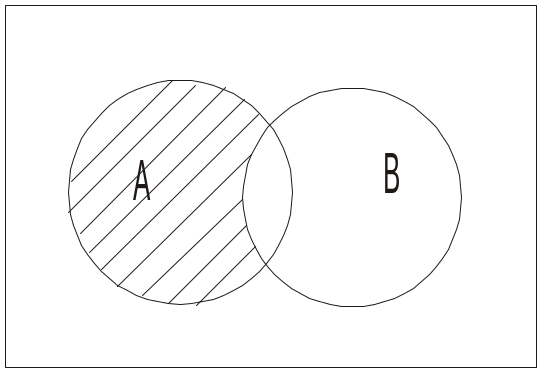
Рис. 1.2.4. Різниця А \ В
Її можна
розглядати як відносне доповнення В
до А.
Якщо
А
В,
то множина U\A
називається
абсолютним доповненням (або просто
доповненням) множини A
і
позначається через
.
Вона містить усі елементи універсума
U,
крім елементів множини А
(рис. 1.2.5).
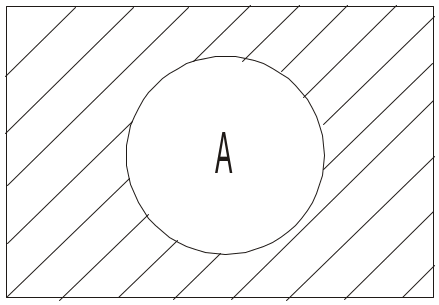
Рис. 1.2.5. Доповнення
Доповнення
А
визначається
запереченням властивості P(x),
за допомогою якої визначається А.
Очевидно, А
\ В
= А
(рис. 1.2.6).
Рис. 1.2.6. Різниця А \ В = А , при А В
Диз’юктивна сума (симетрична різниця) А+В (чи АВ) є множиною всіх елементів, що належать або А або В (але не обом одразу)(рис. 1.2.7).
Наприклад, {1, 2, 3} + {2, 3, 4} = {1, 4}.
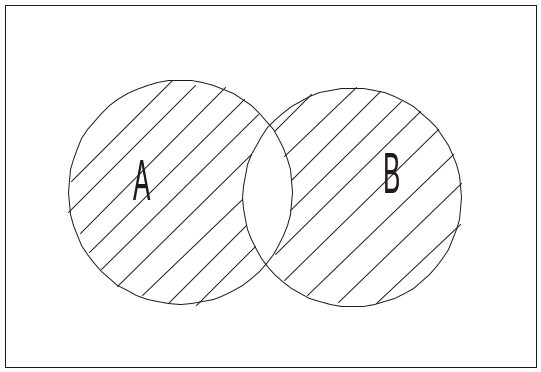
Рис. 1.2.7. Сума А + В
Диз’юктивну суму одержуємо об’єднанням елементів множин, за винятком тих, які трапляються двічі.
Властивості операцій над множинами.
Комутативний закон для об’єднання і перетину множин
А В= В А;
А В= В А.
Асоціативний закон для об’єднання та перетину множин
А (В С)=(А В) С;
А (В С)=(А В) С.
Дистрибутивний закон для об’єднання і перетину множин
А (В С)=(А В) (А С);
А (В С)=(А В)(А С).
Властивості пустої множини та універсума відносно об’єднання
А = А;
А
=
U;
А U = U;
=U.
Властивості пустої множини та універсума відносно перетину
А U = A;
А = ;
А = А;
=.
Закон ідемпотентності для об’єднання і перетину множин
А А = А;
А А = А.
Закон поглинання
А ( А В) = А;
А ( А В) = А.
Теорема де Моргана
;
.
Наступні властивості:
Якщо А В = U і А В =, то В= ;
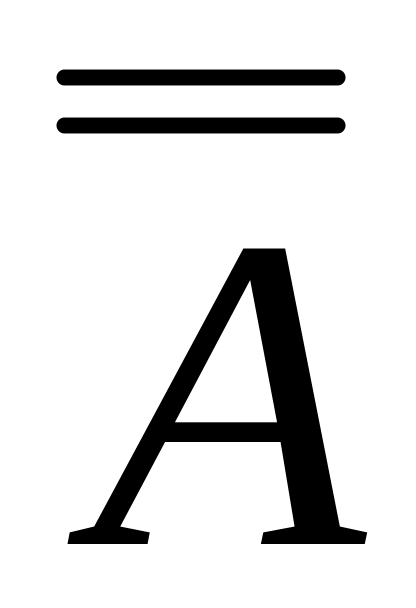=U \ А;
=А;А \ В=А В;
А+В =(А
)(
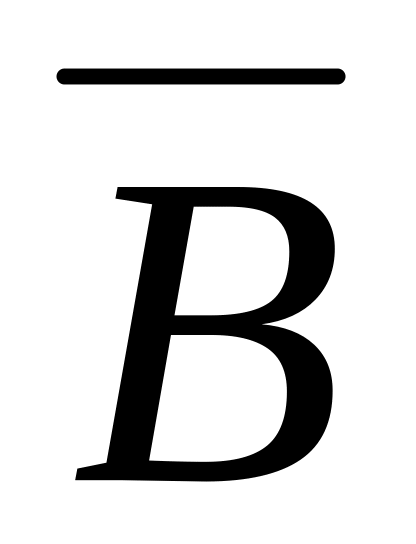В);А+В =В+А;
А+В+С =А +(В+С);
А+ =+А = А;
А В, тоді й тільки тоді, якщо А В=А, або А В=В, або А =;
А=В, тоді та тільки тоді, якщо (А )( В)=.
Ми розглядали операції над множинами і їх властивості (закони операцій). Усі ці закони можна довести. Є різні способи доведення.
1. Доведення цих тотожностей за допомогою відношення належності
Приклад. Довести дистрибутивний закон А (В С)=(А В) (А С) .
Доведення
Уважатимемо, що xА (В С), тоді xА або x(В С). Якщо xА, то x належить об’єднанню з А з будь-якою множиною, тобто xА В і xА С ; із цього слідує, що x є елементом перетину множин А В і А С, тобто x(А В) (А С).
Якщо xВ С, то xВ і xС, а значить, xА В і xА С, тобто x є елементом перетину тих же множин. Таким чином, доведено, що
А (В С)(А В) (А С).
Аналогічно доводимо і відношення
А (В С)(А В) (А С).
Згідно з визначенням рівності множин маємо потрібну тотожність
А (В С)=(А В) (А С).
2. Доведення тотожностей за допомогою кругів Ейлера
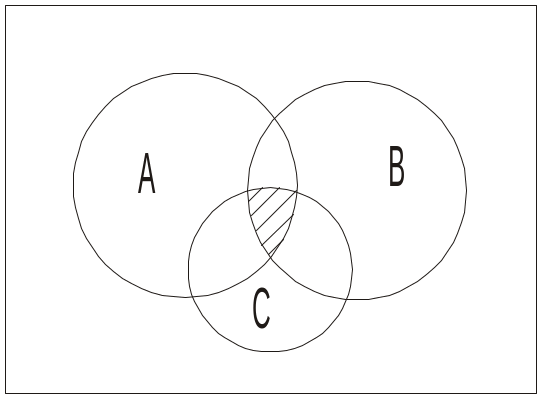
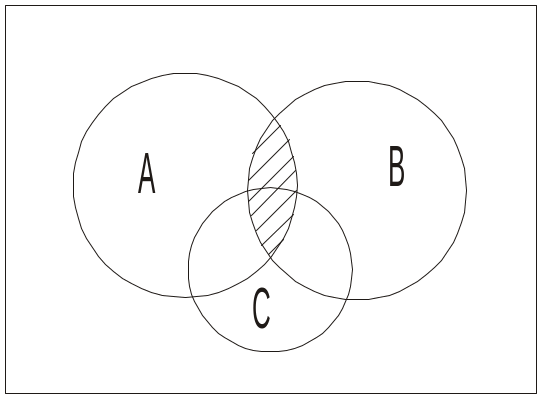
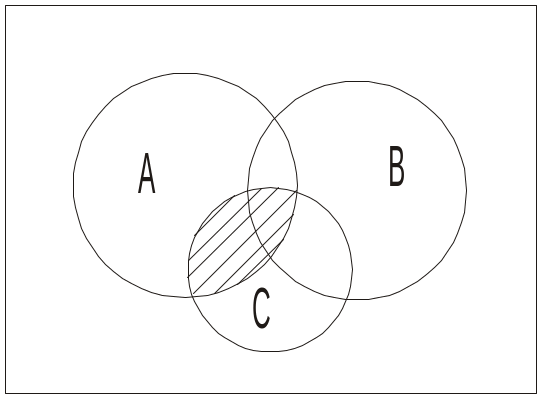
Приклад. Довести дистрибутивний закон А (В С)=(А В) (А С) за допомогою кругів Ейлера.
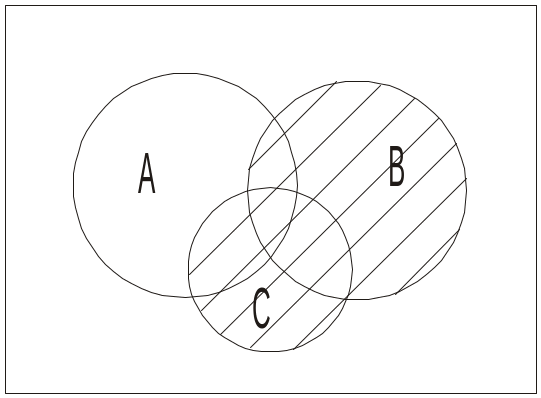
Доведення. Проілюструємо за допомогою кругів Ейлера спочатку ліву частину тотожності, виконавши спочатку об’єднання множин В і С, а потім перетин з А. Потім побудуємо діаграму для правої частини тотожності (рис. 1.2.8).
Рис. 1.2.8. Доведення тотожності А (В С)=(А В) (А С) за допомогою кругів Ейлера
Як бачимо, діаграми збігаються, отже, тотожність доведена.
За допомогою тотожних перетворень
Приклад. Довести, що А А = А.
Доведення
А А =(А А) U= (А А) (А )= А ( А ) = А = А.
З комутативності та асоціативності операцій об’єднання слідує, що об’єднання декількох множин можна виконати послідовно, об’єднуючи ці множини, причому порядок слідування множин не впливає на результат. Так, для множин А, В, С можна записати А В С=(А В) С=(В С)А.
Отже, сукупність множин можна позначити відношенням
.
Теж саме можна записати і для перетину сукупності множин
.
Тотожні перетворення. Алгебра множин являє собою теоретико-множинний аналог звичайної алгебри дійсних чисел та основана на властивостях операцій над множинами. За допомогою тотожних перетворень можна спрощувати або перетворювати у зручний вигляд вирази, що містять множини, при цьому застосовують властивості операцій.
Приклад 1. Виконати тотожні перетворення.
Приклад 2
.