4. Аналіз скінченних автоматів

Повний опис поведінки автоматів полягає у визначенні вихідних сигналів при збудженні його у тактові моменти часу деякою послідовністю вхідних сигналів. Вхідна та вихідна послідовності представляються наборами символів (або їх номерами) із X , Y. Для такого опису необхідно визначати і задавати ще й початковий стан автомата.

Найбільш зручно визначати реакцію автомата на вхідну послідовність за його графом. Для цього лише потрібно простежити шлях у графі, починаючи від вершини початкового стану по направленню дуг, які відмічені наступними номерами із вхідної послідовності. Вихідна послідовність визначається номерами, котрими відмічені дуги у порядку їх слідування по пройденому шляху, а послідовність станів автомата – номерами вершин, через які проходить цей шлях.

Приклад

Нехай маємо початковий стан 0 і вхідну послідовність (2, 0, 1, 1, 2, 3) . Тоді визначаємо зміну станів автомата (1, 3, 0, 2, 2, 3) та відповідно вихідну послідовність (0, 1, 0, 0, 1, 1). При початковому стані 2 й при тій же вхідній послідовності одержимо відповідно зміну станів (2, 3, 0, 2, 2, 3) та відповідно вихідну послідовність (1, 1, 0, 0, 1, 1).

За допомогою графа автомата легко виділити такі характерні типи його станів:

1. перехідний стан, із котрого можна перейти принаймні в один інший стан, але після цього вже не можна повернутися у нього ні при якій дії (відповідна вершина не має вхідних дуг, але має хоча б одну вихідну дугу);

2. тупиковий стан, у котрий можна перейти принаймні з одного до іншого стану, але після цього вже не можна вийти з нього ні при якій дії (відповідна вершина не має вихідних дуг в інші вершини, але має принаймні хоч одну дугу з іншої вершини);

3. ізольований стан, із якого не можна перейти в жодний інший стан і в нього не можна потрапити ні з якого іншого стану (відповідна вершина містить лише петлю).

Аналогічні визначення можна дати для деяких сукупностей станів, що розглядаються як підавтомати. Нехай М1, М2, М3 – відповідно перехідний, тупиковий та ізольований підавтомати автомата М, які характеризуються множиною станів S1, S2, S3. Очевидно, виділення таких підавтоматів відповідає розбиттю множини S станів автомата M на неперетинаючі підмножини S1, S2, S3 (рис. 5.4.1).

S1 S2 S3 = S;

S1 S2 S3 = .

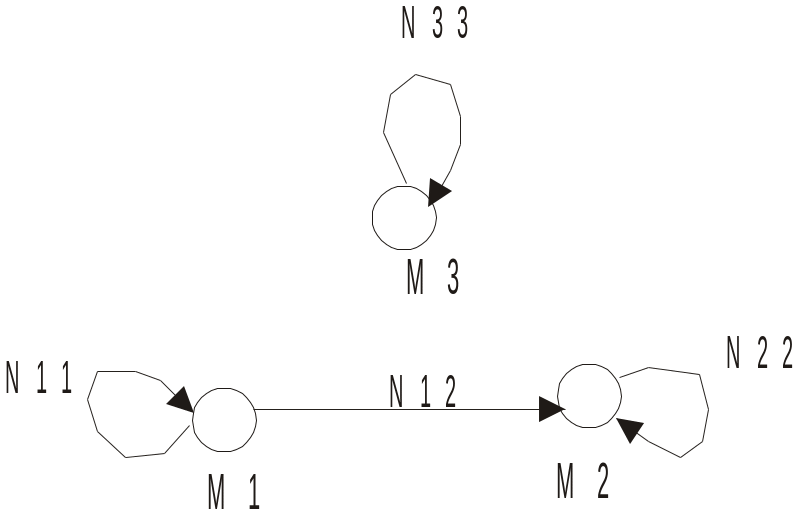
Рис. 5.4.1. Множина неперетинаючих станів автомата M

Матриця відповідного графа може бути представлена у вигляді

.

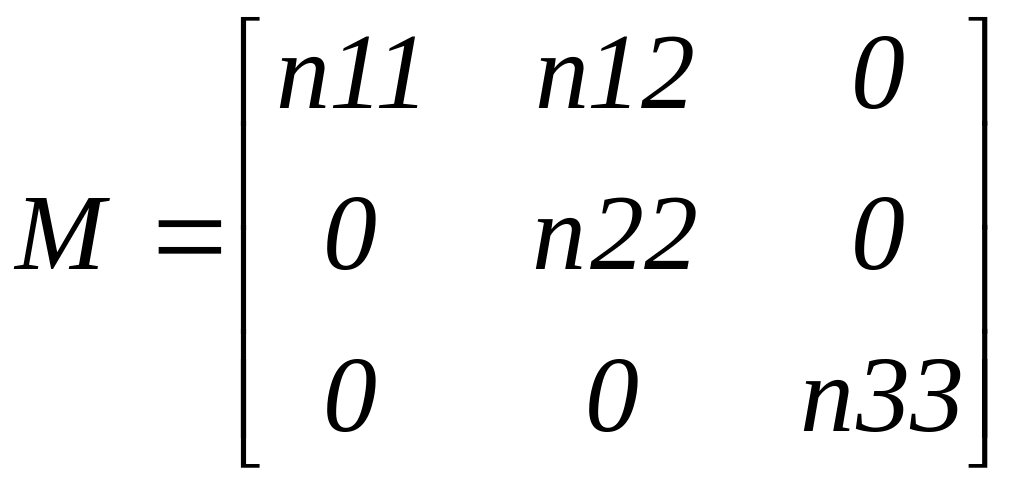5. Автомати Мілі та Мура

Скінчеyнний автомат, у котрому вихідна інформація поставлена у відповідність переходам, називається автоматом Мілі.

Скінченний автомат, у якому вихідна інформація поставлена у відповідність станам, називається автоматом Мура.

Це означає, що в автоматах Мілі функція виходів – це залежність вихідної інформації від поточного стану і поточної вхідної інформації, а в автоматах Мура функція виходів – це залежність вихідної інформації тільки від поточного стану. Розглянемо приклад автомата Мілі.

Приклад 1

Побудувати скінченний автомат, який здійснює додавання двох натуральних чисел, використовуючи їх бінарне зображення.

Пояснимо процедуру порозрядного бінарного додавання. Нехай є два числа, записані за допомогою n-розрядного війкового коду: і . Спочатку додаються та , у результаті чого виходить результат та перенесення . Після цього робиться додавання , та , у результаті виходить й перенесення . Ця процедура продовжується до кроку n , на якому при додаванні , та і виходить та . Остання сума дорівнює перенесенню .

_____________

Перенесення

Скінченний автомат, що виконує це додавання, можна побудувати , використовуючи тільки два стани.

Розглянутий автомат має множину станів , множину вхідних символів , множину вихідних символів , початковий стан – . Будемо вважати, що автомат припиняє роботу, коли закінчилося надходження вхідних даних. Це означає, що додавання завершено.

Вхідними даними на одному такті є два біти – відповідні біти доданків, тому можливі варіанти вхідної інформації для одного такту – . Переходи побудовані відповідно до одержуваної суми, яка зображена вихідним бітом, і перенесенням, котре зображене станом ( – перенесення дорівнює 0, – перенесення дорівнює 1).

Відображення (функція переходів) та (функція виходів) наведені у таблиці 6.5.1. У таблиці зображено, що коли біти, які додаються, 00 і поточний стан (перенесення немає), то автомат залишається у стані (перенесення немає) та видає результат 0. Якщо біти, котрі додаються, – 00 і поточний стан (перенесення – 1), то автомат залишається у стані (перенесення немає) та видає результат 1. Якщо біти, які додаються, – 10 і поточний стан (перенесення – 1), то автомат залишається у стані (перенесення – 1) та видає результат 0.

Таблиця 5.5.1

Таблиця станів автомата

Стани
		00	01	10	11	00	01	10	11