5. Нечіткі відношення

Нехай – прямий добуток множин та – його множина належності; нечітке -арне відношення визначається як нечітка підмножина , що приймає свої значення в . Нечітке відношення в запишеться як

Використаємо наступні символи: – позначення максимуму відносно елемента або змінної ; – позначення мінімуму відносно елемента або змінної .

Так, запис еквівалентний . Запис еквівалентний .

Першу проекцію нечіткого відношення визначає функція належності . Аналогічно другу проекцію нечіткого відношення визначає функція належності .

Друга проекція першої проекції (або навпаки) називається глобальною проекцією нечіткого відношення і позначається . Таким чином, .

Якщо , то говорять, що відношення нормальне. Якщо , то відношення субнормальне.

Нехай та – два нечітких відношення, такі, що , тоді говорять, що .

Об’єднання двох відношень та позначається або і визначається виразом

Якщо – відношення, то . Результат об’єднання позначається або .

Перетин двох відношень та позначається і визначається виразом

Нехай – нечітке відношення. Звичайне відношення, найближче до , визначається виразом

Контрольні запитання

1. Як повязані теорія відношень та теорія множин?

2. Що називається відношенням? Назвіть способи задавання відношення.

3. Що являє тотожне відношення, повне відношення, порожнє відношення?

4. Як одержати граф відношення, оберненого до даного?

5. Чи може відношення мати не одну, а кілька властивостей?

6. Дати визначення несіткого відношення.

7. Що являє собою перша та друга, глобальна проекції нечіткого відношення?

8. Що являє собою об’єднання двох нечітких відношень?

Лекція 5 Синтез систем на основі поняття про теорію автоматів

1. Загальна характеристика автоматів.

2. Скінченні автомати.

3. Представлення скінченних автоматів.

4. Аналіз кінцевих автоматів.

5. Автомати Мілі та Мура.

1. Загальна характеристика автоматів

У техніці з поняттям автомата, як правило, пов’язують деякий прилад, здатний виконувати визначені функції без утручання людини або з її обмеженою участю.

Однак таке поняття є дуже вузьким. У широкому розумінні кінцевий автомат – це математична модель, що відображає фізичні та абстрактні явища найрізноманітнішої природи.

Така модель успішно використовується як у техніці (проектування обчислювальних машин, систем управління й звязку), так і в інших галузях – психології та фізіології (дослідження діяльності нервової системи людини і найпростіших видів поведінки тварин), лінгвістиці (аналіз синтаксису різних мов, розшифрування стародавніх рукописів), теорії та практиці адміністративного управління.

Автомат – це схематизований алгоритм. Обчислення за алгоритмом можна розглядати як деякий процес, котрий описується своєю множиною станів, початковим станом і правилами переходу від стану до стану. Універсальність теорії автоматів дозволяє розглядати з єдиної точки зору різні об’єкти, встановлювати зв’язки й аналоги між ними переносити результати з однієї області в іншу.

Автомат можна зобразити у вигляді схеми (рис. 5.1.1).

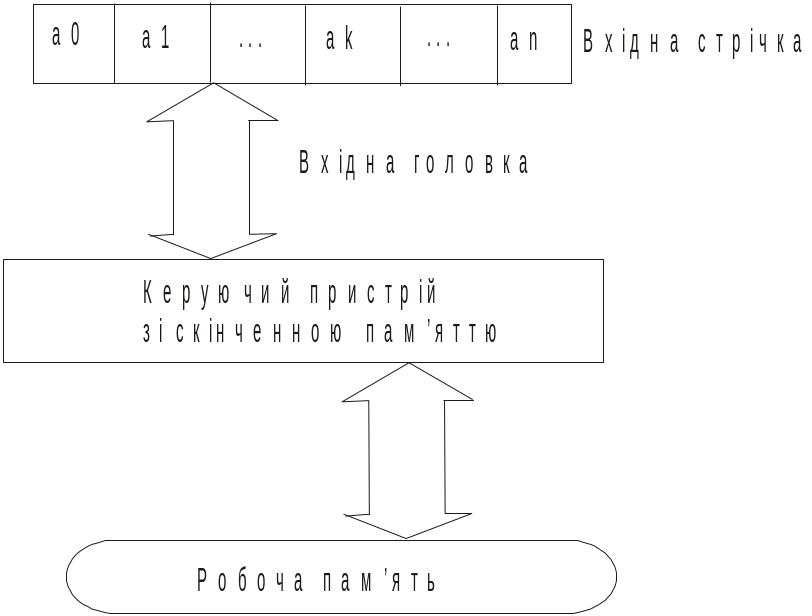
Рис. 5.1.1. Схема автомата

Автомат складається з трьох частин: вхідної стрічки, керуючого пристрою зі скінченною пам’яттю і допоміжної або робочої пам’яті.

Вхідну стрічку можна розглядати як лінійну послідовність клітинок, чи комірок, причому кожна комірка містить точно один вхідний символ із деякого скінченного вхідного алфавіту. Ліву і праву комірки можуть займати особливі кінцеві маркери, позначимо їх . Порожні комірки позначаємо . За допомогою вхідної стрічки зображується інформація, що надходить на вхід автомата.

Вхідна головка у кожний момент читає одну вхідну комірку. За один крок роботи автомата вхідна головка може зміститися на одну комірку вліво, залишитися нерухомою або зміститися на одну комірку вправо. Автомат, який ніколи не переміщує свою вхідну головку вліво, називається одностороннім. Схему вхідної стрічки та вхідної головки зображено на рисунку 5.1.2.

Вхідна головка може бути тільки такою, котра читає, якщо під час роботи автомат не утворює рядок – результат. Існують такі автомати, вхідна головка котрих виконує функції читання і написання. Такі автомати можуть записувати результуючий рядок чи змінювати символи на вхідній стрічці.

Рис. 5.1.2. Вхідна стрічка та вхідна головка

Пам’ять автомата – це структура, в якій записуються, зберігаються і зчитуються додаткові дані, що використовуються автоматом при роботі. Для кожного виду автоматів строго визначено тип памяті, функції доступу до пам’яті та перетворення пам’яті. Автомат може не мати пам’яті. Тип пам’яті часто визначає назву автомата.

Робота автомата складається з послідовності тактів. Кожний такт складається з послідовності таких дій:

1. Читається поточний вхідний символ.

2. За допомогою функції доступу досліджується память, і до неї заноситься деяка інформація.

3. Змінюється стан керуючого пристрою.

4. Записується вихідна інформація у комірки вхідної стрічки.

5. Вхідна головка зміщується на одну комірку вліво, вправо або зберігається у початковому стані.

Поточний вхідний символ та інформація, витягнута з пам’яті, разом з поточним станом керуючого пристрою визначають, яким повинен бути цей стан.

Таким чином, на кожному такті встановлюється поточна конфігурація автомата, до якої входять:

• поточний стан керуючого пристрою;

• поточний зміст вхідної стрічки;

• поточний зміст робочої пам’яті.

Конфігурація автомата змінюється на кожному такті під впливом керуючого пристрою.

Керуючий пристрій складається зі скінченної множини станів і відображень, які залежно від попередньої конфігурації дозволяють визначити нову конфігурацію автомата, напрям переміщення вхідної головки (якщо вона не одностороння), інформацію на друку (якщо в автоматі передбачено функцію друку), інформацію, що заносять у пам’ять та витягують із пам’яті (якщо автомат має робочу пам’ять).

Автомат починає роботу з початкової конфігурації. При початковій конфігурації керуючий пристрій знаходиться в заданому початковому стані, вхідна голівка оглядає лівий символ на вхідній стрічці, й пам’ять має заздалегідь установлений початковий зміст. Конфігурація, при якій автомат припиняє роботу, називається завершальною. Автомат припиняє роботу, перейшовши в один із станів заздалегідь виділеної множини завершальних станів, або тоді, коли перегляд вхідних даних завершальною. Умови припинення роботи чітко визначаються для кожного конкретного автомата.

Керуючий пристрій є не детермінованим, якщо для кожної конфігурації існує скінченна множина можливих конфігурацій (більше від однієї), так що в будь-яку з них автомат може перейти на наступному кроці. Керуючий пристрій називається детермінованим, якщо для кожної конфігурації існує не більше від однієї можливої наступної конфігурації. Відповідно автомат називається детермінованим і недетермінованим залежно від виду керуючого пристрою.