4. Суміжність, інцидентність графів, ізоморфізм графів

Дві вершини v_i, v_j  V графа G=(V,E) називаються суміжними, якщо вони є граничними вершинами ребра e_kE. Відношення суміжності на множині вершин графа можна визначити, представивши кожне ребро як пару суміжних ребер e_k=(v_i, v_j), k=1,2,…,q. Для неорієнтованих графів такі пари невпорядковані. Граф можна представити матрицею суміжності. Рядки і стовпці матриці відповідатимуть вершинам графа, її (i,j) елемент дорівнює кількості кратних ребер, що зв’язують вершини v_i, v_j . Наприклад, для графа (рис. 3.3.1) маємо

v1	v2	v3	v4	v5
	1				v1
1		2		1	v2
	2			1	v3
					v4
	1	1		1	v5

Матриця суміжності неорієнтованого графа завжди симетрична, а орієнтованого, як правило, несиметрична. У стовпцях і рядках відповідно ізольованих вершин усі елементи рівні 0. Елементи матриці простого графа дорівнюють 0 або 1, причому всі елементи головної діагоналі – 0.

Для зваженого графа, що не містить кратних ребер, можна узагальнити матрицю суміжності так, що кожний її ненульовий елемент дорівнює вазі відповідного ребра чи дуги.

Інцидентність графів. Якщо вершина v_i є кінцем ребра e_k, то говорять, що вони інцидентні (вершина інцидентна ребру, ребро інцидентне вершині). У той час як суміжність являє собою відношення між однорідними обєктами (вершинами), інцидентність – відношення між різнорідними обєктами (вершинами і ребрами). Інцидентність для (p, q)-графа можна представити матрицею розміру p q. Для неорієнтованого графа елементи цієї матриці визначаються за таким правилом: (i,j) елемент дорівнює 1, якщо v_i інцидентна ребру e_i, і дорівнює 0, якщо вони не інцидентні. У випадку орграфа дорівнює 1, якщо v_i початкова вершина ребра, й дорівнює (– 1), якщо v_i кінцева вершина, наприклад, інцидентна матриця для графа (рис. 3.3.1).

Кожний стовпець матриці інцидентності містить обов’язково два одиничних елементи. Кількість одиниць у рядку дорівнює степеню відповідної вершини. Нульовий рядок відповідає ізольованій вершині, а нульовий стовпець – петлі.

e1	e2	e3	e4	e5	e6
1						v1
1	1	1	1			v2
	1	1		1		v3
						v4
		1	1			v5

Ізоморфізм графів. Графи, для яких зберігається відношення інцидентності, називаються ізоморфними. Приклад ізоморфних графів наведено на рисунку 3.4.1.

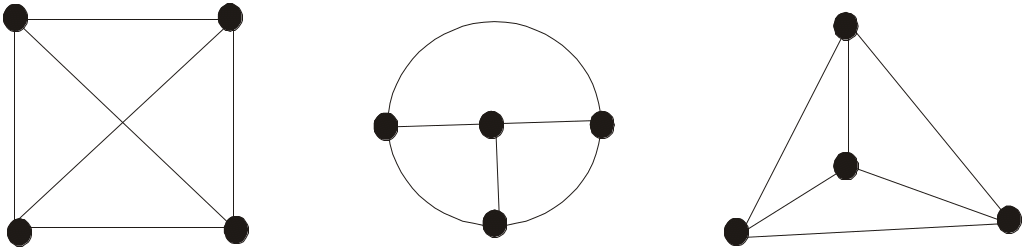
Рис. 3.4.1. Ізоморфні графи.

Графи, які мають однакові накреслення і відрізняються лише нумерацією вершин та ребер, не будучи тотожними, є ізоморфними.