2.5.2 Нахождение индекса согласованности обратно–симметричной матрицы. Задача шкалирования. Столбец приоритетов.

Описываемые ниже способы нахождения ИС ОСМ А являются эффективными лишь для обратно-симметричных матриц, достаточно близких к согласованным. К настоящему времени существуют четыре известных способа. Отметим сразу, что если матрица А является идеальной, то все они приводят к одному и тому же результату. В общем случае это не так.

В качестве численного примера рассмотрим ОСМ 4-го порядка:

(1) (2)

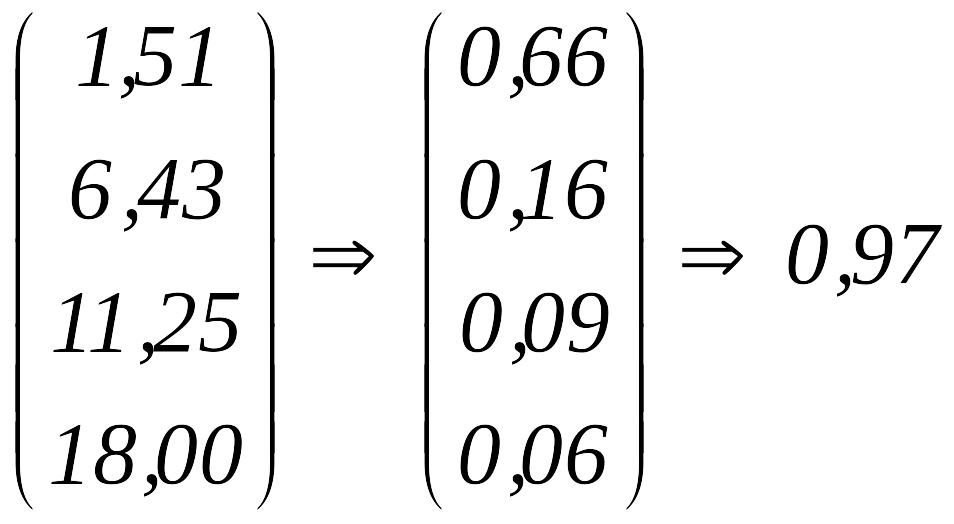
Используем для наглядности второй способ, предложенный Т.Саати. Сначала суммируем элементы каждого столбца (см. результаты (2)). Далее заменяем каждый элемент построенного столбца на обратное число. Складываем элементы столбца из обратных величин. Делим каждый из элементов построенного столбца на полученную сумму 0,97, т.е. . Умножим теперь матрицу А на полученный столбец, имеем . Разделим каждый элемент столбца-произведения на каждый из соответствующих элементов столбца-множителя, получим следующие результаты: 3,59;6,31;2,78;3,50. Найдем их среднее арифметическое: . Это и есть приближенное максимальное собственное значение исходной ОСМ А, т.е . Теперь уже совсем легко найти индекс согласованности (ИС) ОСМ А, который равен: , то есть степень согласованности суждений является удовлетворительной.

При любом подходе к суждениям об эксперименте важное значение имеет выбор шкалы сравнений. Главное требование - шкала сравнений должна быть простой и естественной. Обычно в качестве чисел шкалы берут числа от 1 до 9. Почему?

Способность человека представлена, как правило, пятью определениями для проводимых разграничений: слабо разграничиваются, равные, сильно разграничиваются, очень сильно, абсолютно разграничиваются.

Таблица сравнений. Пусть даны элементы - объекты А, В, С и D…системы S. Таблица сравнений имеет вид:

	A	B	C	D	…
A
B
C
D
…

Она строится по следующим правилам:

1. Если элементы А и В одинаково важны (одинакового уровня), то заносим в позицию (А, В) таблицы сравнений единицу;

2. Если объект А значительно важнее В, то в (А, В) заносим число 5, аналогично 1/5 в (В, А);

3. Если А явно важнее, чем В, то число 7; если А абсолютно важнее, то 9.

Числа 2, 4, 6 и 8 используются для облегчения компромиссов между оценками, слегка отличающимися от основных чисел в таблице сравнений.

ПРИМЕР: предположим, что сравнивая объекты А, B, C и D (цеха предприятия) в системе S (предприятие), мы вынуждены написать следующую таблицу сравнений:

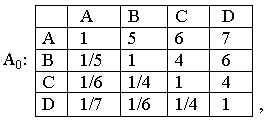
которая приводит к уже рассмотренной нами обратно-симметричной матрице А. Для нее уже был найден индекс согласованности (ИС) с идеальной матрицей сравнений, который оказался равным ИС0,017. Сумма всех элементов полученного столбца-множителя (его еще называют столбцом приоритетов) равна . Он и позволяет подвести итог полученной таблице сравнений .

Среди сравниваемых элементов A, B, C и D (объектов системы S) наивысший приоритет имеет объект А (доля приоритета в системе равна 68%), затем идет объект В (доля приоритета равна 16%), далее идет объект С (доля приоритета равна 9%), наконец, объект D (доля приоритета равна 6%).