1.1. Введение

1.2. Определение эконометрики. Примеры решения эконометрических задач

1.3. Определение слова «спецификация»

1.4. Требования к спецификации эконометрической модели

1.5. Дополнительный материал

1.1. Введение

Приводим основные математические обозначения, формулы, которые будут использованы по курсу эконометрика.

Массив чисел: 10, 15, 19, 21 можно обозначить: х1, х2, х3, х4 или Хi, i = 1, 2, 3, 4

Массив чисел можно представить в разных видах:

- перечислением: х1=10, х2= 15, х3= 19, х4= 21;

- таблицами:

i	Хi
1	10
2	15
3	19
4	21

i	1	2	3	4
Хi	10	15	19	20

Сумма массива чисел - ΣХi = х1+х2+х3+х4 = 10+15+19+21= 65

i	Хi
1	10
2	15
3	19
4	21
Сумма	65

Среднее значение массива чисел: Хс = (ΣХi)/n = (х1+х2+х3+х4)/4 = (10+15+19+21)/4=65/4=16,25,

i	Хi
1	10
2	15
3	19
4	21
Сумма	65
Среднее	16,25

Вариация массива чисел: Σ(Хi-Хс)² = (х1-Хс)² + (х2-Хс)² (х3-Хс)² (х4-Хс)² = (10-16,25)²+(15-16,25)²+(19-16,25)²+(21-16,25)² = 39,06+1,56+7,56+22,56= 70,74

i	Хi	(Хi-Хс)2
1	10	39,06
2	15	1,56
3	19	7,56
4	21	22,56
Сумма	65	70,74
Среднее	16,25

Дисперсия массива чисел: S² = (Σ(Хi-Хс)²)/(n-1)= 70,74/(4-1) = 23,58,

i	Хi	(Хi-Хс)2
1	10	39,06
2	15	1,56
3	19	7,56
4	21	22,56
Сумма	65	70,74
Среднее	16,25
S2		23.58

Среднее квадратическое отклонение массива чисел: S= корень(S²) = корень (23,58) = 4,85

i	Хi	(Хi-Хс)2
1	10	39,06
2	15	1,56
3	19	7,56
4	21	22,56
Сумма	65	70,74
Среднее	16,25
S2		23.58
S		4.85

Х – матрица

	10
Х =	15
	19
	21

Х^т – транспонированная матрица

Хт =

10

15

19

21

Х^тХ – произведение матриц, Х^т – первая матрица, Х – вторая матрица

Х^тХ = 10*10+15*15+19+19+21*21 = 1127

Х^-1 – обратная матрица Х.

Обозначим выборочные наблюдения через

Х₁, Х₂, …, Х_n;

У₁, У₂, …, У_n

и введем их арифметические средние

Х = ,У = ,

где = Х₁+Х₂+ …+Х_n;

X – фактор, объясняемая переменная, влияющая на следствие У;

У – следствие, зависимая переменная.

Греческими буквами обозначают параметры модели для генеральной совокупности.

Например, ₀, ₁ – параметры линейной модели У=₀+₁X+ для генеральной совокупности,

Где  - случайное возмущение или ошибка модели, которая состоит из ошибки уравнения и ошибки измерения.

Латинскими буквами обозначают коэффициенты уравнения регрессии для выборочной совокупности.

Например, а₀, а₁ – коэффициенты уравнения регрессии У = а₀+а₁Х+е для выборочной совокупности,

где е = У - (а₀ + а₁Х) = У - У_p -– отклонение или остаток (Гаусс называл его убытком, В эконометрической литературе принято е называть остатком), учитывающий влияние всех факторов, не включенных в модель;

У – фактические значения зависимой переменной;

У_p= а₀+а₁Х - расчетные значения У;

Х – фактор.

 - белый шум.

m – число степеней свободы.

n – объем выборки.

Т – период периодического колебания.

k – количество всех коэффициентов в модели (включая свободный коэффициент).

Например, уравнение регрессии У=а₀+а₁Х + е имеет два коэффициента: а₀ и а₁, следовательно k = 2.

t – индекс времени в моделях временных рядов.

Например, У_t = a₀+a₁X_t +e_t, t – индекс времени.

t_a1 – фактическое значение критерий Стьюдента для коэффициента а₁.

Например, t_а1 = a₁/S_a1,

где S_a1 – среднее квадратическое отклонение коэффициента а₁ от своего математического ожидания ₁, или ошибка коэффициента а₁.

t_/2( = 0.05, m = n - 1) или t_/2 – двухстороннее (критическое) табличное значение критерия Стьюдента.

t_( = 0.05, m = n - 1) или t_ – одностороннее (критическое) табличное значение критерия Стьюдента,

где  - уровень значимости критерия или вероятность ошибки при отклонении верной нулевой гипотезы или вероятность совершить ошибку первого рода;

ошибка первого рода – неправильное отклонение нулевой гипотезы;

m = n - 1 – число степеней свободы для критерия Стьюдента.

Например, в уравнении регрессии У=а₀+а₁Х+е, У – зависимая переменная, Х – фактор.

В системах одновременных уравнений У может выступать как объясняемая переменная.

У ₁ = а₀+а₁Х₁+а₂У₂+ е₁,

У₂ = b₀+b₁X₂ +b₂У₁ + е₂

В первом уравнении: У₁ – зависимая переменная, Х₁ – фактор, У₂ – объясняемая переменная.

Во втором уравнении: У₂ – зависимая переменная, Х₂ – фактор, У₁ – объясняемая переменная.

Введем обозначения уравнения регрессии для трех переменных.

Предположим, мы имеем три связанные между собой переменные, которые обозначим через X₁, X₂, У. Переменная У может, например, отражать количество покупок некоторого товара в домашнем хозяйстве семьи, Х₁ – цена товара, Х₂ – доход семьи. Произведем выборку объемом n из генеральной совокупности, составляющая N семей. Численные значения переменных выборки мы будем записывать в таблице 0.1.

Таблица 0.1. - Исходные значения выборочной совокупности

i	X1	X2	У
1	X11	X21	У1
2	X12	X22	У2
i	X1i	X2i	Уi
…	…	…	…
n	X1n	X2n	Уn

Здесь Х_di обозначает величину переменной Х_d для i-го домашнего хозяйства. Гипотеза о линейной зависимости У от Х₁ и Х₂ может быть записана в виде

У_i = α₀ + α₁X_1i + α₂X_2i + _i , i = 1, 2, … , n.

Примечание. Большинство статистических пакетов предполагает предложенную схему размещения переменных в таблице базы данных: сначала размещают столбцы факторов Х_d, последним ставят столбец зависимой переменной У.

Е – ошибка модели.

F – фактическое значение критерия Фишера.

F_кр(α = 0,05; m₁ = k - 1; m₂ = n - k) – критическое значение критерия Фишера на уровне значимости α и числе степеней свободы m₁, m₂.

S – среднее квадратическое отклонение для выборочной совокупности.

S² – дисперсия для выборочной совокупности.

 - среднее квадратическое отклонение для генеральной совокупности.

² – дисперсия для генеральной совокупности.

М – условное обозначение математического ожидания.

Например. М(_i) = 0 при всех i = 1, 2, … , n.

r – коэффициент корреляции.

r² – коэффициент детерминации.

R – множественный коэффициент корреляции.

R² – множественный коэффициент детерминации.

Буквы в формулах, выделенные полужирным шрифтом, означают матрицу.

Например. В формуле

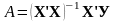
А, Х, У - матрицы.

Расчетные формулы. Расчет коэффициентов регрессионного уравнения

У = а₀ + а₁Х + е

где А - матрица коэффициентов модели; Х и У - матрицы соответственно факторов и зависимой переменной.

Ошибка модели:

где У_рi = а₀ + а₁Х_i .

Основное вариационное уравнение

где = С_общ. – вариация общая;

= С_ост – вариация остатков;

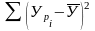
= С_рег = С_общ- С_ост – вариация регрессии.

S_общ² = - дисперсия общая.

S_оcт² = - дисперсия остатков.

S_рег²= - дисперсия регрессии.

- коэффициент детерминации.

Множественный коэффициент детерминации:

.

Критерий Фишера:

.

Ошибка коэффициента а₀:

.

Ошибка коэффициента а₁:

Критерий Стьюдента для коэффициента а₁:

.

Частный коэффициент детерминации для фактора Х₁:

где t_i - критерий Стьюдента для фактора Х_i

Точечный прогноз:

У_пр = а₀+а₁Х_ож,

где Х_ож – ожидаемое значение Х.

95% интервальный прогноз для математического ожидания У:

Р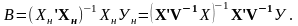 асчет коэффициентов модели методом Эйткена:

Парный коэффициент корреляции:

Частный коэффициент корреляции:

где С_ij – элементы обратной матрицы от матрицы всех парных коэффициентов корреляции.

Критическое значение коэффициента корреляции:

где t_/2 = t_/2( = 0,05; m = n - 2).

Коэффициент автокорреляции:

.

Критерий Дарбина – Уотсона (Дарбина – Ватсона):

.

Элементы математической статистики

Напомним основные правила работы с массивами чисел и основные формулы математической статистики, которые потребуются нам в дальнейшем изложении курса.

Операции суммирования

Пусть величина Х задается последовательностью данных Х₁, Х₂, … , Х_n, каждое из которых можно записать как Х_i, i = 1, , n.

Сумма этих чисел записывается следующим образом:

.

Если из текста понятно, какие начальные и конечные суммируемые члены, то можно использовать сокращенное обозначение:

.

Обозначим:

- среднее значение величины Х.

Правила суммирования (а, b – константы):

1. Σа = na.

2. ΣaХ_i = aΣХ_i = anХ.

3. Σ(a+bХ_i) = na+bnХ.

4. Σ(Х_i+У_i) = ΣХ_i + ΣУ_i = n(Х + У).

5. Σ(Х_i-Х)=0.

6. .

7. .

Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений, причем в качестве весового коэффициента берется вероятность соответствующего исхода.

Предположим, что Х может принимать n конкретных значений

(Х₁, Х₂, …, Х_n) и что вероятность получения Х_i равна p_i, тогда

М(Х) = Х₁р₁ +Х₂р₂+…+Х_np_n = ΣХ_ip_i .

Если р_i = n_i/n, i = 1, 2, …, k, где Σn_i = n, то

М(Х) = Х₁р₁ +Х₂р₂+…+Х_kp_k = (Х₁n₁ +Х₂n₂+…+Х_kn_k )/n =

= (ΣХ_in_i)/n = X.

Если n_i = 1 для каждого i= 1, 2, …, n, то

М(Х) = (Х₁ +Х₂+…+Х_n)/n = (ΣХ_i)/n = X.

Свойства математического ожидания:

(а, b – константы; Х, У – случайные величины; р – вероятность случайной величины)

1) М(а) = а;

2) М(аХ) = аМ(Х);

3) М(а+bX) = a + bM(X);

4) M(X + У) = М(Х) + М(У);

5) М(ХУ) = М(Х) М(У), при условии, что Х и У не связаны между собой;

6) математичемкое ожидание функции f(X) определяется выражением:

М(f(X)) = Σf(X_i)p_i.

Например, если f(X) = X² , то М(f(X)) = М(Х²) = ΣХ_i² p_i.

Свойства дисперсии:

* Дисперсия для генеральной совокупности

σ² = D(X)=M(X_i-X)²;

a, b – константы, Х – случайная величина

1) D(a) = 0;

2) D(aX) = a²D(X);

3) D(a+bX) = b²D(X).

* Дисперсия для выборочной совокупности

Var(X) = .

Выборочная дисперсия var(X) является смещенной оценкой генеральной дисперсии σ ², при этом

М[Var(X)] = .

В качестве несмещенной оценки генеральной дисперсии используется величина

S² =

1) Var(a) = 0;

2) Var(aX) = a²Var(X);

3) Var(a+bX) = b²Var(X).

Основные понятия регрессионного анализа

Линейная регрессионная модель. Зависимость следствия У от причины Х моделируется с помощью линейного регрессионного уравнения

У_i = a₀ + a₁X_i + e_i,

где У_i - фактическое значение товарооборота;

Х_i - фактическое значение затрат на рекламу;

i - порядковый номер измерения.

Рис. 1.2. Структура регрессионного уравнения У_i =а₀+а₁Х_i+е_i=У_рi+е_i

У_pi=a₀+a₁Х_i - расчетные значения товарооборота отражают существующую связь между У и X;

e_i = (У_i - У_pi) - остатки модели, отражают влияние неучтенных факторов;

a₁- коэффициент модели, определенный методом наименьших квадратов, численно равный приросту значения У при изменении Х на единицу.

где - ковариация или сумма произведений отклонений значений X и У от своих средних значений;

Х - среднее значение Х_i;

У - среднее значение У_i;

- вариация переменной Х или сумма квадратов отклонений

значений X от своего среднего значения;

- коэффициент модели, определенный методом наименьших квадратов, численно равный значению У_р при значении Х равном нулю.

Виды моделей:

модель распределенных лагов:

У_t = ₀ + ₁X_t + ₂X_t-1 + ₃X_t-2+ _t;

авторегрессионная модель распределенных лагов:

У_t = ₀ + ₁X_t + ₂У_t-1 + _t;

авторегрессионная модель:

У_t = ₀ + ₁У_t-1 +₂У_t-2 + _t;

модель скользящей средней:

_t= _t + _t-1 + ² _t-2 + _t ;

модель последовательных отклонений:

У_t = У_t – У_t-1, t = 2, … n;

модель периодических составляющих временного ряда:

У_t = ₀ + ₁t + ₂Sin(2t/T₁) + ₃Cos(2t/T₁) + ₄Sin(2t/T₂) + ₅Cos(2t/T₂) + … + _t, где Т₁, Т₂ периоды для сезонной и длинно периодической составляющей;

модель экспоненциально взвешенного среднего:

Z_t = У_t+  (1-)У_t-1 +  (1-)²У_t-2 +  (1-)³У_t-3 +…. =

=У_t + (1-)[У_t-1 +  (1-)У_t-2 +  (1-)²У_t-3+ …];

линейная модель с автокоррелированными возмущениями:

У_t =₀ +₁Х_t + ρ_t-1+ _t.

Прогноз по линейной модели с автокоррелированными возмущениями:

У_пр(n+1) = ₀ + ₁X_n+1 + _n.

Метод устранения гетероскедастичности:

У_i/|e_i| = a₀/|e_i| + a₁X_I/|e_i| + e_i/|e_i| .

ЛИНЕЙН – функция Ехсе1, для расчета коэффициентов и качества линейной модели.

Регрессия – программа Ехсе1 для расчета коэффициентов и качества линейной модели.